Tự luận Hình học Lớp 11 - Chương 2 - Chủ đề 6: Khoảng cách (Phần 2)

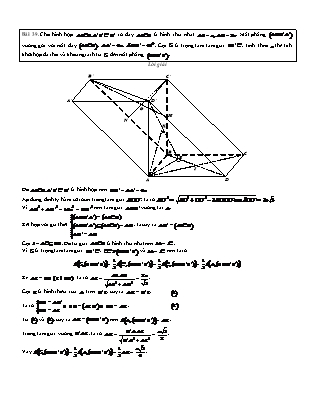
 Bài 39. Cho hình hộp ABCD.A' B'C' D' có đáy ABCD là hình chữ nhật AB = a, AD = 2a . Mặt phẳng (ADD' A') 
 · 0
vuông góc với mặt đáy (ABCD), AA' = 4a , ADD' = 60 . Gọi G là trọng tâm tam giác BB'C' . Tính theo a thể tích 
khối hộp đã cho và khoảng cách từ G đến mặt phẳng (BDD' B').
 Lời giải
 B' C'
 A' D'
 G
 M
 N
 K
 B C
 E
 I
 A D
Do ABCD.A' B'C' D' là hình hộp nên DD' = AA' = 4a .
 2 2 2 ·
Áp dụng định lý hàm số côsin trong tam giác ADD' , ta có AD' = AD + DD' - 2AD.DD'cos ADD' = 2a 3 .
Vì AD2 + AD'2 = 16a2 = DD'2 nên tam giác ADD' vuông tại A .
 ì
 ï (ADD' A')^ (ABCD)
 ï
Kết hợp với giả thiết íï (ADD' A')Ç(ABCD)= AD , ta suy ra AD' ^ (ABCD) .
 ï
 ï AD' ^ AD
 îï
Gọi I = AC ÇBD . Do tứ giác ABCD là hình chữ nhật nên IA = IC .
Vì G là trọng tâm tam giác BB'C' , CC'P(BDD' B') và IA = IC nên ta có
 1 1 1
 d(G,(BDD' B))= d(C',(BDD' B'))= d(C,(BDD' B'))= d(A,(BDD' B')).
 3 3 3
 AB.AD 2a
Kẻ AE ^ BD (E Î BD). Ta có AE = = .
 AB2 + AD2 5
Gọi K là hình chiếu của A trên D' E , suy ra AK ^ D' E . (1)
 ïì BD ^ AD'
Ta có íï Þ BD ^ (AED')Þ BD ^ AK . (2)
 îï BD ^ AE
Từ (1) và (2), suy ra AK ^ (BDD' B') nên d(A,(BDD' B'))= AK .
 D' A.AE a 3
Trong tam giác vuông D' AE , ta có AK = = .
 D' A2 + AE2 2
 1 1 a 3
Vậy d(G,(BDD' B'))= d(A,(BDD' B'))= AK = .
 3 3 6 · 0
Bài 40. Cho lăng trụ ABCD.A' B'C' D' có đáy ABCD là hình thoi cạnh a , tâm O và ABC = 120 . Góc giữa cạnh bên 
 AA' và mặt đáy bằng 600 . Đỉnh A' cách đều các điểm A , B , D . Gọi M là trung điểm cạnh CD . Tính khoảng cách 
từ điểm M đến mặt phẳng (A' BD).
 Lời giải
 · 0 · 0
 Hình thoi ABCD có ABC = 120 suy ra BAD = 60 nên tam 
 B' C'
 giác ABD là tam giác đều cạnh a .
 Gọi H là hình chiếu vuông góc của A' xuống mặt đáy 
 (ABCD). Do đỉnh A' cách đều các điểm A , B , D nên H 
 A' D' trùng với tâm đường tròn ngoại tiếp tam giác ABD . Suy ra 
 1 1 a 3 a 3
 H thuộc đoạn AO sao cho OH = AO = . = . Khi 
 3 3 2 6
 đó hình chiếu vuông góc của AA' trên mặt đáy (ABCD) là 
 0 · · ·
 HA nên 60 = AA',(ABCD)= AA',HA = A' AH .
 B C
 K Trong tam giác vuông A' AH , ta có 
 ·
 A' H = AH.tan A' AH = a .
 O M
 H
 A D Do M là trung điểm CD , O là trung điểm AC và H là tâm 
 của tam giác ABD nên
 1 1 3
 d(M,(A' BD))= d(C,(A' BD))= d(A,(A' BD))= d(H,(A' BD)).
 2 2 2
Gọi K là hình chiếu của H trên A'O , suy ra HK ^ A'O . (1)
 ïì BD ^ HO
Ta có íï Þ BD ^ (A' HO)Þ BD ^ HK . (2)
 îï BD ^ A' H
Từ (1) và (2), suy ra HK ^ (A' BD) nên d(H,(A' BD))= HK .
 A' H.OH a 13 3 3a 13
Trong tam giác vuông A' HO , ta có HK = = . Vậy d(M,(A' BD))= HK = .
 A' H2 + OH2 13 2 26
 VẤN ĐỀ 3. Khoảng cách giữa đường thẳng và mặt phẳng song song
 Khoảng cách giữa hai mặt phẳng song song
Bài 41. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với BC = a , cạnh bên SA = 2a . Hình chiếu vuông góc 
của S trên mặt đáy trùng với tâm của đáy, mặt phẳng (SBC) tạo với đáy một góc bằng 600 . Tính khoảng cách giữa 
đường thẳng BC và mặt phẳng (SAD).
 Lời giải
Gọi O = AC ÇBD . Theo giả thiết ta có SO ^ (ABCD).
Gọi M là trung điểm BC , suy ra OM ^ BC .
 ì
 ï BC ^ OM 0 · · ·
Ta có íï Þ BC ^ (SOM)Þ BC ^ SM . Do đó 60 = (SBC),(ABCD)= SM,OM = SMO .
 îï BC ^ SO
Tam giác SAC có SO vừa là trung tuyến vừa là đường cao nên cân tại S , suy ra SC = SA = 2a . Trong tam giác vuông SMC , ta có
 a 15
 SM = SC2 - MC2 = .
 2
 S Trong tam giác vuông SOM , ta có
 · 3a 5 · a 15
 SO = SM.sinSMO = ; OM = SM.cosSMO = .
 4 4
 Vì BC P(SAD) và M Î BC nên
 d(BC,(SAD))= d(M,(SAD))= 2d(O,(SAD)).
 ì
 ï ON ^ AD
 ï
 Kéo dài MO cắt AD tại N , suy ra í a 15 .
 K ï = =
 ï ON OM
 B A îï 4
 Kẻ OK ^ SE K Î SE . 1
 M ( ) ( )
 N
 O ïì AD ^ ON
 Ta có íï Þ AD ^ (SON)Þ AD ^ OK . (2)
 C D îï AD ^ SO
 Từ (1) và (2), suy ra OK ^ (SAD) nên d(O,(SAD))= OK .
 SO.ON 3a 5 3a 5
Trong tam giác vuông SON , ta có OK = = . Vậy d(BC,(SAD))= 2d(O,(SAD))= 2OK = .
 SO2 + ON2 8 4
Bài 42. Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB = 2a , cạnh bên 
 SA = a 6 và vuông góc với đáy. Tính khoảng cách từ đường thẳng AB đến mặ phẳng (SCD).
 Lời giải
Do ABCD là nửa lục giác đều nội tiếp đường tròn đường
kính AB nên ABPCD suy ra ABP(SCD). Do đó S
 d(AB,(SCD))= d(A,(SCD)).
Kẻ AE ^ CD với E thuộc đường thẳng CD .
Gọi K là hình chiếu của A trên SE , suy ra AK ^ SE . (1)
 ïì CD ^ SA
Ta có íï Þ CD ^ (SAE)Þ CD ^ AK . (2)
 îï CD ^ AE
Từ (1) và (2), suy ra AK ^ (SCD) nên d(A,(SCD))= AK .
Goi O là trung điểm AB , suy ra tam giác OAD đều cạnh a . K
 I O
 a 3 A B
Hạ DI ^ AO (I Î AO), suy ra DI = .
 2
Trong tam giác vuông SAE , ta có 
 SA.AE SA.DI a 6
 AK = = = .
 SA2 + AE2 SA2 + DI2 3 E D C
 a 6
Vậy d(AB,(SCD))= d(A,(SCD))= AK = .
 3
Bài 43. Cho lăng trụ đứng ABC.A' B'C' có đáy ABC là tam giác vuông có BA = BC = a , cạnh bên AA' = a 2 . Gọi M 
là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng AM và B'C .
 Lời giải A' C'
Gọi E là trung điểm của BB' .
Ta có EM PB'C suy ra B'C P(AEM). Do đó 
 B'
 d(B'C, AM)= d(B'C,(AEM))= d(C,(AEM))= d(B,(AEM)).
Nhận xét tứ diện EABM có BA, BE, BM đôi một vuông góc nên 
 1 1 1 1
 = + +
 d2 (B,(AEM)) BA2 BE2 BM2 E
 1 2 4 7
 = + + = . A C
 a2 a2 a2 a2
 a 7 M
Vậy d(B'C, AM)= d(B,(AEM))= .
 7 B
 VẤN ĐỀ 4. Khoảng cách giữa hai đường thẳng chéo nhau
Bài 44. Cho hình chóp S.ABC có đáy ABC là tam giác vuông với AB = BC = a , cạnh bên SA = 2a và vuông góc với 
đáy. Gọi M là trung điểm AC . Tính khoảng cách giữa hai đường thẳng SM và BC .
 Lời giải
 S Gọi N là trung điểm AB , suy ra BC PMN nên BC P(SMN).
 Do đó
 d(BC,SM)= d(BC,(SMN))= d(B,(SMN))= d(A,(SMN)).
 Kẻ AK ^ SN (K Î SN). (1)
 Vì BC PMN mà BC ^ AB nên MN ^ AB .
 ïì MN ^ AB
 Ta có íï Þ MN ^ (SAB)Þ MN ^ AK . (2)
 îï MN ^ SA
 K Từ (1) và (2), suy ra AK ^ (SMN) nên d(A,(SMN))= AK .
 A M C
 Trong tam giác vuông SAN , ta có 
 SA.AN 2a 17
 = =
 N AK .
 SA2 + AN2 17
 2a 17
 B Vậy d(BC,SM)= d(A,(SMN))= AK = .
 17
 B =
Bài 45. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại với AC 2a 2 . Hai mặt phẳng (SAB) và 
 (SAC) cùng vuông góc với đáy, mặt phẳng (SBC) tạo với đáy một góc 600 . Gọi M là trung điểm AC . Tính khoảng 
cách giữa hai đường thẳng AB và SM .
 Lời giải
Do hai mặt phẳng (SAB) và (SAC) cắt nhau theo giao tuyến SA và cùng vuông góc với đáy (ABC) nên SA ^ (ABC).
 ïì BC ^ AB
Ta có íï Þ BC ^ (B)Þ BC ^ SB .
 îï BC ^ SA (SBC)Ç(ABC)= BC ïü
 ï
 ï 0 · · ·
Do SB Ì (SBC),SB ^ BC ýï suy ra 60 = (SBC),(ABC)= SB, AB = SBA .
 ï
 Ì ^ ï
 AB (ABC), AB BCþï
 AC
 Vì tam giác ABC vuông cân tại B nên AB = BC = = 2a .
 S 2
 ·
 Trong tam giác vuông SAB , ta có SA = AB.tanSBA = 2a 3 .
 Gọi N là trung điểm BC , suy ra ABPMN nên ABP(SMN).
 Do đó
 d(AB,SM)= d(AB,(SMN))= d(A,(SMN)).
 Gọi E là hình chiếu vuông góc của A trên đường thẳng 
 K MN . Khi đó tứ giác ABNE là hình chữ nhật nên 
 BC
 AE = BN = = a .
 E 2
 Kẻ AK ^ SE K Î SE . 1
 A M C ( ) ( )
 ïì MN ^ AE
 Ta có íï Þ MN ^ SAE Þ MN ^ AK . 2
 N ( ) ( )
 îï MN ^ SA
 B Từ (1) và (2), suy ra AK ^ (SMN) nên d(A,(SMN))= AK .
 SA.AE 2a 39 2a 39
Trong tam giác vuông SAE , ta có AK = = . Vậy d(AB,SM)= d(A,(SMN))= AK = .
 SA2 + AE2 13 13
Bài 46. Cho tứ diện ABCD có ABC là tam giác vuông tại A , AB a , AC a 3 , DA DB DC . Tính khoảng cách 
giữa hai đường thẳng AD và BC , biết tam giác DBC vuông.
 Lời giải
Gọi H là trung điểm BC , suy ra H là tâm đường tròn D
ngoại tiếp tam giác ABC nên HA = HB = HC . Mặt khác, 
 DA DB DC suy ra DH là trục của đường tròn ngoại 
tiếp tam giác ABC . Do đó DH ^ (ABC).
Kẻ Ax PBC . Khi đó 
 d AD,BC d BC, ADx d H, ADx .
 K
Gọi E là hình chiếu của H trên Ax , suy ra HE ^ Ax .
 x
Kẻ HK ^ DE (K Î DE). (1) E
 A C
 ïì Ax ^ HE
Ta có íï Þ Ax ^ (DHE)Þ Ax ^ HK . (2)
 ï Ax ^ DH
 îï H
 F
Từ (1) và (2), suy ra HK ^ (ADx) nên d H, ADx HK . B
 BC
Ta có BC AB2 AC 2 2a . Tam giác BDC vuông tại D nên DH a .
 2
 AB.AC a 3
Gọi F là chân đường cao hạ từ A của tam giác ABC , suy ra HE AF 
 BC 2
 DH.HE a 21 a 21
Trong tam giác vuông DHE , ta có HK . Vậy d AD,BC d H, ADx HK .
 DH 2 HE2 7 7 Bài 47. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BC a , AC 2a ; tam giác SAB đều. Hình chiếu 
vuông góc của đỉnh S trên mặt đáy trùng với trung điểm M của AC . Tính khoảng cách giữa hai đường thẳng SA và 
 BC .
 Lời giải
 Kẻ Ax PBC . Khi đó
 S
 d SA,BC d BC, SAx d C, SAx 2d M, SAx .
 Gọi E là hình chiếu của M trên Ax , suy ra ME ^ Ax .
 Kẻ MK  SE K SE . 1 
 Ax  ME
 Ta có Ax  SME Ax  MK . 2 
 Ax  SM
 K x
 Từ 1 và 2 , suy ra MK  SAx nên d M, SAx MK .
 E
 A C Tam giác SAB đều nên SA SB AB AC 2 BC 2 a 3 .
 M
 Trong tam giác vuông SMA , ta có SM SA2 AM 2 a 2 .
 AB a 3
 B Ta có ME AM.sin E· AM AM.sin A· CB AM. .
 AC 2
 SM.ME a 66 2a 66
Trong tam giác vuông SME , ta có MK . Vậy d SA,BC 2d M, SAx 2MK .
 SM 2 ME2 11 11
Bài 48. Cho tứ diện đều ABCD cạnh a . Gọi M , N lần lượt là trung điểm của AB và CD . Tính khoảng cách giữa hai 
đường thẳng BN và CM .
 Lời giải
Gọi H là tâm của tam giác đều BCD thì AH ^ (BCD).
 A
Goi P là trung điểm AN , suy ra MP PBN . Từ C kẻ đường 
thẳng Cx song song với BN , hạ BQ ^ Cx tại Q . Khi đó CM , 
 MP , CQ cùng thuộc một mặt phẳng chứa CM và song song với 
 BN . Do đó
 M
 L
 d(BN,CM)= d(BN,(MPCQ))= d(H,(MPCQ)). P
Gọi L = MP Ç AH , E là hình chiếu của H trên CQ .
Kẻ HK ^ LE (K Î LE). 1 
 B D
 ïì CQ ^ HE
Ta có íï Þ CQ ^ (AHE)Þ CQ ^ HK . 2 
 ï ^ K
 îï CQ AH Q H
 N
Từ 1 và 2 , suy ra HK  MPCQ nên d H, MPCQ HK .
 E
 C
 · 0 a
Ta có HE = BQ = BC cosQBC = acos60 = ;
 2
 AH AB2 - BH2 a 6
 LH = = = .
 2 2 6
 LH.HE a 10 a 10
Trong tam giác vuông LHE , ta có HK . Vậy d(BN,CM)= d(H,(MPCQ))= HK = .
 LH 2 HE2 10 10 Bài 49. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và AB = a, AC = a 3 ; SA = 2a và vuông góc với 
đáy. Gọi M là trung điểm SB . Tính khoảng cách giữa hai đường thẳng AM và BC .
 Lời giải
 Gọi H là hình chiếu của A lên đường thẳng BC .
 ì
 ï BC ^ AH
 S Ta có í Þ BC ^ (SAH).
 îï BC ^ SA
 Gọi N là trung điểm SC , suy ra MN PBC . Do đó 
 d(BC, AM)= d(BC,(AMN))= d(B,(AMN))= d(S,(AMN)).
 K Gọi E = SH ÇMN . Kẻ SK ^ AE (K Î AE). 1 
 N
 ì
 ï MN PBC
 Ta có í Þ MN ^ (SAH)Þ MN ^ SK . 2 
 ï ^
 M E îï BC (SAH)
 Từ 1 và 2 , suy ra SK  AMN nên d(S,(AMN))= SK .
 2 2
 A C Trong tam giác vuông ABC , ta có BC = AB + AC = 2a ; 
 AB.AC a 3 AB2 a BH a
 AH = = ; BH = = suy ra ME = = .
 BC 2 BC 2 2 4
 H SB SA2 + AB2 a 5
 Ta có AM = = = . Tam giác AEM 
 B 2 2 2
 a 19
 vuông tại E nên AE = AM2 - ME2 = .
 4
Diện tích tam giác SAE được tính 
 1 S 1
 SA.AH = DSAH = S = AE.SK
 4 2 DSAE 2
 SA.AH 2a 3 2a 3
suy ra SK = = . Vậy d(BC, AM)= d(S,(AMN))= SK = .
 2AE 19 19
Bài 50. Cho tứ diện ABCD có AB = CD = a, AC = BD = b, AD = BC = c . Tính khoảng cách giữa hai đường thẳng AB 
và CD .
 Lời giải
Gọi M , N lần lượt là trung điểm cạnh AB và CD . Ta có A
 CA2 + CB2 CD2 b2 + c2 a2
 CM2 = - = - ;
 2 4 2 4
 AD2 + DB2 AB2 b2 + c2 a2
 DM2 = - = - .
 2 4 2 4 M
Suy ra CM = DM nên tam giác CMD cân tại M và có 
trung tuyến MN , do đó MN ^ CD .
Tương tự, ta cũng có NM ^ AB . Vậy d(AB,CD)= MN .
Trong tam giác vuông MNC , ta có B D
 b2 + c2 a2 a2 b2 + c2 - a2
 MN2 = CM2 - CN2 = - - = .
 2 4 4 2
 N
 b2 + c2 - a2
Vậy d(AB,CD)= MN = .
 2 C Bài 51. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh bên SA = a 3 và vuông góc với đáy. 
Gọi M là trung điểm của SD . Tính khoảng cách giữa hai đường thẳng AM và SB .
 Lời giải
 S Gọi O = AC ÇBD , suy ra MO PSB . Do đó
 d(SB, AM)= d(SB,(AMO))= d(S,(AMO))= d(D,(AMO)).
 Gọi I là trung điểm AD , suy ra MI PSA nên MI ^ (ABCD). 
 M Khi đó 
 d(SB, AM)= d(D,(AMO))= 2d(I,(AMO)).
 Gọi E là hình chiếu của I trên AC , suy ra IE ^ AC .
 K Kẻ IK ^ ME (K Î ME). 1 
 A I D ïì AC ^ IE
 Ta có íï Þ AC ^ (MIE)Þ AC ^ IK . 2 
 îï AC ^ MI
 E
 Từ 1 và 2 , suy ra IK  AMO nên d(I,(AMO))= IK .
 O
 SA a 3 DO a 2
 Ta có MI = = ; IE = = .
 B C 2 2 2 4
 MI.IE a 21 a 21
Trong tam giác vuông MIE , ta có IK = = . Vậy d(SB, AM)= 2d(I,(AMO))= 2IK = .
 MI2 + IE2 14 7
Bài 52. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAD đều và nằm trong mặt phẳng 
vuông góc với đáy.
 a) Tính khoảng cách giữa hai đường thẳng AD và SB .
 b) Tính khoảng cách giữa hai đường thẳng SA và BD .
 Lời giải
Gọi M là trung điểm AD , suy ra SM ^ AD . S
Mà (SAD)^ (ABCD) theo giao tuyến AD nên SM ^ (ABCD).
a) Do BC PAD nên AD P(SBC). Khi đó 
 d(AD,SB)= d(AD,(SBC))= d(M,(SBC)).
Gọi N là trung điểm BC , suy ra MN = AB = a và MN ^ BC .
Kẻ MK ^ SN (K Î SN). 1 K
 ïì BC ^ MN G D C
Ta có íï Þ BC ^ (SMN)Þ BC ^ MK . 2 
 îï BC ^ SM F
 H
Từ 1 và 2 , suy ra MK  SBC nên d(M,(SBC))= MK .
 M O N
 AD 3 a 3
Ta có SM là đường cao trong tam giác đều nên SM = = . E
 2 2
 A B
 SM.MN a 21
Trong tam giác vuông SMN , ta có MK = = .
 SM2 + MN2 7
 a 21
Vậy d(AD,SB)= d(M,(SBC))= MK = .
 7
b) Trong mặt phẳng (ABCD) lấy điểm G sao cho ABDG là hình bình hành, suy ra AG PBD nên BD P(SAG). Khi đó d(BD,SA)= d(BD,(SAG))= d(D,(SAG))= 2d(M,(SAG)).
 AO a 2
Gọi E , F lần lượt là hình chiếu của M trên AG và BD . Ta có ME = MF = = .
 2 4
Kẻ MH ^ SE (H Î SE). 3 
 ïì AG ^ ME
Ta có íï Þ AG ^ (SME)Þ AG ^ MH . 4 
 îï AG ^ SM
Từ 3 và 4 , suy ra MH  SAG nên d(M,(SAG))= MH .
 SM.ME a 21 a 21
Trong tam giác vuông SME , ta có MH = = . Vậy d(BD,SA)= 2d(M,(SAG))= 2MH = .
 SM2 + ME2 14 7
Bài 53. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a . Gọi M , N lần lượt là trung điểm AD và DC . 
Hai mặt phẳng (SMC) và (SNB) cùng vuông góc với đáy, SB hợp với đáy một góc bằng 600 . Tính khoảng cách giữa 
hai đường thẳng CM và SB .
 Lời giải
Gọi H = CM ÇBN . Ta có (SMC)Ç(SNB)= SH . Mà (SMC) và (SNB) vuông góc với (ABCD) nên SH ^ (ABCD).
Do đó hình chiếu vuông góc của SB trên (ABCD) là HB nên
 0 · · ·
 60 = SB,(ABCD)= SB,HB = SBH .
 · · · · 0 · · 0
Ta có DCMD = DBNC (c - c - c), suy ra CMD = BNC . Mà CMD + DCM = 90 nên BNC + DCM = 90 .
 · 0
Suy ra CHN = 90 hay CM ^ BN .
 BC2 4a
 Ta có BN = BC2 + NC2 = a 5 , suy ra BH = = , 
 S BN 5
 · 4a 3
 SH = BH.tanSBH = .
 5
 a) Gọi K là hình chiếu của H trên SB , suy ra HK ^ SB . 1 
 ïì MC ^ BN
 Ta có íï Þ MC ^ (SHB)Þ MC ^ HK . 2 
 îï MC ^ SH
 D M A Từ 1 và 2 , suy ra d(CM,SB)= HK .
 K Trong tam giác vuông SHB , ta có 
 N SH.HB 2a 15
 HK = = .
 H SH2 + HB2 5
 2a 15
 C B Vậy d(CM,SB)= HK = .
 5
Bài 54. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi M , N lần lượt là trung điểm AD và DC . 
Hai đường thẳng CM và BN cắt nhau tại H , SH = a 3 và vuông góc với đáy. Tính khoảng cách giữa hai đường 
thẳng AN và SB .
 Lời giải · ·
Ta có DCMD = DBNC (c - c - c), suy ra CMD = BNC . S
 · · 0 · · 0
Mà CMD + DCM = 90 nên BNC + DCM = 90 .
 · 0
Suy ra CHN = 90 hay CM ^ BN .
Gọi P là điểm đối xứng của N qua C . Khi đó ABPN là
hình bình hành nên AN PBP suy ra AN P(SBP). Do đó
 d(AN,SB)= d(AN,(SBP))= d(N,(SBP))
 D M A
 NB 5
 = .d(H,(SBP))= d(H,(SBP)).
 HB 4
 N
Gọi E , F lần lượt là hình chiếu của H và N trên BP . L
Kẻ HL ^ SE (L Î SE). 1 H
 ïì BP ^ HE C
Ta có íï Þ BP ^ (SHE)Þ BP ^ HL . 2 B
 îï BP ^ SH
 F E
Từ 1 và 2 , suy ra HL  SBP nên d(H,(SBP))= HL .
 P
 1 1 NP.BC AB.BC 2a
Ta có SDBNP = NP.BC = BP.NF suy ra NF = = = .
 2 2 BP BN 5
 HE BH 4 4NF 8a
Vì = = suy ra HE = = .
 NF BN 5 5 5 5
 SH.HE 24a 5 5 30a
Trong tam giác vuông SHE , ta có HL = = . Vậy d(AN,SB)= d(H,(SBP))= HL = .
 SH2 + HE2 1317 4 4 1317
Bài 55. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a . Gọi E là điểm đối xứng của D qua 
trung điểm của SA , M là trung điểm của AE , N là trung điểm của BC . Tính khoảng cách giữa hai đường thẳng 
 MN và AC .
 Lời giải
 E S
 Gọi P là trung điểm của SA . Suy ra MP là đường trung 
 bình của tam giác EAD nên MP song song và bằng một nửa 
 AD . Do đó tứ giác MNCP là hình hình hành.
 Suy ra MN PPC nên MN P(SAC). Khi đó
 M P
 1
 d(MN, AC)= d(MN,(SAC))= d(N,(SAC))= d(B,(SAC)).
 2
 ì
 ï BO ^ AC
 A D Ta có í Þ BO ^ (SAC) nên d(B,(SAC))= BO .
 îï BO ^ SO
 1 1 1 a 2
 O Vậy d(MN, AC)= d(B,(SAC))= BO = BD = .
 2 2 4 4
 B N C
Bài 56. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a , AD a 2 . Gọi H là trung điểm cạnh 
 AB , tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa mặt phẳng SAC và đáy ABCD 
bằng 600 . Tính khoảng cách giữa hai đường thẳng CH và SD .
 Lời giải