Tự luận Hình học Lớp 11 - Chương 2 - Chủ đề 6: Khoảng cách (Phần 1)

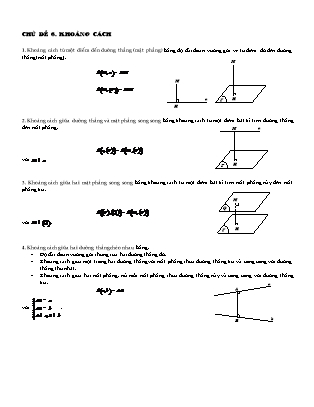
 CHUÛ ÑEÀ 6. KHOAÛNG CAÙCH
1. Khoảng cách từ một điểm đến đường thẳng (mặt phẳng) bằng độ dài đoạn vuông góc vẽ từ điểm đó đến đường 
thẳng (mặt phẳng).
 M
 d(M,a)= MH
 M
 d(M,(P))= MH
 a P H
 H
2. Khoảng cách giữa đường thẳng và mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên đường thẳng 
đến mặt phẳng. M a
 d(a,(P))= d(M,(P))
với M Î a .
 P H
3. Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kì trên mặt phẳng này đến mặt 
phẳng kia.
 M
 Q
 d((P),(Q))= d(M,(P))
với M Î (Q).
 P H
4. Khoảng cách giữa hai đường thẳng chéo nhau bằng:
 Độ dài đoạn vuông góc chung của hai đường thẳng đó.
 Khoảng cách giữa một trong hai đường thẳng với mặt phẳng chứa đường thẳng kia và song song với đường 
 thẳng thứ nhất.
 Khoảng cách giữa hai mặt phẳng, mà mỗi mặt phẳng chứa đường thẳng này và song song với đường thẳng 
 kia. a
 d(a,b)= AB A
 ïì AB ^ a
 ï
với íï AB ^ b .
 ï
 ï A Î a,B Î b
 îï B b VẤN ĐỀ 1. Khoảng cách từ một điểm đến một đường thẳng
Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a ; SA = a và vuông góc với đáy. Gọi I, M 
theo thứ tự là trung điểm của SC, AB . Tính khoảng cách từ I đến đường thẳng CM , từ đó suy ra khoảng cách từ S 
đến CM .
 Lời giải
 Ta có IO là đường trung bình của DSAC nên IO PSA .
 Mà SA ^ ABCD suy ra IO ^ ABCD nên IO ^ CM . 1 
 S ( ) ( ) ( )
 Kẻ OH ^ CM (H Î CM). (2)
 Từ (1) và (2), suy ra CM ^ (IOH)Þ CM ^ IH . Do đó 
 d(I,CM)= IH .
 Gọi K = CM ÇBO suy ra K là trọng tâm tam giác ABC nên 
 BO a 2
 I OK = = . Trong tam giác vuông KOC , ta có
 3 6
 OK.OC a
 = =
 A OH .
 D OK2 + OC2 20
 M Trong tam giác vuông IOH , ta có
 K
 O 2
 æSAö a 30
 H IH = IO2 + OH2 = ç ÷ + OH2 = .
 èç ø÷
 B C 2 10
 a 30
 Vậy d(I,CM)= IH = .
 10
 d(S,CM) SC a 30
Vì SI ÇCM = C nên = = 2 suy ra d(S,CM)= 2.d(I,CM)= .
 d(I,CM) IC 5
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , AB BC a , AD 2a . Cạnh bên SA 
vuông góc với đáy và SA a 2 . Tính khoảng cách từ B đến đường thẳng SD .
 Lời giải
Trong tam giác SBD , kẻ BH ^ SD . Khi đó S
 d(B,SD)= BH .
 H
Ta có SB = SA2 + AB2 = a 3 ; SD = SA2 + AD2 = a 6 ;
 BD = AB2 + AD2 = a 5 .
 2 2 2
 · SB + SD - BD 2 · 7
Suy ra cos BSD = = nên sin BSD = .
 2SB.SD 3 3
 1 · 1
Ta có S = SB.SD.sin BSD = SD.BH suy ra A D
 DSBD 2 2
 · a 21
 BH = SB.sin BSD = .
 3
 a 21
Vậy d(B,SD)= BH = . B C
 3 VẤN ĐỀ 2. Khoảng cách từ một điểm đến một mặt phẳng
Bài 3. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , mặt bên tạo với đáy một góc 300 . Tính khoảng cách từ 
điểm A đến mặt phẳng (SBC).
 Lời giải
 Gọi M, N lần lượt là trung điểm AC và BC . Suy ra 
 S
 H = AN ÇBM là tâm của tam giác đều ABC . Vì S.ABC là 
 hình chóp đều nên SH ^ (ABC).
 Ta có 
 d(A,(SBC))= 3d(H,(SBC)).
 Kẻ HK ^ SN (K Î SN). (1)
 ì
 ï BC ^ HN
 M Ta có í Þ BC ^ (SHN)Þ BC ^ HK . (2)
 A C ï BC ^ SH
 K îï
 H Từ (1) và (2), suy ra HK ^ (SBC) nên d(H,(SBC))= HK .
 N
 ïì BC ^ AN
 Vì íï Þ BC ^ (SAN)Þ BC ^ SN .
 B îï BC ^ SH
 ïì (SBC)Ç(ABC)= BC
 ï
 ï 0 · · · ·
Do íï SN Ì (SBC), SN ^ BC suy ra 30 = (SBC),(ABC)= SN, AN = SNA = SNH .
 ï
 ï Ì ^
 îï AN (ABC), AN BC
 AN a 3 · a
Trong tam giác vuông SHN , ta có HN = = suy ra SH = HN.tanSNH = .
 3 6 6
 SH.HN a 3
Trong tam giác vuông SHN , ta có HK = = . 
 SH2 + HN2 12
 a 3
Vậy d(A,(SBC))= 3HK = .
 4
Bài 4. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , tam giác SAC cân tại S và nằm trong mặt phẳng 
 · 0
vuông góc với đáy, góc SBC bằng 60 . Tính khoảng cách từ A đến mặt phẳng (SBC).
 Lời giải
 S
Gọi H là trung điểm AC , suy ra SH ^ AC .
Mà (SAC)^ (ABC) theo giao tuyến AC nên SH ^ (ABC).
Ta có 
 d(A,(SBC))= 2d(H,(SBC)).
 AM a 3
Kẻ HE ^ BC (E Î BC). Ta có HE = =
 2 4
(với M là trung điểm BC ). A B
Gọi K là hình chiếu của H trên SE , suy ra HK ^ SE . (1) K
 ïì BC ^ HE
Ta có íï Þ BC ^ (SHE)Þ BC ^ HK . (2) H M
 îï BC ^ SH E
 C Từ (1) và (2), suy ra HK ^ (SBC) nên d(H,(SBC))= HK .
 a2 3a2
Đặt SH = x > 0 . Ta có SC = SH2 + HC2 = x2 + ; SB = SH2 + HB2 = x2 + .
 4 4
 2 2 2
 · SB + BC - SC a 6
Áp dụng định lý hàm số cosin trong tam giác SBC , ta có cosSBC = suy ra x = .
 2SB.SC 2
 SH.HE a 6
Trong tam giác vuông SHE , ta có HK = = .
 SH2 + HE2 6
 a 6
Vậy d(A,(SBC))= 2HK = .
 3
Bài 5. Cho hình chóp S.ABC có góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600 , các tam giác ABC và SBC là tam 
giác đều cạnh a . Tính khoảng cách từ điểm B đến mặt phẳng mặt phẳng (SAC).
 Lời giải
 Gọi M, N lần lượt là trung điểm của SA và BC .
 ïì SN ^ BC a 3
 ï = =
 S Suy ra í và SN AN .
 îï AN ^ BC 2
 Kẻ BH ^ CM (H Î CM). (*)
 Tam giác SCA cân tại C nên SA ^ CM . (1)
 M
 Tam giác SNA cân tại N nên SA ^ MN . (2)
 Từ (1) và (2), suy ra SA ^ (BCM)Þ SA ^ BH . (* *)
 B A Từ (*) và (* *), suy ra BH ^ (SAC) nên 
 d(B,(SAC))= BH .
 H ì
 N ï (SBC)Ç(ABC)= BC
 ï
 Do íï SN Ì (SBC), SN ^ BC suy ra 
 ï
 C ï Ì ^
 îï AN (ABC), AN BC
 0 · · ·
 60 = (SBC),(ABC)= SN, AN = SNA .
 SN 3 3a
Do đó tam giác SNA đều nên MN = = . 
 2 4
 1 1 MN.BC MN.BC 3 13a
Ta có SDBCM = BH.CM = MN.BC suy ra BH = = = .
 2 2 CM CA2 - AM2 13
 3 13a
Vậy d(B,(SAC))= BH = .
 13
 · 0
Bài 6. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BAC = 60 ; SA = AC = a và vuông góc với đáy. 
 a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
 b) Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
 Lời giải · a
 a) Trong tam giác vuông ABC , ta có AB = AC.cos BAC = .
 2
 Kẻ AH ^ SB (H Î SB). (1)
 S
 ïì BC ^ AB
 Ta có íï Þ BC ^ (SAB)Þ BC ^ AH . (2)
 îï BC ^ SA
 Từ (1) và (2), suy ra AH ^ (SBC). Do đó
 d(A,(SBC))= AH .
 SA.AB a 5
 Trong tam giác vuông SAB , ta có AH = = .
 SA2 + AB2 5
 H
 K
 A C a 5
 Vậy d(A,(SBC))= AH = .
 5
 ïì BK ^ AC
 b) Kẻ BK ^ AC (K Î AC). Ta có íï Þ BK ^ (SAC) .
 îï BK ^ SA
 B Do đó
 d(B,(SAC))= BK .
 · a 3 AB.BC a 3
Trong tam giác vuông ABC , ta có BC = AC.sin BAC = suy ra BK = = .
 2 AB2 + BC2 4
 a 3
Vậy d(B,(SAC))= BK = .
 4
Bài 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , BA = 3a, BC = 4a . Mặt phẳng (SBC) vuông góc 
 · 0
với đáy và SB = 2a 3 , SBC = 30 . Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
 Lời giải
Gọi H là hình chiếu vuông góc của S trên BC , suy ra SH ^ BC . S
Mà (SBC)^ (ABC) theo giao tuyến BC nên SH ^ (ABC).
 · ·
Trong tam giác vuông SHB , ta có BH = SB.cosSBH = SB.cosSBC = 3a .
 BC
Ta có d(B,(SAC))= .d(H,(SAC))= 4d(H,(SAC)).
 HC
Gọi F , E lần lượt là hình chiếu vuông góc của B và H trên AC .
Kẻ HK ^ SE (K Î SE). (1)
 ïì AC ^ HE K
Ta có íï Þ AC ^ (SHE)Þ AC ^ HK . (2)
 ï AC ^ SH B C
 îï H
Từ (1) và (2), suy ra HK ^ (SAC). Do đó d(H,(SAC))= HK . E
 BA.BC 12a HE CH 1 BF 3a
Ta có BF = = ; = = suy ra HE = = .
 BA2 + BC2 5 BF CB 4 4 5 F
 SH.HE SB2 - BH2 .HE 3a
Trong tam giác vuông SHE , ta có HK = = = . A
 SH2 + HE2 SB2 - BH2 + HE2 2 7
 6a
Vậy d(B,(SAC))= 4d(H,(SAC))= 4HK = .
 7 · 0
Bài 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , ABC = 30 ; tam giác SBC là tam giác đều cạnh a 
và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách từ điểm C đến mặt phẳng (SAB).
 Lời giải
 Gọi H là trung điểm BC , suy ra SH ^ BC .
 S Mà (SBC)^ (ABC) theo giao tuyến BC nên SH ^ (ABC).
 Ta có 
 d(C,(SAB))= 2d(H,(SAB)).
 Gọi E là trung điểm AB , suy ra HE / /AC nên HE ^ AB .
 Kẻ HK ^ SE (K Î SE). (1)
 ïì AB ^ HE
 Ta có íï Þ AB ^ (SHE)Þ AB ^ HK . (2)
 îï AB ^ SH
 Từ (1) và (2), suy ra HK ^ (SAB). Do đó 
 K
 d H, SAB = HK .
 C B ( ( ))
 H ·
 a 3 AC BC.sin ABC a
 Ta có SH = ; HE = = = .
 2 2 2 4
 E
 Trong tam giác vuông SHE , ta có 
 SH.HE a 39
 A HK = = .
 SH2 + HE2 26
 a 39
 Vậy d(C,(SAB))= 2d(H,(SAB))= 2HK = .
 13
Bài 9. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC = 2a ; SA = a và vuông góc với đáy. Tính 
khoảng cách từ trung điểm điểm I của AC đến mặt phẳng (SBC).
 Lời giải
 1
Ta có d(I,(SBC))= d(A,(SBC)). S
 2
Kẻ AH ^ SB (H Î SB). (1)
 ïì BC ^ AB
Ta có íï Þ BC ^ (SAB)Þ BC ^ AH . (2)
 îï BC ^ SA
Từ (1) và (2), suy ra AH ^ (SBC). Do đó
 d(A,(SBC))= AH .
 H
Tam giác vuông cân ABC tại B có AC = 2a , suy ra AB = a 2 . I
 A C
 SA.AB a 6
Trong tam giác vuông SAB , ta có AH = = .
 SA2 + AB2 3
 1 1 a 6
Vậy d(I,(SBC))= d(A,(SBC))= AH = .
 2 2 6 B Bài 10. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C , cạnh huyền bằng 3a . Hình chiếu vuông góc 
 a 14
của S xuống mặt đáy trùng với trọng tâm của tam giác ABC và SB = . Tính khoảng cách từ điểm B đến mặt 
 2
phẳng (SAC).
 Lời giải
 S Gọi M, N lần lượt là trung điểm AB, AC .
 Suy ra G = CM ÇBN là trọng tâm tam giác ABC .
 Theo giả thiết, ta có SG ^ (ABC).
 Ta có d(B,(SAC))= 3d(G,(SAC)).
 Kẻ GE ^ AC (E Î AC).
 Gọi K là hình chiếu của G trên SE , suy ra GK ^ SE . (1)
 ïì AC ^ GE
 Ta có íï Þ AC ^ (SGE)Þ AC ^ GK . (2)
 îï AC ^ SG
 M B
 A ^ =
 K Từ (1) và (2), suy ra GK (SAC) nên d(G,(SAC)) GK .
 G Tam giác ABC vuông cân tại C , suy ra 
 N
 AB 3a
 E CA = CB = = và CM ^ AB .
 2 2
 1 C3a 1 a a 10
Ta có CM = AB = , suy ra GM = CM = ; BG = BM2 + GM2 = ; SG = SB2 + GB2 = a .
 2 2 3 2 2
 GE NG 1 BC a
Do GE ^ AC suy ra GE / /BC . Ta có = = suy ra GE = = .
 BC NB 3 3 2
 SG.GE a
Trong tam giác vuông SGE , ta có GK = = .
 SG2 + GE2 3
Vậy d(B,(SAC))= 3d(G,(SAC))= 3GK = a 3 .
Bài 11. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A , AB = a 2 . Gọi I là trung điểm của BC , 
 uur uur
hình chiếu vuông góc H của S trên mặt đáy (ABC) thỏa mãn IA = - 2IH . Tính khoảng cách từ trung điểm K của 
 SB đến mặt phẳng (SAH).
 Lời giải
   S
Do IA 2IH . Suy ra H thuộc tia đối của tia IA và IA 2IH .
Ta có
 1
 d K, SAH d B, SAH . K
 2
 BI  AH
Vì BI  SAH nên d B, SAH BI .
 BI  SH
 A B
Tam giác ABC vuông cân tại A , suy ra BC AB 2 2a .
 1 1 a
Vậy d K, SAH d B, SAH BI .
 2 2 4 I
 H
 C · 0 · 0 · 0
Bài 12. Cho hình chóp S.ABC có ASB = 90 , BSC = 60 , ASC = 120 và SA = SB = SC = a . Tính khoảng cách từ điểm 
 S đến mặt phẳng (ABC).
 Lời giải
 S
Tam giác SAB vuông cân tại S nên AB = SA 2 = a 2 .
Tam giác SBC đều nên BC = SB = a .
Áp dụng định lí hàm số côsin trong tam giác SAC , ta có
 2 2 ·
 AC = SA + SC - 2SA.SC.cos ASC = a 3 .
Nhận xét rằng AB2 + BC2 = 2a2 + a2 = AC2 nên tam giác 
ABC vuông tại B . 
Gọi I là trung điểm AC suy ra I là tâm đường tròn ngoại tiếp 
tam giác ABC nên IA = IB = IC . Theo giả thiết SA = SB = SC , 
nên SI là trục của đường tròn ngoại tiếp tam giác ABC . Suy ra A C
 I
SI ^ (ABC). Do đó d(S,(ABC))= SI .
 SA2 + SC2 AC2 a
Trong tam giác SAC , ta có SI = - = .
 2 4 2
 a
Vậy d(S,(ABC))= SI = .
 2 B
Bài 13. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , SA = a và vuông góc với đáy, tam giác SBC cân 
tại S và tạo với đáy một góc 450 . Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
 Lời giải
 S
 Tam giác SBC cân tại S nên SB = SC .
 Suy ra DSAB = DSAC (cạnh huyền – cạnh góc vuông).
 Do đó AB = AC . Vậy tam giác ABC vuông cân tại A .
 Gọi E là trung điểm BC , suy ra AE ^ BC .
 Gọi K là hình chiếu của A trên SE , suy ra AK ^ SE . (1)
 ïì BC ^ AE
 Ta có íï Þ BC ^ (SAE)Þ BC ^ AK . (2)
 ï
 K îï BC ^ SA
 Từ (1) và (2), suy ra AK ^ (SBC) nên d(A,(SBC))= AK .
 A C
 ü
 (SBC)Ç(ABC)= BC ï
 ï
 Ta có SE Ì (SBC),SE ^ BC ýï
 E ï
 Ì ^ ï
 AE (ABC), AE BCþï
 · · · 0
 Þ (SBC),(ABC)= SE, AE = SEA = 45 .
 B
 · 0 SE SA 2 a 2
Tam gác SAE vuông tại A có SEA = 45 nên là tam giác vuông cân, suy ra AK = = = .
 2 2 2
 a 2
Vậy d(A,(SBC))= AK = .
 2 · 0
Bài 14. Cho hình chóp S.ABC có đáy là tam giác ABC với AB = a, AC = 2a, BAC = 120 . Cạnh bên SA vuông góc 
với đáy, mặt phẳng (SBC) tạo với đáy một góc 600 .
 a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
 b) Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
 Lời giải
 Áp dụng định lí côsin trong tam giác ABC , ta có
 = 2 + 2 - · =
 S BC AB AC 2AB.AC.cos BAC a 7 .
 Gọi E là hình chiếu của A trên BC , suy ra AE ^ BC .
 ïì BC ^ AE
 Ta có íï Þ BC ^ (SAE)Þ BC ^ SE .
 îï BC ^ SA
 ü
 (SBC)Ç(ABC)= BC ï
 ï
 Do SE Ì (SBC),SE ^ BC ýï
 ï
 Ì ^ ï
 AE (ABC), AE BCþï
 · · · 0
 Þ (SBC),(ABC)= SE, AE = SEA = 60 .
 H A K
 C 1 1 · a 3
 Ta có SDABC = AE.BC = AB.AC.sin BAC nên AE = .
 2 2 7
 a) Kẻ AK ^ SE (K Î SE). (1)
 E
 Ta có BC ^ (SAE)Þ BC ^ AK . (2)
 B
 Từ (1) và (2), suy ra AK ^ (SBC) nên d(A,(SBC))= AK .
 · · 3a 3a
Trong tam giác vuông AKE , ta có AK = AE.sin KEA = AE.sinSEA = . Vậy d(A,(SBC))= AK = .
 2 7 2 7
 ïì BH ^ AC
b) Gọi H là hình chiếu của B trên AC . Ta có íï Þ BH ^ (SAC). Do đó
 îï BH ^ SA
 d(B,(SAC))= BH .
 · · a 3 · · 0 a 3
Ta có BH = AB.sin BAH = AB.sin BAC = (do BAH + BAC = 180 ). Vậy d(B,(SAC))= .
 2 2
Bài 15. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a 3 và vuông góc với đáy.
 a) Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
 b) Tính khoảng cách từ điểm C đến mặt phẳng (SBD).
 c) Tính khoảng cách từ trọng tâm của tam giác SAB đến mặt phẳng (SAC).
 Lời giải
 ïì BC ^ AB
a) Kẻ AH ^ SB (H Î SB). Ta có íï Þ BC ^ (SAB)Þ BC ^ AH . Suy ra AH ^ (SBC). Do đó 
 îï BC ^ SA
 d(A,(SBC))= AH .
 SA.AB a 3 a 3
Trong tam giác vuông SAB , ta có AH = = . Vậy d(A,(SBC))= AH = .
 SA2 + AB2 2 2 b) Gọi O = AC ÇBD . Ta có 
 S
 d(C,(SBD))= d(A,(SBD)).
 Kẻ AK ^ SO (K Î SO). (1)
 ïì BD ^ AC
 Ta có íï Þ BD ^ (SAC)Þ BD ^ AK . (2)
 îï BD ^ SA
 Từ (1) và (2), suy ra AK ^ (SBD) nên d(A,(SBD))= AK .
 G Trong tam giác vuông SAO , ta có 
 K
 A D a 2
 H a 3.
 F SA.AO a 21
 AK = = 2 = .
 E SA2 + AO2 a2 7
 3a2 +
 O 2
 a 21
 B C Vậy d(C,(SBD))= d(A,(SBD))= AK = .
 7
c) Gọi E là trung điểm AB , G là trọng tâm tam giác SAB . Ta có 
 SG 2
 d(G,(SAC))= d(E,(SAC))= d(E,(SAC)).
 SE 3
 ïì EF ^ AO
Gọi F là trung điểm AO , suy ra EF / /BO nên EF ^ AO . Ta có íï Þ EF ^ (SAC). Do đó d(E,(SAC))= EF .
 îï EF ^ SA
 BO BC a 2 2 2 a 2
Ta có EF = = = . Vậy d(G,(SAC))= d(E,(SAC))= EF = .
 2 4 4 3 3 6
Bài 16. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a ; SA = SB = SC = SD = a 2 . Tính khoảng 
cách từ điểm O đến mặt phẳng (SBC).
 Lời giải
Do O là tâm hình vuông nên OA = OB = OC = OD .
Mà SA = SB = SC = SD , suy ra SO là trục của đường tròn S
ngoại tiếp hình vuông ABCD nên SO ^ (ABCD).
 a 6
Trong tam giác vuông SOA , ta có SO = SA2 - OA2 = .
 2
 a
Gọi M là trung điểm BC , suy ra OM = và OM ^ BC .
 2
Gọi K là hình chiếu của O trên SM , suy ra OK ^ SM . (1)
 ì
 ï BC ^ OM
Ta có í Þ BC ^ (SOM)Þ BC ^ OK . (2) K
 îï BC ^ SO
 D C
Từ (1) và (2), suy ra OK ^ (SBC) nên d(O,(SBC))= OK .
Trong tam giác vuông SOM , ta có 
 O M
 SO.OM a 42
 = =
 OK . A B
 SO2 + OM2 14
 a 42
Vậy d(O,(SBC))= OK = .
 14