Tự luận Hình học Lớp 11 - Chương 2 - Chủ đề 4: Hai mặt phẳng vuông góc

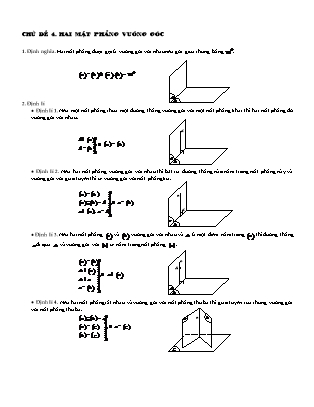
 CHUÛ ÑEÀ 4. HAI MAËT PHAÚNG VUOÂNG GOÙC
1. Định nghĩa. Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 900 .
 ·
 (a)^ (b)Û (a),(b)= 900
 a
 b
2. Định lí 
 ● Định lí 1. Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó 
 vuông góc với nhau.
 d
 ü
 d Ì (a)ï
 ýï Þ (a)^ (b)
 ^ b ï
 d ( )þï
 a
 b
 ● Định lí 2. Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và 
 vuông góc với giao tuyến thì sẽ vuông góc với mặt phẳng kia.
 ü
 (a)^ (b) ï a
 ï
 (a)Ç(b)= d ýï Þ a ^ (b)
 ï
 Ì a ^ ï d
 a ( ), a dþï
 a
 b
 ● Định lí 3. Nếu hai mặt phẳng (a) và (b) vuông góc với nhau và A là một điểm nằm trong (a) thì đường thẳng 
 a đi qua A và vuông góc với (b) sẽ nằm trong mặt phẳng (a).
 ü a
 (a)^ (b)ï
 ï A
 A Î (a) ï
 ýï Þ a Ì (a)
 A Î a ï
 ï
 a ^ (b) ï a
 þï b
 ● Định lí 4. Nếu hai mặt phẳng cắt nhau và vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc 
 với mặt phẳng thứ ba.
 ü a
 (a)Ç(b)= aï a b
 ï
 (a)^ (g) ýï Þ a ^ (g)
 ï
 b ^ g ï
 ( ) ( ) þï
 g 3. Để chứng minh hai mặt phẳng (a) và (b) vuông góc với nhau ta có thể sử dụng một trong các cách sau:
 Chứng minh trong (a) có một đường thẳng d mà d ^ (b).
 ·
 Chứng minh (a),(b)= 900 .
 VẤN ĐỀ 1. Chứng minh hai mặt phẳng vuông góc
Bài 1. Cho tam giác đều ABC cạnh a . Gọi D là điểm đối xứng với A qua BC . Trên đường thẳng vuông góc với mặt 
 a 6
phẳng (ABC) tại D lấy điểm S sao cho SD = . Chứng minh (SAB)^ (SAC).
 2
 Lời giải
 Gọi I là trung điểm của BC thì AI ^ BC và I cũng là trung 
 S điểm của AD . Ta có
 ïì BC ^ AD
 íï Þ BC ^ (SAD)Þ BC ^ SA .
 îï BC ^ SD
 Dựng IH ^ SA (H Î SA), khi đó ta có 
 ì
 ï SA ^ IH
 H í Þ SA ^ (HCB)Þ SA ^ BH . (1)
 îï SA ^ CB
 IH AI
 Ta có DAHI ∽ DADS suy ra = . Mà 
 B A SD AS
 a 3 3a 2
 AI = , AD = 2AI = a 3 , SA2 = AD2 + SD2 =
 I 2 2
 AI.SD a BC
 D C suy ra IH = = = .
 AS 2 2
 · 0
Tam giác HBC có trung tuyến IH bằng nửa cạnh đáy BC nên BHC = 90 hay BH ^ HC . (2)
Từ (1) và (2), suy ra BH ^ (SAC)Þ (SAB)^ (SAC).
Bài 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với đáy. Gọi M là trung điểm 
 AC . Chứng minh (SAB)^ (SBC) và (SBM)^ (SAC).
 Lời giải S
● Tam giác ABC vuông tại B nên BC ^ BA . (1)
Hơn nữa SA ^ (ABC)Þ SA ^ BC . (2)
Từ (1) và (2), suy ra BC ^ (SAB)Þ (SBC)^ (SAB).
● Do tam giác ABC cân tại B và M là trung điểm AC
 M
nên BM ^ AC . (3) A C
Lại có SA ^ (ABC)Þ SA ^ BM . (4)
Từ (3) và (4), suy ra BM ^ (SAC)Þ (SBM)^ (SAC).
 B Bài 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , SA vuông góc với đáy. Gọi H, K lần lượt là hình 
 chiếu của A trên SB , SC và I là giao điểm của HK với mặt phẳng (ABC). Chứng minh 
 a) (AHK)^ (SBC).
 b) AI ^ AK .
 Lời giải
 S ïì BC ^ AB
 a) Ta có íï Þ BC ^ (SAB)Þ BC ^ AH . (1)
 îï SA ^ BC
 K Theo giả thiết AH ^ SB . (2)
 Từ (1) và (2), suy ra AH ^ (SBC)Þ AH ^ SC . (*)
 Lại có theo giả thiết SC ^ AK . (* *)
 H
 Từ (*) và (* *), suy ra SC ^ (AHK)Þ (SBC)^ (AHK).
 A C
 ì
 ï SC ^ (AHK)
 b) Ta có íï Þ SC ^ AI . (3)
 ï Ì
 îï AI (AHK)
 B Vì SA ^ (ABC)Þ SA ^ AI . (4)
 Từ (3) và (4), suy ra AI ^ (SAC)Þ AI ^ AK .
 I
 Bài 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C , mặt bên SAC là tam giác đều và mằm trong mặt 
 phẳng vuông góc với đáy. Gọi I là trung điểm của SC . Chứng minh (ABI)^ (SBC).
 Lời giải S
Tam giác SAC có I là trung điểm của SC nên AI ^ SC . (1)
Gọi H là trung điểm AC suy ra SH ^ AC . Mà (SAC)^ (ABC) 
theo giao tuyến AC nên SH ^ (ABC) do đó SH ^ BC . Hơn nữa I
theo giả thiết tam giác ABC vuông tại C nên BC ^ AC . Từ đó 
suy ra BC ^ (SAC)Þ BC ^ AI . (2) A B
Từ (1) và (2), suy ra AI ^ (SBC)Þ (ABI)^ (SBC).
 H
 C
 Bài 5. Cho hình chóp S.ABC có SA vuông góc với đáy (ABC). Gọi H , K lần lượt là trực tâm của các tam giác ABC 
 và SBC . Chứng minh rằng
 a) Ba đường thẳng AH , BC và SK đồng quy.
 b) (SAB)^ (CHK) và (SBC)^ (CHK).
 c) HK ^ (SBC).
 Lời giải
 a) Gọi E = AH ÇBC . 
 ü
 SA ^ (ABC)Þ SA ^ BCï
 Ta có ý Þ BC ^ (SAE).
 ï
 AE ^ BC þï Suy ra BC ^ SE mà K là trực tâm của tam giác SBC nên S , K , E thẳng hàng.
Vậy ba đường thẳng AH , BC và SK đồng quy tại E .
 ü
 S SA ^ (ABC)Þ SA ^ CHï
 b) Ta có ý Þ CH ^ (SAB)
 ï
 CH ^ AB þï
 suy ra CH ^ SB . (1)
 Hơn nữa, do K là trực tâm tam giác SBC nên CK ^ SB . (2)
 Từ (1) và (2), suy ra SB ^ (CHK).
 Mà SB Ì (SAB) nên (SAB)^ (CHK) 
 A C
 và SB Ì (SBC) nên (SBC)^ (CHK).
 K
 c) Theo câu a, ta có BC ^ (SAE)Þ BC ^ HK . (3)
 H
 ^ Þ ^
 E Theo câu b, ta có SB (CHK) SB HK . (4)
 Từ (3) và (4), suy ra HK ^ (SBC).
 B
Bài 6. Cho tam giác ABC . Vẽ BB' và CC' cùng vuông góc với mặt phẳng (ABC). Gọi H , K lần lượt là hình chiếu 
vuông góc của A trên BC , B'C' . Chứng minh (AB'C')^ (AHK).
 Lời giải B'
 K
 ïì AH ^ BC C'
Ta có íï Þ AH ^ (BCC' B')Þ AH ^ B'C' . (1)
 îï BB' ^ AH
Theo giả thiết AK ^ B'C' . (2)
 H
 B
Từ (1) và (2), suy ra B'C' ^ (AHK)Þ (AB'C')^ (AHK). C
 A
Bài 7. Cho tứ diện SABC có SBC và ABC nằm trong hai mặt phẳng vuông góc với nhau. Tam giác SBC đều cạnh a , 
tam giác ABC vuông tại A . Gọi H , I lần lượt là trung điểm của BC và AB . Chứng minh (SHI)^ (SAB).
 Lời giải
 S
 Do SBC là tam giác đều có H là trung điểm BC nên 
 SH ^ BC . Mà (SBC)^ (ABC) theo giao tuyến BC .
 Suy ra SH ^ (ABC) nên SH ^ AB . (1)
 Hơn nữa H , I lần lượt là trung điểm của BC và AB suy ra 
 HI là đường trung bình của tam giác ABC nên HI / /AC . 
 Mà tam giác ABC vuông tại A suy ra AC ^ AB .
 B H C Do đó HI ^ AB . (2)
 Từ (1) và (2), suy ra AB ^ (SHI)Þ (SAB)^ (SHI).
 I
 A Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên (SAD) là tam giác cân tại S và nằm trong mặt 
phẳng vuông góc với đáy. Gọi M , N , P lần lượt là trung điểm của SB , BC , CD . Chứng minh (SBP)^ (AMN).
 Lời giải
 Gọi H là trung điểm AD , do tam giác SAD cân tại S nên 
 S
 SH ^ AD . Mà (SAD)^ (ABCD) theo giao tuyến AD suy ra 
 SH ^ (ABCD)Þ SH ^ BP . (1)
 Dễ thấy hai tam giác vuông CBP và DCH bằng nhau, nên ta 
 M · · · · 0
 có CBP = DCH Þ CBP + HCB = 90 Þ BP ^ CH . (2)
 Từ (1) và (2), suy ra BP ^ (SHC)Þ BP ^ SC .
 BP ^ HC ïü
 Ta có ýï Þ BP ^ AN . (*)
 A B HC / /ANþï
 H BP ^ SC ïü
 Lại có ï Þ BP ^ MN . * *
 N ý ( )
 SC / /MNþï
 D P C Từ (*) và (* *), suy ra BP ^ (AMN)Þ (SBP)^ (AMN).
Bài 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy. Gọi BE , DF là các đường cao 
của tam giác SBD . Chứng minh rằng (ACF)^ (SBC) và (AEF)^ (SAC).
 Lời giải
 S
 ì
 ï SA ^ (ABCD)Þ SA ^ AD
● Ta có í Þ AD ^ (SAB)Þ AD ^ SB . (1)
 ï
 îï AD ^ AB
Theo giả thiết, ta có DF ^ SB . (2) F
Từ (1) và (2), suy ra SB ^ (ADF)Þ SB ^ AF . (*) E
 ì
 ï SA ^ (ABCD)Þ SA ^ BC
Lại có í Þ BC ^ (SAB)Þ BC ^ AF . (* *)
 ï
 îï BC ^ AB
Từ (*) và (* *), suy ra AF ^ (SBC)Þ (ACF)^ (SBC). A B
● Theo chứng minh trên AF ^ (SBC)Þ AF ^ SC .
Chứng minh tương tự ta được AE ^ SC .
Từ đó suy ra SC ^ (AEF)Þ (SAC)^ (AEF). D C
Bài 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy. Gọi M là trung điểm BC , N là 
điểm trên cạnh CN thỏa mãn ND = 3NC . Chứng minh rằng (SAM)^ (SMN).
 Lời giải
 a 3a a
Gọi cạnh hình vuông là a . Suy ra BM = MC = ; ND = , NC = .
 2 4 4
 5a2 5a2 25a2
Ta có AM2 = AB2 + BM2 = ; MN2 = MC2 + NC2 = ; AN2 = AD2 + ND2 = .
 4 16 16
 5a2 5a2 25a2
Xét tam giác AMN , ta có AM2 + MN2 = + = = AN2 .
 4 16 16 S Suy ra tam giác AMN vuông tại N nên NM ^ AM . (1)
 Hơn nữa do SA ^ (ABCD)Þ SA ^ NM . (2)
 Từ (1) và (2), suy ra NM ^ (SAM)Þ (SMN)^ (SAM).
 A B
 M
 D N C
Bài 11. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a , AD = a 2 ; cạnh bên SA vuông góc với 
đáy. Gọi M là trung điểm của AD , I là giao điểm của AC với BM . Chứng minh (SAC)^ (SMB).
 Lời giải S
Ta có SA ^ (ABCD)Þ SA ^ BM . (1)
 · AB
Xét tam giác vuông ABM , ta có tan AMB = = 2 .
 AM
 · AD
Xét tam giác vuông ADC , ta có cotCAD = = 2 .
 CD
Xét tam giác AIM , ta có 
 · · · · A M
 tan AMI = tan AMB = 2 = cotCAD = cot IAM . D
Do đó tam giác AIM vuông tại I nên BM ^ AC . (2) I
Từ (1) và (2), suy ra BM ^ (SAC)Þ (SBM)^ (SAC). B C
Bài 12. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Các tam giác SAC và SBD cân tại S . Gọi O là tâm hình 
thoi. Chứng minh SO ^ (ABCD) và (SAC)^ (SBD).
 Lời giải
 S
 ● Tam giác SAC cân tại S có trung tuyến SO nên SO ^ AC .
 Tam giác SBD cân tại S có trung tuyến SO nên SO ^ BD .
 ïì SO ^ AC
 Ta có íï Þ SO ^ (ABCD).
 îï SO ^ BD
 ● Theo trên ta có SO ^ AC . (1)
 Mặt khác AC ^ BD (do ABCD là hình thoi). (2)
 A D
 Từ (1) và (2), suy ra AC ^ (SBD)Þ (SAC)^ (SBD).
 O
 B C 2a 3
Bài 13. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh a , BD ; SO vuông góc với đáy và 
 3
 SB = a . Chứng minh SAB  SAD .
 Lời giải
 Gọi K là trung điểm cạnh SA .
 S
 Do SB AB a suy ra BK  SA . 1 
 Ta có SO2 = SB2 - BO2 = AB2 - BO2 = AO2 .
 AC
 Suy ra SO = AO = nên tam giác SAC vuông tại S (do 
 2
 K trung tuyến SO bằng nửa cạnh đáy AC ).
 Áp dụng hệ thức lượng trong tam giác vuông SAC , ta có 
 4a2
 SA2 = AO.AC = 2AO2 = 2(AB2 - BO2 )= .
 3
 A D 2a 3
 Suy ra SA = = BD .
 3
 O Tam giác SOA vuông tại O có trung tuyến OK nên 
 SA BD
 C OK = = . Suy ra DBKD vuông tại K (do trung tuyến 
 B 2 2
 OK bằng nửa cạnh đáy BD ) hay BK ^ DK . 2 
Từ 1 và 2 , suy ra BK  SAD SAB  SAD .
Bài 14. Cho hình lập phương ABCD.A' B'C' D' . Chứng minh rằng (AB'C' D)^ (BCD' A') và AC' ^ (CB' D').
 Lời giải
 ^
● Vì ABB' A' là hình vuông suy ra BA' AB' . (1) A D
 AD ^ AB ïü
Mặt khác ýï Þ AD ^ (ABB' A')Þ AD ^ BA' . (2)
 AD ^ AA'þï B C
Từ 1 và 2 , suy ra 
 BA'  AB'C' D BCD' A'  AB'C' D .
● Giả sử cạnh hình lập phương là a .
Ta có AC = AB' = AD' = a 2 vì là các đường chéo của hình 
 A' D'
vuông. (3)
Lại có C'C = C' B' = C' D' = a . (4)
 B' C'
Từ 3 và 4 , suy ra AC' là trục của đường tròn ngoại tiếp 
tam giác (CB' D') nên AC' ^ (CB' D').
Bài 15. Cho hình hộp chữ nhật ABCD.A' B'C' D' . Gọi K là hình chiếu của C trên BD , H là hình chiếu của C trên 
 C'K . Chứng minh (CDH)^ (C' BD).
 Lời giải D' C'
 Do ABCD.A' B'C' D' là hình hộp chữ nhật nên BD ^ CC' . 
 Theo giả thiết CK ^ BD . 
 A' B'
 H Từ đó suy ra BD ^ (CKC')Þ BD ^ CH . (*)
 Hơn nữa từ giả thiết ta lại có CH ^ C'K . (* *)
 D
 C Từ * và * * , suy ra CH ^ (C' BD).
 Ì ^
 K Mà CH (CDH) nên (CDH) (C' BD).
 A B
 · 0
Bài 16. Cho lăng trụ đứng ABC.A' B'C' có AB = a, AC = 2a, BAC = 120 và AA' = 2a 5 . Gọi M là trung điểm của 
 uuur 1 uuur
cạnh CC' và N là điểm thỏa mãn AN = - AC .
 4
a) Chứng minh rằng (A' MB')^ (BMN).
 a 3
b) Trên đoạn BM lấy điểm E sao cho BE = . Chứng minh rằng A' B ^ NE .
 8
 Lời giải
 2 2 2 · A'
a) Ta có BC = AB + AC - 2AB.AC cos BAC = a 7 ; C'
 A' M = A'C'2 + C' M2 = 3a ; BM = BC2 + CM2 = 2a 3 .
 2 = 2 + 2 = 2 = 2 + 2
Suy ra A' B A' A AB 21a A' M BM . B'
Do đó tam giác A' MB vuông tại M , suy ra A' M ^ MB . (1)
 uuur uuur
 1 a M
Theo đề AN = - AC nên AN = . Suy ra
 4 2
 81a2 45a2
 A' N2 = AA'2 + AN2 = ; MN2 = MC2 + CN2 = .
 4 4
 2 2
 2 2 2 45a 81a 2
Suy ra MN + A' M = 9a + = = A' N . N A
 4 4 C
Do đó tam giác A' NM vuông tại M , suy ra A' M ^ MN . (2)
 E
Từ (1) và (2), suy ra A' M ^ (BMN)Þ (A' MB')^ (BMN).
 r uuur r uuur r B
b) Đặt AA' = a, AB = b, AC = c .
 a 3 1
Vì BM = 2a 3 và BE = suy ra BE = BM . Ta có
 8 16
 uuur uuur uuur uuur uuur 1 uuuur r r 1 r 1 r r r
 ● BM = BC + CM = AC - AB+ AA' = c - b + a = a- b + c .
 2 2 2
 uuur uuur uuur uur 1 uuur uuur 1 uuur 1 r 15 r 5 r
 ● NE = NA + AB+ BE = AC + AB+ BM = a + b + c .
 4 16 32 16 16
 uuur uuur æ r r röæ r r rö r 2 r 2 r 2 r r
 ç 1 15 5 ÷ç1 ÷ 1 15 5 5
Suy ra NE.BM = ç a + b + c÷ç a- b + c÷= a - b + c + b.c = 0 .
 èç32 16 16 ø÷èç2 ø÷ 64 16 16 8
Do đó NE ^ BM . (3)
Mặt khác theo chứng minh trên A' M ^ (BMN)Þ A' M ^ NE . (4)
Từ (3) và (4), suy ra NE ^ (A' BM)Þ NE ^ A' B . · 0
Bài 17. Cho lăng trụ đứng ABC.A' B'C' có AB = a, AC = 2a, BAC = 120 và AA' = a 3 . Gọi M là trung điểm cạnh 
bên BB' . Chứng minh rằng (MAC)^ (MA'C').
 Lời giải
 Gọi H là hình chiếu của B lên AC .
 A' C' · 0 a a 3
 Ta có AH = AB.cos BAH = a.cos60 = và HB = .
 2 2
 Tam giác A' AH vuông tại A nên 
 13a2
 B' A' H2 = A' A2 + AH2 = .
 4
 Trong tam giác A' MB' , ta có
 3a2 7a2
 A' M2 = A' B'2 + B' M2 = a2 + = .
 4 4
 Trong tam giác MHB , ta có
 M 3a2 3a2 3a2
 MH2 = MB2 + BH2 = + = .
 4 4 2
 7a2 3a2 13a2
 H C Suy ra MH2 + A' M2 = + = = A' H2 .
 A 4 2 4
 Do đó tam giác A' MH vuông tại M hay A' M ^ MH . (1)
 Áp dụng định lí hàm số Côsin cho tam giác A' B'C' , ta có
 B 2 2 ·
 BC = AB + AC - 2AB.AC.cos BAC = a 7 .
 2 2 æ ö2 2
 2 2 2 2 3a 31a 2 2 2 2 ç a÷ 37a
Suy ra C' M = B'C' + B' M = 7a + = ; C' H = C'C + CH = 3a + ç2a + ÷ = nên
 4 4 èç 2ø÷ 4
 31a2 3a2 37a2
 C' M2 + MH2 = + = = C' H2 .
 4 2 4
Do đó tam giác C' MH vuông tại M hay HM ^ C' M . (2)
Từ (1) và (2), suy ra HM ^ (MA'C')Þ (MAC)^ (MA'C') .
 VẤN ĐỀ 2. Tìm thiết diện chứa một đường cho trước 
 và vuông góc với một mặt phẳng cho trước
 a 3
Bài 18. Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a , các cạnh bên đều bằng . Mặt phẳng (a) qua 
 2
 A , song song với BC và vuông góc với mặt phẳng (SBC). Xác định thiết diện tạo bởi (a) với hình chóp S.ABC .
 Lời giải
Gọi O là tâm của tam giác ABC . Do SA = SB = SC suy ra hình chiếu của S trên mặt phẳng (ABC) chính là điểm O .
Gọi I là trung điểm BC . Tam giác ABC đều nên AI ^ BC và tam giác SBC đều nên SI ^ BC .
 AI ^ BCïü
Ta có ýï Þ BC ^ (SAI)Þ (SBC)^ (SAI).
 SI ^ BC þï
Trong mặt phẳng (SAI) kẻ AH ^ SI (H Î SI) mà (SBC)^ (SAI) theo giao tuyến SI nên AH ^ (SBC). S Trong mặt phẳng (SBC), qua H kẻ đường song song với 
 BC , cắt SC ở M , cắt SB ở N thì mặt phẳng tạo bởi AH và 
 MN chính là mặt phẳng (a). Thật vậy
 ● (a) đi qua A .
 M ü
 AH Ì (a) ï
 ● ýï Þ (a)^ (SBC).
 H ^ ï
 AH (SBC)þï
 N ü
 MN Ì (a)ï
 ● ý Þ (a)/ /BC .
 ï
 A B MN / /BCþï
 Vậy thiết diện cần tìm là tam giác AMN .
 O Dễ thấy H là trung điểm của MN mà AH ^ (SBC) suy ra 
 I
 AH ^ MN . Tam giác AMN có đường cao AH vừa là trung 
 tuyến nên nó là tam giác cân đỉnh A .
 C
Bài 19. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và AB = a ; SA = a 3 và vuông góc với đáy. 
Gọi E và F lần lượt là trung điểm của SC và SB , M là điểm trên đoạn AB . Đặt AM = x (0 £ x £ a). Mặt phẳng 
 (a) chứa EM và vuông góc với (SAB).
 a) Xác định thiết diện tạo bởi (a) với hình chóp S.ABC .
 b) Tính diện tích của thiết diện theo a và x .
 Lời giải
a) Dễ chứng minh BC ^ (SAB) , suy ra (a)/ /BC .
 S
Mà BC Ì (SBC) nên (a)Ç(SBC)= d thì d / /BC .
Vậy (a) cắt mặt bên (SBC) theo giao tuyến EF .
Lí luận tương tự, để có giao tuyến MN của (a) với (ABC) 
song song với BC . E
Tứ giác EFMN là hình thang. 
 ì ïì
 ï MN / /EF / /BC ï MN ^ (SAB) ïì EF ^ FM
Dễ thấy í Þ íï suy ra íï .
 ï BC ^ SAB ï ^ ï MN ^ FM F
 îï ( ) îï EF (SAB) îï
Vậy EFMN là hình thang vuông tại M và F .
 A N C
 · SA · 0
b) Ta có tanSBA = = 3 suy ra SBA = 60 .
 AB
Tam giác SBA vuông tại S nên SB = SA2 + AB2 = 2a .
 SB M
Xét tam giác MBF , ta có BF = = a, BM = AB- AM = a- x ,
 2 B
 2 2 · 2 2
do đó FM = BF + BM - 2BF.BM.cos FBM = x - ax + a .
Tam giác ABC vuông cân tại B nên tam giác AMN cũng vuông cân tại M , suy ra MN = AM = x . Khi đó 
 æ ö
 1 1 ça ÷ 2 2
 SEFMN = (FE+ MN).FM = ç + x÷ x - ax + a .
 2 2 èç2 ø÷