Tự luận Hình học Lớp 11 - Chương 1 - Chủ đề 6: Bài tập tổng hợp

 CHUÛ ÑEÀ 6. BAØI TAÄP TOÅNG HÔÏP
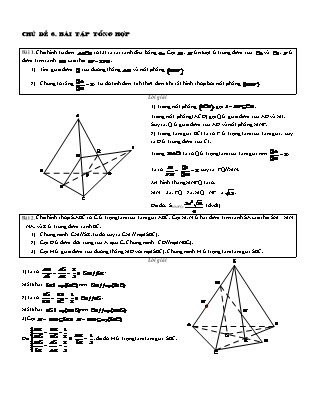
Bài 1. Cho hình tứ diện ABCD có tất cả các cạnh đều bằng 6a . Gọi M , N lần lượt là trung điểm của CA và CB ; P là 
điểm trên cạnh BD sao cho BP = 2PD .
 1) Tìm giao điểm Q của đường thẳng AD và mặt phẳng (MNP). 
 QA
 2) Chứng tỏ rằng = 2 . Từ đó tính diện tích thiết diện khi cắt hình chóp bởi mặt phẳng (MNP).
 QD
 Lời giải
 1) Trong mặt phẳng (BCD), gọi I = NP ÇCD .
 A Trong mặt phẳng (ACD) gọi Q là giao điểm của AD và MI. 
 Suy ra: Q là giao điểm của AD và mặt phẳng MNP.
 2) Trong tam giác BCI ta có P là trọng tâm của tam giác, suy 
 ra D là trung điểm của CI.
 I
 Q QA
 Trong DACI ta có Q là trọng tâm của tam giác nên = 2 .
 M QD
 PI QI
 B Ta có = = 2 suy ra PQ//MN. 
 P D PN QM
 Xét hình thang MNPQ ta có: 
 N
 MN = 3a , PQ = 2a, MQ = NP = a 13 . 
 C
 5a2 51
 Do đó: SMNPQ= (đvdt)
 4
Bài 2. Cho hình chóp S.ABC có G là trọng tâm của tam giác ABC. Gọi M, N là hai điểm trên cạnh SA sao cho SM = MN 
= NA, và K là trung điểm cạnh BC.
 1) Chứng minh GM//SK. Từ đó suy ra GM // mp(SBC).
 2) Gọi D là điểm đối xứng của A qua G. Chứng minh CD//mp(NBG).
 3) Gọi H là giao điểm của đường thẳng MD với mp(SBC). Chứng minh H là trọng tâm tam giác SBC.
 Lời giải S
 AM AG 2
1) Ta có = = Þ GM / /SK .
 AS AK 3
Mặt khác SK Ì mp(SBC) nên GM / /mp(SBC) . M
 KG KB 1
2) Ta có = = Þ CD / /BG .
 KD KC 2 N
Mặt khác BG Ì mp(NBG) nên CD / /mp(NBG) . H
3) Gọi H = DM ÇSK Þ H = DM Çmp(SBC)
 A B
 ïì HK DK 1
 ï = =
 ï HK 1
Do íï MG DG 2 Þ = , do đó H là trọng tâm tam giác SBC. G
 ï MG AG 2 SK 3 K D
 ï = =
 îï SK AK 3
 C Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của SA và CD.
 1) Tìm giao điểm E và giao điểm F của mặt phẳng (BMN) lần lượt với các đường thẳng AD và SD. Chứng minh 
 FS = 2FD.
 2) Gọi I là trung điểm ME ; AN cắt BD tại G. Chứng minh FG//(SAB) và (CDI)//(SAB).
 3) Gọi H là giao điểm của MN và SG. Chứng minh OH //GF. 
 Lời giải
 S
 M
 F
 I
 H
 A D E
 O G
 N
 B C
 ü
 Trong(ABCD) :BN Ç AD = {E}ï
1) ý Þ E = (BMN)Ç AD .
 ï
 BN Ì (BMN)þï
 ü
 Trong(SAD) :MEÇSD = {F} ï
 ý Þ F = (BMN)ÇSD .
 ï
 ME Ì (BMN)þï
 BC NC
Do BC / /DE Þ = = 1 Þ DE = BC = AD .
 DE ND
Xét tam giác SAE, ta có SD và EM là 2 đường trung tuyến cắt nhau tại F nên F là trọng tâm tam giác SAE.
2) AN cắt BD tại G G là trọng tâm tam giác ACD.
DI là đường trung bình tam giác AME nên DI//AM.
 ïì DI / /AM;CD / /AB
 ï
 ï DI,CD Ì (CDI)
Do íï Þ (SAB) / /(CDI) .
 ï AM, AB Ì (SAB)
 ï
 îï CD ÇDI = {D}
3) B,H,F là ba điểm chung của hai mặt phẳng (MBE) và (SBD) nên thẳng hàng.
 HF HG GF DG 1
Do FG / /SB Þ = = = = .
 HB HS SB DB 3
 OG OG 1 OG HF
Mà = = Þ = Þ OH / /FG .
 OB OD 3 OB HB Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, 
AD và SB.
 1) Chứng minh rằng: BD//(MNP).
 2) Tìm giao điểm của mặt phẳng (MNP) với BC.
 3) Tìm giao tuyến của hai mặt phẳng (MNP) và (SBD).
 4) Tìm thiết diện của hình chóp với mặt phẳng (MNP).
 Lời giải
 1) Do BD//MN (t/c đường trung bình).
 S
 Mà MNÌ (MNP) nên BD//(MNP).
 Q 2) Gọi I = MN ÇBC .
 ïì I Î BC
 Ta có: ï Þ I Î MNP ÇBC .
 R í ( )
 îï I Î MN
 P 3) Vì P Î (MNP)Ç(SBD) và MN//BD nên (MNP) Ç(SBD) là 
 đường thẳng d qua P và song song với BD.
 D C
 4) Gọi R = SD Çd . Nối IP cắt SC tại Q, nối RQ.
 N
 Ta có: (MNP)Ç(ABCD)= MN
 O
 (MNP)Ç(SAB)= MP
 A M B
 (MNP)Ç(SBC)= PQ
 I (MNP)Ç(SCD)= QR
 (MNP)Ç(SDA)= RN
Vậy thiết diện của hình chóp S.ABCD với mp(MNP) là ngũ giác MPQRN.