Tự luận Hình học Lớp 11 - Chương 1 - Chủ đề 5: Tính tỷ số giữa hai đoạn thẳng

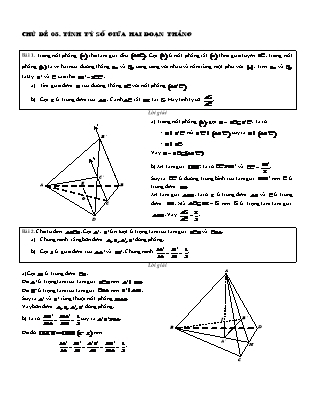
 CHUÛ ÑEÀ 05. TÍNH TYÛ SOÁ GIÖÕA HAI ÑOAÏN THAÚNG
Bài 1. Trong mặt phẳng (a) cho tam giác đều (ABC). Gọi (b) là mặt phẳng cắt (a) theo giao tuyến BC . Trong mặt 
phẳng (b) ta vẽ hai nửa đường thẳng Bx và Cy song song với nhau và nằm cùng một phía với (a). Trên Bx và Cy 
ta lấy B' và C' sao cho BB' = 2CC' .
 a) Tìm giao điểm D của đường thẳng BC với mặt phẳng (AB'C')
 AG
 b) Gọi E là trung điểm của AB . Cạnh AC cắt DE tại G . Hãy tính tỷ số .
 AC
 Lời giải
 a) Trong mặt phẳng (b), gọi D = BC ÇB'C' . Ta có 
 x
 Î Ì Ì
 B' ▪ D B'C' mà B'C' (AB'C') suy ra D (AB'C').
 ▪ D Î BC .
 Vậy D = BC Ç(AB'C').
 y
 BB'
 b) Xét tam giác DBB' , ta có CC'PBB' và CC' = .
 2
 C' Suy ra CC' là đường trung bình của tam giác DBB' nên C là 
 A E B
 trung điểm DB .
 Xét tam giác ABD , ta có E là trung điểm AB và C là trung 
 G
 C điểm DB . Mà AC ÇDE = G nên G là trọng tâm tam giác 
 AG 2
 ABD . Vậy = .
 D AC 3
Bài 2. Cho tứ diện ABCD . Gọi A' , B' lần lượt là trọng tâm của tam giác BCD và CDA . 
 a) Chứng minh rằng bốn điểm A, B, A', B' đồng phẳng.
 IA' IB' 1
 b) Gọi I là giao điểm của AA' và BB' . Chứng minh = = .
 IA IB 3
 Lời giải
 A
a) Gọi M là trung điểm CD .
Do A' là trọng tâm của tam giác BCD nên A' Î BM .
Do B' là trọng tâm của tam giác CDA nên B' Î AM .
Suy ra A' và B' cùng thuộc mặt phẳng MAB .
Vậy bốn điểm A, B, A', B' đồng phẳng.
 MB' MA' 1
b) Ta có = = suy ra A' B'PBA . I B'
 MA MB 3
 B D
Do đó DIA' B' ∽ DIAB (g - g) nên 
 A'
 IA' IB' A' B' MB' 1
 = = = = . M
 IA IB AB MA 3
 C Bài 3. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của các cạnh AB , CD và G là trung điểm của đoạn MN 
(điểm G được gọi là trọng tâm tứ diện ABCD ).
 a) Tìm giao điểm A' của đường thẳng AG với mặt phẳng (BCD).
 b) Chứng minh GA = 3GA' .
 Lời giải
 A a) Trong mặt phẳng ABN , gọi A' = AG ÇBN .
 ▪ A' Î BN mà BN Ì (BCD) suy ra A' Î (BCD).
 ▪ A' Î AG .
 M
 Vậy A' = AG Ç(BCD).
 b) Trong mặt phẳng ABN , kẻ MM 'PAA' với M ' Î BN .
 G
 Suy ra MM ' là đường trung bình của tam giác ABA' .
 B D
 Mặt khác GA' là đường trung bình của tam giác MM ' N .
 M'
 A' 1 1 1
 N Ta có GA' = MM ' mà MM ' = AA' nên GA' = AA' .
 2 2 4
 C Từ đó suy ra GA = 3GA' .
Bài 4. Cho tứ diện ABCD . Gọi I và J lần lượt là trung điểm của AC và BC . Trên cạnh BD , ta lấy điểm K sao cho 
 BK = 2KD .
 a) Tìm giao điểm E của đường thẳng CD với mặt phẳng (IJK). Chứng minh rằng DE = DC .
 b) Tìm giao điểm F của đường thẳng AD với mặt phẳng (IJK). Chứng minh rằng FA = 2FD .
 Lời giải
a) Trong mặt phẳng BCD , gọi E = CD Ç JK .
 ▪ E Î JK mà JK Ì (IJK) suy ra E Î (IJK). A
 ▪ E Î CD .
Vậy E = CD Ç(IJK).
Trong mặt phẳng (BCD), kẻ DM PBC với M Î JE .
 I
Ta có DKDM ∽ DKBJ (g - g), suy ra
 F
 DM KD 1 DM 1
 = = mà BJ = CJ nên = . N
 BJ KB 2 CJ 2
Do đó DM là đường trung bình của tam giác ECJ . C D E
 =
Vậy DE DC . M
b) Trong mặt phẳng ACD , gọi F = AD ÇIE . K
 J
 ▪ F Î IE mà IE Ì (IJK) suy ra F Î (IJK).
 ▪ F Î AD . B
Vậy F = AD Ç(IJK). Trong mặt phẳng (ACD), kẻ DN PAB với N Î IE .
 DN 1 DN 1
Suy ra DN là đường trung bình của tam giác ECI nên = mà CI = AI nên = .
 CI 2 AI 2
 FD DN 1
Ta có DFDN ∽ DFAI (g - g), suy ra = = . Vậy FA = 2FD .
 FA AI 2
Bài 5. Cho tứ diện ABCD . Gọi I , J lần lượt là trung điểm của AB và CD ; M là điểm tùy ý trên đoạn AD ( M 
không trùng các đầu mút).
 a) Xác định giao điểm N của đường thẳng BC với mặt phẳng (MIJ).
 b) Gọi K là giao điểm của MN và IJ . Chứng minh KM = KN .
 Lời giải
 a) ● Trường hợp 1. Nếu M không là trung điểm của AD .
 A Trong mặt phẳng (ABC), gọi G = MI ÇBD .
 Trong mặt phẳng (BCD), gọi N = GJ ÇBC . Ta có
 M
 ▪ N Î GJ mà GJ Ì (MIJ) suy ra N Î (MIJ).
 ▪ N Î BC .
 I
 Vậy N = BC Ç(MIJ).
 F
 K ● Trường hợp 2. Nếu M là trung điểm của AD thì MI PBD . 
 Do vậy (MIJ) cắt (BCD) theo giao tuyến song song với BD . 
 Giao tuyến này đi qua trung điểm J của CD nên nó cắt BC 
 G B E D
 tại N thì N phải là trung điểm của BC .
 N
 J b) Gọi E là trung điểm của BD và F là trung điểm của AC .
 Ta có IEPFJ PAD suy ra bốn điểm I, F, J, E cùng nằm trong 
 C
 mặt phẳng (IFJE) và ta có AD P(IFJE).
Do vậy, qua AD ta có thể dựng được một mặt phẳng (b)P(IFJE). Tương tự ta chứng minh được BC P(IFJE) và qua 
 BC ta có thể dựng được mặt phẳng (g)P(IFJE).
Ba mặt phẳng song song (b)P(IFJE)P(g) định ra trên hai cát tuyến AB và MN những đoạn thẳng tương ứng tỉ lệ nên
 KM IA
 = = 1 hay KM = KN .
 KN IB
Bài 6. Cho tứ diện ABCD . Gọi I , M lần lượt là trung điểm của AB và BC ; G là trọng tâm tam giác ACD . 
 a) Xác định giao điểm P của đường thẳng CD với mặt phẳng (IGM).
 PC
 b) Tính tỷ số .
 PD
 Lời giải a) Gọi J là trung điểm CD . Trong mặt phẳng (ABJ), gọi E = GI ÇBJ .
Trong mặt phẳng (BCD), gọi P = EM ÇCD . Ta có
 ▪ P Î EM mà EM Ì (IGM) suy ra E Î (IGM).
 ▪ P Î CD .
Vậy P = CD Ç(IGM).
 b) Gọi K là trung điểm BJ , suy ra IK là đường trung 
 A
 bình của tam giác ABJ nên IK PAJ .
 Do IK PAJ nên IK PGJ .
 Xét tam giác EIK , ta có
 EJ JG JG JG 1 2 I
 = = = 2. = 2. = .
 EK KI JA JA 3 3
 2
 Suy ra 3EJ = 2EK Û 3EJ = 2(EJ + JK) G
 D B
 Û EJ = 2JK = JB
 K
 hay J là trung điểm của EB .
 Trong tam giác BCE , ta có CJ và EM là các đường 
 J M
 trung tuyến giao nhau tại P nên P là trọng tâm. Do P
 đó PC = 2PJ (1)
 E C
 Û 3PC = 2(PJ + PC)= 2CJ = 2DJ . (2)
 PC 1
Cộng (1) và (2) vế theo vế ta được 4PC = 2(PJ + DJ)= 2DP . Vậy = .
 PD 2
Bài 7. Cho hình chóp S.ABC có G là trọng tâm của tam giác ABC . Gọi M là điểm trên cạnh SA sao cho MA = 2MS ; 
 K là trung điểm cạnh BC và D là điểm đối xứng của A qua G . Xác định giao điểm H của đường thẳng SK với mặt 
 HK
phẳng (MCD) và tính tỷ số .
 SK
 Lời giải
 Trong mặt phẳng (SAD), gọi H = MD ÇSK . Ta có
 S
 ▪ H Î MD mà MD Ì (MCD) suy ra H Î (MCD).
 ▪ H Î SK .
 M
 Vậy H = SK Ç(MCD).
 MS GK 1
 Ta có = = suy ra MG PSK .
 MA GA 2
 H
 HK DK 1
 Trong tam giác DMG , ta có = = . (1)
 A B MG DG 2
 MG AG 2
 G Trong tam giác SAK , ta có = = . (2)
 K D SK AK 3
 HK 1
 Từ (1) và (2), suy ra = .
 C SK 3 Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của AB và SC .
 a) Xác định giao điểm I của đường thẳng AN và (SBD); giao điểm J của MN và (SBD).
 b) Chứng minh IA = 2IN và JM = JN .
 IJ
 c) Chứng minh I , J , B thẳng hàng và tính tỷ số .
 IB
 Lời giải
 a) Xác định giao điểm I .
 ● Chọn mặt phẳng phụ (SAC)É AN .
 S
 ● Gọi O = AC ÇBD . Ta có (SAC)Ç(SBD)= SO .
 ● Trong mặt phẳng (SAC), gọi I = AN ÇSO . Ta có
 ▪ I Î SO mà SO Ì (SBD) suy ra I Î (SBD).
 N ▪ I Î AN .
 Vậy I = AN Ç(SBD) .
 I Xác định giao điểm J .
 J ● Chọn mặt phẳng phụ (SMC)É MN .
 D C
 ● Gọi E = MC ÇBD . Ta có (SMC)Ç(SBD)= SE .
 P F
 O ● Trong mặt phẳng (SMC), gọi J = MN ÇSE . Ta có
 E
 ▪ J Î SE mà SE Ì SBD suy ra J Î SBD .
 A M B ( ) ( )
 ▪ J Î MN .
 Vậy J = MN Ç(SBD).
b) Trong tam giác SAC , ta có SO và AN là các đường trung tuyến nên I là trọng tâm. Vậy IA = 2IN .
 ME MB 1
Ta có DEMB ∽ DECD (g - g), suy ra = = nên CE = 2ME .
 CE CD 2
Gọi F là trung điểm EC , ta có ME = EF = FC và NF PSE suy ra NF PJE .
 ïì NF PJE
Xét tam giác MNF , ta có íï suy ra J là trung điểm MN . Vậy JM = JN .
 îï ME = EF
 ì ì
 ïì I Î AN ï AN Ì (ANB) ï I Î (ANB)
c) Ta có íï mà íï suy ra íï hay I là điểm chung của hai mặt phẳng (ANB) và (SBD).
 ï I Î SO ï Ì ï Î
 îï îï SO (SBD) îï I (SBD)
 ì ì
 ïì J Î MN ï MN Ì (ANB) ï J Î (ANB)
 íï mà íï suy ra íï hay J là điểm chung của hai mặt phẳng (ANB) và (SBD).
 ï J Î SE ï Ì ï Î
 îï îï SE (SBD) îï J (SBD)
 ì ì
 ïì B Î AB ï AB Ì (ANB) ï B Î (ANB)
 íï mà íï suy ra íï hay B là điểm chung của hai mặt phẳng (ANB) và (SBD).
 ï B Î SB ï Ì ï Î
 îï îï SB (SBD) îï B (SBD)
Vậy ba điểm I , J , B cùng thuộc hai mặt phẳng (ANB) và (SBD) nên thẳng hàng. Trong mặt phẳng (ANB), kẻ MP PIB với P Î AN . Ta có
 IJ NJ 1 PM AM 1
 = = và = = .
 PM NM 2 IB AB 2
 IJ 1
Từ đó suy ra = .
 IB 4
Bài 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của SA và CD .
 a) Tìm giao điểm E và giao điểm F của mặt phẳng (BMN) lần lượt với các đường thẳng AD và SD .
 b) Chứng minh FS = 2FD .
 Lời giải
a) Trong mặt phẳng (ABCD), gọi E = BN Ç AD . Ta có
 ▪ E Î BN mà BN Ì (BMN) suy ra E Î (BMN).
 ▪ E Î AD . S
Vậy E = AD Ç(BMN).
Trong mặt phẳng (SAD), gọi F = MEÇSD .
 M
Ta có
 F
 ▪ F Î ME mà ME Ì (BMN) 
 suy ra F Î (BMN).
 A D E
 ▪ F Î SD .
Vậy F = SD Ç(BMN). N
 B C
 ïì DN PAB
 ï
b) Xét tam giác EAB , ta có í 1
 ï DN = AB
 îï 2
suy ra DN là đường trung bình nên D là trung điểm AE .
Xét tam giác SAE , ta có SD và ME là các đường trung tuyến nên F là trọng tâm. Vậy FS = 2FD .
Bài 10. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SC ; O là giao điểm của hai 
đường chéo AC và BD ; N là trung điểm của OB .
 a) Xác định giao điểm I của đường thẳng SD và mặt phẳng (AMN).
 SI
 b) Tính tỷ số .
 ID
 Lời giải
a) Trong mặt phẳng (SAC), gọi K = AM ÇSO .
Trong mặt phẳng (SBD), gọi I = NK ÇSD . Ta có
 ▪ I Î NK mà NK Ì (AMN) suy ra I Î (AMN).
 ▪ I Î SD .
Vậy I = SD Ç(AMN). b) Trong tam giác SAC , ta có SO và AM là các đường trung S
tuyến nên K là trọng tâm.
Trong mặt phẳng (SBD), kẻ OP PNI với P Î SD . Ta có 
 DI DN
 = = 3 suy ra DI = 3PI . I
 PI ON
 M
 SI SK K
Trong tam giác SOP , ta có = = 2 suy ra SI = 2PI . P
 PI OK
 SI 2PI 2 B A
Vậy = = .
 ID 3PI 3 N
 O
 C D
Bài 11. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M và N là trung điểm của SA và SC . Tìm giao điểm 
 SK
 K của đường thẳng SD và mặt phẳng (BMN) và tính tỷ số .
 SD
 Lời giải
 = Ç
 S Trong mặt phẳng (ABCD), gọi O AC BD .
 Trong mặt phẳng (SAC), gọi E = MN ÇSO .
 Trong mặt phẳng (SBD), gọi K = BEÇSD . Ta có
 K
 N ▪ K Î BE mà BE Ì (BMN) suy ra K Î (BMN).
 E
 M ▪ K Î SD .
 Vậy K = SD Ç(BMN).
 I
 Trong mặt phẳng (SAC), kẻ OI PBK với I Î SD .
 B C
 ì
 ï OI PBK
 O Xét tam giác DBK , ta có í suy ra OI là đường 
 îï OB = OD
 A D trung bình nên I là trung điểm KD . (1)
 SK SE SM 1
Xét tam giác SOI , ta có EK POI nên = = = . Do đó K là trung điểm SI . (2)
 SI SO SA 2
 SK 1
Từ (1) và (2), suy ra = .
 SD 3
Bài 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. E , F lần lượt là trọng tâm các tam giác SAD , SCD .
 a) Xác định giao điểm I của đường thẳng SB và mặt phẳng (DEF).
 SI
 b) Tính tỷ số .
 SB
 Lời giải a) Gọi M , N lần lượt là trung điểm của AD và CD . S
 SE SF 2
Ta có = = suy ra EF PMN .
 SM SN 3
Trong mặt phẳng (ABCD), gọi H = MN ÇBD .
 I
Trong mặt phẳng (SMN) , gọi L = EF ÇSH .
Trong mặt phẳng (SBD), gọi I = DL ÇSB . Ta có K F
 L
 E
 ▪ I Î DL mà DL Ì (DEF) suy ra I Î (DEF).
 ▪ I Î SB . D N C
 = Ç
Vậy I SB (DEF). M H
 O
b) Trong tam giác SBD , kẻ HK PDI với K Î SB .
 B
 SI SL SE SI A
Xét tam giác SHK , ta có = = = 2 suy ra IK = .
 IK LH EM 2
Trong mặt phẳng (ABCD), gọi O = AC ÇBD suy ra O là trung điểm BD .
 DH DM DN 1 BH
Xét tam giác ACD , ta có = = = suy ra H là trung điểm OD . Do đó = 3 .
 DO DA DC 2 HD
 BK BH 3
Xét tam giác BDI , ta có = = 3 suy ra BK = 3KI = SI .
 KI HD 2
 SI SI SI 1
Vậy = = = .
 SB SI + IK + KB 1 3 3
 SI + SI + SI
 2 2
Bài 13. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của cạnh SC . Mặt phẳng (a) qua 
 AM và song song với BD .
 a) Tìm E , F lần lượt là giao điểm của (a) với SB và SD .
 S S
 b) Tính tỉ số của DSME và DSMF .
 SDSBC SDSCD
 c) Gọi K là giao điểm của ME và CB , J là giao điểm của MF và CD . Chứng minh ba điểm K , A , J nằm trên 
 EF
 một đường thẳng song song với EF và tính tỷ số .
 KJ
 Lời giải
a) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC ÇBD .
Trong mặt phẳng SAC , gọi I = SO Ç AM . Chọn mặt phẳng phụ (SBD) chứa SB và SD .
 ì
 ï I Î (a)Ç(SBD)
 ï
Ta có íï BD Ì (SBD) suy ra giao tuyến của hai mặt phẳng (SBD) và (a) là đường thẳng qua I và song song với BD .
 ï
 ï P a
 îï BD ( )
Giao tuyến này cắt SB tại E , cắt SD tại F . S
 M
 F
 I
 E
 D C
 J
 O
 A B
 K
 SE SF SI 2
b) Trong tam giác SAC , ta có SO và AM là hai đường trung tuyến nên I là trọng tâm. Suy ra = = = .
 SB SD SO 3
Do đó 
 1 · 1 ·
 SM.SE.sin MSE SM.SF.sin MSF
 S SM SE 1 2 1 S SM SF 1 2 1
 DSME = 2 = . = . = và DSMF = 2 = . = . = .
 S 1 · SC SB 2 3 3 S 1 · SC SD 2 3 3
 DSBC SC.SB.sinCSB DSCD SC.SD.sinCSD
 2 2
c) Dễ thấy K, A, J là ba điểm chung của hai mặt phẳng (a) và (ABCD) nên chúng nằm trên giao tuyến D của hai 
mặt phẳng này. Vì BD P(a) và BD Ì (ABCD) nên D PBD suy ra D PEF .
 EF SI 2 BD CO 1 EF 1
Ta có = = ; = = . Vậy = .
 BD SO 3 KJ CA 2 KJ 3
Bài 14. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD PBC và AD = 2BC . Gọi M , N lần lượt là trung 
 SP
điểm của SA và SB . Xác định giao điểm P của đường thẳng SC với mặt phẳng (DMN) và tính tỉ số .
 SC
 Lời giải
a) Trong mặt phẳng (ABCD), gọi I = ABÇCD .
Khi đó (SAB)Ç(SCD)= SI . 
Trong mặt phẳng (SAB), gọi Q = MN ÇSI .
Trong mặt phẳng (SCD), gọi P = DQ ÇSC . Ta có
 ▪ P Î DQ mà DQ Ì (DMN) suy ra P Î (DMN).
 ▪ P Î SC .
Vậy P = SC Ç(DMN). 1
 S b) Xét tam giác IAD , ta có BC P= AD suy ra BC là đường 
 2
 trung bình nên C là trung điểm DI .
 SQ SM 1
 Xét tam giác SAI , ta có MN PAB nên = = suy ra 
 SI SA 2
 M
 Q là trung điểm SI .
 N Trong tam giác SDI , ta có SC và DQ là các đường trung 
 Q
 P SP 2
 D tuyến nên P là trọng tâm. Vậy = .
 A SC 3
 B C
 I
Bài 15. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AD PBC và AD = 2BC . Gọi G là trọng tâm tam giác 
 HB
 SCD . Xác định giao điểm H của đường thẳng BG với mặt phẳng (SAC) và tính tỷ số .
 HG
 Lời giải
Gọi M là trung điểm BC . Chọn mặt phẳng phụ (SBM)É BG .
Trong mặt phẳng (ABCD), gọi I = BM Ç AC . Khi đó 
 (SBM)Ç(SAC)= SI . S
Trong mặt phẳng (SBM), gọi H = BG ÇSI . Ta có 
 ▪ H Î SI mà SI Ì (SAC) suy ra H Î (SAC).
 ▪ H Î BG .
Vậy H = BG Ç(SAC).
Gọi N là trung điểm AD , suy ra MN là đường trung bình của 
tam giác DAC nên MN PAC .
Ta có BC P= AN nên tứ giác ABCN là hình bình hành. Gọi 
 J = AC ÇBN suy ra J là trung điểm của BN . G
Trong tam giác BMN , ta có MN PIJ (do MN PAC ) và J là 
trung điểm BN nên IJ là đường trung bình, suy ra I là trung H
 A N D
điểm BM hay IB = IM .
Trong mặt phẳng (SBM), kẻ GK PSI với K Î BM .
 J K M
 I
 IM SM 3
Xét tam giác SIM , ta có GK PSI nên = = . B C
 IK SG 2
 HB IB IM 3
Xét tam giác BGK , ta có GK PHI nên = = = (do IB = IM ).
 HG IK IK 2