Tự luận Đại số Lớp 10 - Chương 4.2: Bất đẳng thức. Bất phương trình (Có đáp án)

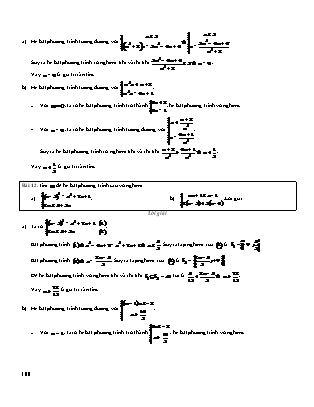
 ïì £
 ïì x £ 3 ï x 3
 ï ï
a) Hệ bất phương trình tương đương với í Û í 3m2 - 4m + 6 .
 ï m2 + 2 x ³ 3m2 - 4m + 6 ï x ³
 ï ( ) ï 2
 î îï m + 2
 3m2 - 4m + 6
 Suy ra hệ bất phương trình có nghiệm khi và chỉ khi £ 3 Û m ³ 0 .
 m2 + 2
 Vậy m ³ 0 là giá trị cần tìm.
 ì 2
 ï m x < m + 2
b) Hệ bất phương trình tương đương với íï .
 ï 2
 îï m x ³ 4m + 1
 ïì 0x < 2
 Với m = 0 , ta có hệ bất phương trình trở thành íï : hệ bất phương trình vô nghiệm.
 îï 0x ³ 1
 ïì m + 2
 ï x <
 ï 2
 Với m ¹ 0 , ta có hệ bất phương trình tương đương với í m .
 ï 4m + 1
 ï ³
 ï x
 îï m2
 m + 2 4m + 1 1
 Suy ra hệ bất phương trình có nghiệm khi và chỉ khi > Û m < .
 m2 m2 3
 1
 Vậy m < là giá trị cần tìm.
 3
Bài 12. Tìm m để hệ bất phương trình sau vô nghiệm
 ïì 2
 ï (x- 3) ³ x2 + 7x + 1 ïì mx + 1£ x- 1
 a) íï . b) íï .Lời giải
 ï ï 2(x- 3)< 5(x- 4)
 îï 2m £ 8 + 5x îï
 Lời giải
 ïì 2 2
 ï (x- 3) ³ x + 7x + 1 (1)
a) Ta có íï .
 ï £ +
 îï 2m 8 5x (2)
 8 æ 8ù
 Û 2 - + ³ 2 + + Û £ = ç- ¥ ú
 Bất phương trình (1) x 6x 9 x 7x 1 x . Suy ra tập nghiệm của (1) là S1 ç ; .
 3 èç 3ûú
 - é - ö
 2m 8 ê2m 8 ÷
 Bất phương trình (2)Û x ³ . Suy ra tập nghiệm của (2) là S2 = ;+ ¥ ÷.
 5 ëê 5 ø÷
 8 2m- 8 72
 Để hệ bất phương trình vô nghiệm khi và chỉ khi S ÇS = Æ, tức là .
 1 2 13 5 13
 72
 Vậy m > là giá trị cần tìm.
 13
 ì
 ï (m- 1)x £ - 2
 ï
b) Hệ bất phương trình tương đương với í 14 .
 ï x >
 îï 3
 ì
 ï 0x £ - 2
 ï
 Với m = 1 , ta có hệ bất phương trình trở thành í 14 : hệ bất phương trình vô nghiệm.
 ï x >
 îï 3
198 ïì - 2
 ï x £
 ï -
 Với m > 1 , ta có hệ bất phương trình tương đương với íï m 1 .
 ï 14
 ï x >
 îï 3
 - 2 14 4
 Suy ra hệ bất phương trình vô nghiệm Û £ Û - 6 £ 14(m- 1)Û m ³ .
 m- 1 3 7
 Đối chiếu điều kiện, ta chọn m > 1 .
 ïì - 2
 ï x ³
 ï -
 Với m < 1 , ta có hệ bất phương trình tương đương với íï m 1 : hệ bất phương trình luôn có nghiệm.
 ï 14
 ï x >
 îï 3
 Vậy m ³ 1 là giá trị cần tìm.
 ì
 ï 2m(x + 1)³ x + 3
Bài 13. Tìm m để hệ bất phương trình í có nghiệm duy nhất.
 ï
 îï 4mx + 3 ³ 4x
 Lời giải
 ì
 ï (2m- 1)x ³ 3- 2m
 Hệ bất phương trình tương đương với íï . 
 ï - ³ -
 îï (4m 4)x 3
 3- 2m - 3
 Giả sử hệ bất phương trình có nghiệm duy nhất thì = 
 2m- 1 4m- 4
 3 5
 Û 8m2 - 26m + 15 = 0 Û m = hoặc m = .
 4 2
 Thử lại.
 ïì æ ö
 ï ç3 ÷ 3 ì
 3 ï ç - 1÷x ³ 3- ï x ³ 3
  Với m = , ta có hệ bất phương trình trở thành í èç2 ø÷ 2 Û í Û x = 3 : thỏa mãn.
 4 ï îï x £ 3
 îï - x ³ - 3
 5 ïì 4x ³ - 2 1
  Với m = , ta có hệ bất phương trình trở thành íï Û x ³ - : không thỏa mãn.
 2 îï 6x ³ - 3 2
 3
 Vậy m = là giá trị cần tìm.
 4
Bài 14. Tìm m để hệ bất phương trình 
 ïì 7 1 3x 13
 ï x- > -
 a) íï 6 2 2 3 có nghiệm.
 ï
 ï 2 4
 îï m x + 1³ m - x
 ïì x- 2 ³ 0
 b) íï có tập nghiệm là một đoạn có độ dài bằng 5 .
 îï mx- 4 £ 0
 Lời giải
 ì ì ïì 23
 ï 7x- 3 > 9x- 26 ï 2x < 23 ï x <
a) Hệ bất phương trình tương đương với íï Û íï Û íï 2 .
 ï 2 4 ï 2 2 2 ï
 ï (m + 1)x > m - 1 ï (m + 1)x > (m + 1)(m - 1) ï 2
 îï îï îï x ³ m - 1
 23 25 5 2
 Để hệ bất phương trình đã cho có nghiệm khi và chỉ khi m2 - 1< Û m2 < Û m < .
 2 2 2
 199 5 2
 Vậy m < là giá trị cần tìm.
 2
 ïì x ³ 2
b) Hệ bất phương trình tương đương với íï .
 îï mx £ 4
 ïì x ³ 2
 Với m = 0 , ta có hệ bất phương trình trở thành íï : hệ bất phương trình có vô số nghiệm nên không thỏa 
 îï 0x £ 4
 mãn.
 ì
 ï x ³ 2
 ï
 Với m < 0 , ta có hệ bất phương trình tương đương với í 4 : hệ bất phương trình có vô số nghiệm nên 
 ï x ³
 îï m
 không thỏa mãn.
 ì
 ï x ³ 2
 ï
 Với m > 0 , ta có hệ bất phương trình tương đương với í 4 .
 ï x £
 îï m
 Điều kiện để hệ bất phương trình có tập nghiệm là một đoạn có độ dài bằng 5 khi và chỉ khi 
 4 4 4
 - 2 = 5 Û = 7 Û m = : thỏa mãn.
 m m 7
 4
 Vậy m = là giá trị cần tìm.
 7
 VAÁN ÑEÀ 03 DAÁU NHÒ THÖÙC BAÄC NHAÁT
1. Định nghĩa. Nhị thức bậc nhất (đối với x ) là biểu thức dạng ax + b , trong đó a và b là hai số cho trước và a ¹ 0 .
2. Dấu của nhị thức bậc nhất
 a) Định lí. Nhị thức bậc nhất ax + b cùng dấu với hệ số a khi x lớn hơn nghiệm và trái dấu với hệ số a khi x nhỏ 
 hơn nghiệm của nó.
 b) Bảng xét dấu
 x b
 - ¥ - + ¥ 
 a
 ax + b trái dấu a 0 cùng dấu a
3. Một số ứng dụng
 a) Giải bất phương trình tích dạng P(x)> 0 , trong đó P(x) là tích các nhị thức bậc nhất.
 Cách giải: Lập bảng xét dấu của P(x). Từ đó suy ra tập nghiệm của bất phương trình P(x)> 0 .
 P(x)
 b) Giải bất phương trình chứa ẩn ở mẫu dạng > 0 , trong đó P(x), Q(x) là tích những nhị thức bậc nhất.
 Q(x)
 P(x) P(x)
 Cách giải: Lập bảng xét dấu của . Từ đó suy ra tập nghiệm của bất phương trình > 0 .
 Q(x) Q(x)
 Chú ý: Không nên qui đồng và khử mẫu vì mẫu tham gia vào quá trình xét dấu.
 c) Giải bất phương trình chứa ẩn trong dấu giá trị tuyệt đối (GTTĐ) Tương tự như giải phương trình chứa ẩn 
 trong dấu GTTĐ, ta thường sử dụng định nghĩa hoặc tính chất của GTTĐ để khử dấu GTTĐ.
200 Bài 15. Lập bảng xét dấu các biểu thức sau
 a) - 2x + 3 . b) 4x- 12 .
 c) x2 - 4 . d) - 2x2 + 5x- 2 . 
 Lời giải
 3
a) Ta có - 2x + 3 = 0 Û x = .
 2
 Bảng xét dấu
 x 3
 - ¥ + ¥ 
 2
 - 2x + 3 + 0 -
b) Ta có 4x- 12 = 0 Û x = 3 .
 Bảng xét dấu
 x - ¥ 4 + ¥ 
 4x- 12 - 0 +
c) Ta có x2 - 4 = (x- 2)(x + 2).
 x- 2 = 0 Û x = 2 ; x + 2 = 0 Û x = - 2 .
 Bảng xét dấu
 x - ¥ - 2 2 + ¥ 
 x + 2 - 0 + | +
 x- 2 - | - 0 +
 x2 - 4 + 0 - 0 +
 é =
 êx 2 æ ö
 2 2 ç 1÷
d) Ta có - 2x + 5x- 2 = 0 Û ê 1 . Suy ra - 2x + 5x- 2 = - 2(x- 2)çx- ÷= (x- 2)(1- 2x).
 êx = èç 2ø÷
 ëê 2
 1
 x- 2 = 0 Û x = 2 ; 1- 2x = 0 Û x = .
 2
 Bảng xét dấu
 x 1
 - ¥ 2 + ¥ 
 2
 1- 2x + 0 - | -
 x- 2 - | - 0 +
 - 2x2 + 5x- 2 - 0 + 0 -
Bài 16. Lập bảng xét dấu các biểu thức sau
 - 2x + 3 4x- 12
 a) . b) .
 x- 2 x2 - 4x
 4x2
 c) x 4- x2 (x + 2) . d) 1- .
 ( ) 2
 (x + 1)
 Lời giải
 3
a) Ta có - 2x + 3 = 0 Û x = ; x- 2 = 0 Û x = 2 .
 2
 201 Bảng xét dấu
 x 3
 - ¥ 2 + ¥ 
 2
 - 2x + 3 + 0 - | -
 x- 2 - | - 0 +
 - 2x + 3
 x- 2 - 0 + || -
 4x- 12 4x- 12
b) Ta có = .
 x2 - 4x x(x- 4)
 4x- 12 = 0 Û x = 3, x = 0, x- 4 = 0 Û x = 4 .
 Bảng xét dấu
 x - ¥ 0 3 4 + ¥ 
 4x- 12 - | - 0 + | +
 x - 0 + | + | +
 x- 4 - | - | - 0 +
 4x- 12
 x2 - 4x - || + 0 - || +
 2
c) Ta có x(4- x2 )(x + 2) = x(2- x)(x + 2) .
 x = 0, 2- x = 0 Û x = 2, x + 2 = 0 Û x = - 2 .
 Bảng xét dấu
 x - ¥ - 2 0 2 + ¥ 
 x - | - 0 + | +
 2- x + | + | + 0 -
 x + 2 - 0 + | + | +
 x(4- x2 )(x + 2)
 - 0 - 0 + 0 - 
 2 2
 4x2 (x + 1) - 4x (3x + 1)(1- x)
d) Ta có 1- = = .
 2 2 2
 (x + 1) (x + 1) (x + 1)
 1
 3x + 1 = 0 Û x = - , 1- x = 0 Û x = 1, x + 1 = 0 Û x = - 1 .
 3
 Bảng xét dấu
 x 1
 - ¥ - 1 - 1 + ¥ 
 3
 3x + 1 - | - 0 + | +
 1- x + | + | + 0 -
 x + 1 - 0 + | + | +
 4x2
 1-
 2 - || - 0 + 0 - 
 (x + 1)
Bài 17. Giải các bất phương trình sau
 a) (2x- 1)(x3 - 1)£ 0 . b) x( 3x- 3)(3- x2 )£ 0 .
 Lời giải
202 æ ö2
 3 2 2 ç 1÷ 3
a) Ta có (2x- 1)(x - 1)£ 0 Û (2x- 1)(x- 1)(x + x + 1)£ 0 Û (2x- 1)(x- 1)£ 0 (vì x + x + 1 = çx + ÷ + > 0 ).
 èç 2ø÷ 4
 1
 2x- 1 = 0 Û x = , x- 1 = 0 Û x = 1 .
 2
 Bảng xét dấu
 x 1
 - ¥ 1 + ¥ 
 2
 x- 1 - | - 0 +
 2x- 1 - 0 + | +
 (x- 1)(2- 3x) + 0 - 0 +
 é1 ù
 Suy ra bất phương trình có tập nghiệm là S = ê ;1ú.
 ëê2 ûú
b) Ta có x( 3x- 3)(3- x2 )£ 0 Û x 3(x- 3)( 3 - x)( 3 + x)£ 0 .
 2
 Û - 3x(x- 3) (x + 3)£ 0 Û x = 3 hoặc x(x + 3)³ 0 .
 x = 0, x + 3 = 0 Û x = - 3 .
 Bảng xét dấu
 x - ¥ - 3 0 + ¥ 
 x - | - 0 +
 x + 3 - 0 + | +
 (x- 1)(2- 3x) + 0 - 0 +
 Suy ra x x + 3 ³ 0 Û x Î - ¥ ;- 3ùÈ é0;+ ¥ .
 ( ) ( ûú ë )
 Vậy tập nghiệm của bất phương trình là S = - ¥ ;- 3ùÈ é0;+ ¥ .
 ( ûú ë )
Bài 18. Giải các bất phương trình sau
 (x- 3)(x + 2) 1 1
 a) < 1 . b) £ .
 2 2
 x - 1 (x- 2) x + 4
 Lời giải
 (x- 3)(x + 2) (x- 3)(x + 2) x + 5
a) Ta có 0 Û > 0 .
 x2 - 1 x2 - 1 (x- 1)(x + 1)
 x + 5 = 0 Û x = - 5, x- 1 = 0 Û x = 1, x + 1 = 0 Û x = - 1 .
 Bảng xét dấu
 x - ¥ - 5 - 1 1 + ¥ 
 x + 5 - 0 + | + | +
 x + 1 - | - 0 + | +
 x- 1 - | - | - 0 +
 x + 5
 (x- 1)(x + 1) - 0 + || - || + 
 Vậy tập nghiệm của bất phương trình là S = (- 5;- 1)È(1;+ ¥ ).
 203 ïì
 2 ï x(x- 4)
 1 1 1 1 x - 4x x(x- 4) ï ³ 0
b) Ta có £ Û - ³ 0 Û ³ 0 Û ³ 0 Û íï .
 2 2 2 2 ï x + 4
 (x- 2) x + 4 x + 4 (x- 2) (x + 4)(x- 2) (x + 4)(x- 2) ï
 îï x ¹ 2
 x = 0, x- 4 = 0 Û x = 4, x + 4 = 0 Û x = - 4 .
 Bảng xét dấu
 x - ¥ - 4 0 4 + ¥ 
 x + 4 - 0 + | + | +
 x - | - 0 + | +
 x- 4 - | - | - 0 +
 x(x- 4) 
 - -
 (x + 4) || + 0 0 + 
 ù é
 Kết hợp với điều kiện xác định suy ra tập nghiệm của bất phương trình là S = (- 4;0ûÈ ë4;+ ¥ ).
Bài 19. Giải các bất phương trình sau
 a) 2x + 1 < 3x . b) x + 1 - x- 2 ³ 3 . 
 Lời giải
 1
a) Với x ³ - , ta có bất phương trình tương đương với 2x + 1 1 .
 2
 1
 Kết hợp với điều kiện x ³ - , suy ra bất phương trình có tập nghiệm là S = (1;+ ¥ ) 
 2 1
 1 1
 Với x - .
 2 5
 1
 Kết hợp với điều kiện x < - , suy ra bất phương trình vô nghiệm.
 2
 Vậy tập nghiệm của bất phương trình là S = S1 = (1;+ ¥ ).
b) Bảng xét dấu
 x - ¥ - 1 2 + ¥ 
 x + 1 - 0 + | +
 x- 2 - | - 0 +
 Từ bảng xét dấu đó ta chia ra các trường hợp sau
 Với x < - 1, ta có bất phương trình tương đương với - (x + 1)+ (x- 2)³ 3 Û - 3 ³ 3 : vô nghiệm.
 Với - 1£ x < 2 , ta có bất phương trình tương đương với (x + 1)+ (x- 2)³ 3 Û x ³ 2 .
 Kết hợp với điều kiện - 1£ x < 2 , suy ra bất phương trình vô nghiệm.
 Với x ³ 2 , ta có bất phương trình tương đương với (x + 1)- (x- 2)³ 3 Û 3 ³ 3 .
 ³ = é + ¥
 Kết hợp với điều kiện x 2 , suy ra bất phương trình có tập nghiệm là S3 ë2; )
 = = é + ¥
 Vậy tập nghiệm của bất phương trình là S S3 ë2; ).
Bài 20. Giải các bất phương trình sau
 x- 1 - 1 ( x + 1 - 2x- 1)( x + 1 - 2)
 a) ³ 0 . b) £ 0 . 
 x4 - x2 x- 1
 Lời giải
204 ïì x ¹ 0
a) Điều kiện: x4 - x2 ¹ 0 Û íï . 
 îï x ¹ ± 1
 2
 x- 1 - 1 ( x- 1 + 1)( x- 1 - 1) x- 1 - 1
 Ta có ³ 0 Û ³ 0 Û ³ 0
 x4 - x2 x4 - x2 x4 - x2
 x2 - x x(x- 1) 1
 Û ³ 0 Û ³ 0 Û ³ 0 .
 x4 - x2 x2 (x- 1)(x + 1) x(x + 1)
 Bảng xét dấu
 x - ¥ - 1 0 + ¥ 
 x + 1 - 0 + | +
 x - | - 0 +
 1 
 x(x + 1) + || - || +
 Kết hợp điều kiện xác đinh suy ra tập nghiệm bất phương trình là S = (- ¥ ;- 1)È(0;+ ¥ )\{1} .
 ì
 ì ï 1
 ï 2x- 1³ 0 ï x ³ ïì 1
 ï ï 2 ï x ³
b) Điều kiện: íï x + 1³ 0 Û íï Û íï . 
 ï ï x ³ - 1 ï 2
 ï ï ï ¹
 îï x ¹ 1 ï îï x 1
 îï x ¹ 1
 Vì x + 1 + 2x- 1 > 0, x + 1 - 2 > 0 nên bất phương trình tương đương với
 ( x + 1 - 2x- 1)( x + 1 + 2x- 1)( x + 1 - 2)( x + 1 + 2) (- x + 2)(x- 3)
 £ 0 Û £ 0 .
 x- 1 x- 1
 Bảng xét dấu
 x - ¥ 1 2 3 + ¥ 
 x- 1 - 0 + | + | +
 - x + 2 + | + 0 - | -
 x- 3 - | - | - 0 +
 (- x + 2)(x- 3) 
 x- 1 + || - 0 + 0 - 
 ù é
 Kết hợp với điều kiện xác định suy ra tập nghiệm của bất phương trình là S = (1; 2ûÈ ë3;+ ¥ ).
Bài 21. Giải và biện luận các bất phương trình sau
 3 - x
 a) (2x- 2)(x- m)> 0 . b) £ 0 .
 x- 2m + 1
 Lời giải
 2
a) Ta có 2x- 2 Û x = , x- m = 0 Û x = m . Xét ba trường hợp:
 2
 2
 Nếu m < thì ta có bảng sau
 2
 x - ¥ m 2 / 2 + ¥ 
 2x- 2 - 0 - | +
 x- m - | + 0 +
 VT + 0 - 0 +
 205 æ ö
 ç 2 ÷
 Do đó tập nghiệm của bất phương trình là S = (- ¥ ; m)Èç ;+ ¥ ÷.
 èç 2 ø÷
 æ ö2
 2 ç 2 ÷ 2
 Nếu m = thì bất phương trình trở thành 2 çx- ÷ > 0 Û x ¹ .
 2 èç 2 ø÷ 2
 ì ü
 ï 2 ï
 Do đó tập nghiệm của bất phương trình là S = ¡ \í ý .
 ï ï
 îï 2 þï
 2
 Nếu m > thì có bảng sau
 2
 x 2
 - ¥ m + ¥ 
 2
 2x- 2 - 0 + | +
 x- m - | - 0 +
 VT + 0 - 0 +
 æ ö
 ç 2 ÷
 Do đó tập nghiệm của bất phương trình là S = ç- ¥ ; ÷È(m;+ ¥ ).
 èç 2 ø÷
b) Điều kiện: x ¹ 2m- 1.
 Ta có 3 - x = 0 Û x = 3 , x- 2m + 1 = 0 Û x = 2m- 1 .
 3 + 1
 Nếu 2m- 1< 3 Û m < thì ta có bảng sau
 2
 x - ¥ 2m- 1 3 + ¥ 
 3 - x + 0 + | -
 x- 2m + 1 - | + 0 +
 VT - 0 + 0 -
 Do đó tập nghiệm của bất phương trình là S = - ¥ ; 2m- 1 È é 3;+ ¥ .
 ( ) ëê )
 3 + 1 3 - x
 Nếu 2m- 1 = 3 Û m = thì bất phương trình trở thành £ 0 Û - 1£ 0 : luông đúng.
 2 x- 3
 Đối chiếu điều kiện ta được tập nghiệm của bất phương trình là S = ¡ \{ 3} .
 3 + 1
 Nếu 2m- 1> 3 Û m > thì ta có bảng sau
 2
 x - ¥ 3 2m- 1 + ¥ 
 3 - x + 0 - | -
 x- 2m + 1 - | - 0 +
 VT - 0 + 0 -
 Do đó tập nghiệm của bất phương trình là S = - ¥ ; 3ùÈ 2m- 1;+ ¥ .
 ( ûú ( )
Bài 22. Giải và biện luận các hệ bất phương trình sau
 ì
 ïì ï 2 5
 ï mx- 1> 0 (1) ï < (1)
 a) í . b) í x- 1 2x- 1 .
 ï ï
 ï (3m- 2)x- m > 0 (2) ï - ³
 îï îï x m 0 (2)
206 Lời giải
a) Khi m = 0 thì (1) vô nghiệm nên hệ bất phương trình vô nghiệm.
 2
 Khi m = thì (2) vô nghiệm nên hệ bất phương trình vô nghiệm.
 3
 2 1 1
 Khi m ¹ 0 và m ¹ . Tùy theo giá trị của m , (1) có nghiệm x > hoặc có nghiệm x < ;
 3 m m
 m m
 (2) có nghiệm x > hoặc có nghiệm x <
 3m- 2 3m- 2
 1 m m 1 (m- 1)(m- 2)
 Ta so sánh và bằng cách lập hiệu và xét dấu của D = - = .
 m 3m- 2 3m- 2 m m(3m- 2)
 x 2
 - ¥ 0 1 2 + ¥ 
 3
 D + - + - +
 Từ đó, có các trường hợp
 m 1 1 m
 Nếu m 0 hay > . Ta có (1)Û x < và (2)Û x < .
 3m- 2 m m 3m- 2
 æ ö
 ç 1 ÷
 Do đó tập nghiệm của hệ bất phương trình là S = ç- ¥ ; ÷.
 èç mø÷
 2 m 1 1 m
 Nếu 0 và (2)Û x < .
 3 3m- 2 m m 3m- 2
 Do đó tập nghiệm của hệ bất phương trình là S = Æ.
 2 m 1 1 m
 Nếu 0 hay > . Ta có (1)Û x > và (2)Û x > .
 3 3m- 2 m m 3m- 2
 æ ö
 ç m ÷
 Do đó tập nghiệm của hệ bất phương trình là S = ç ;+ ¥ ÷.
 èç3m- 2 ø÷
 m 1 1 m
 Nếu 1£ m £ 2 thì D và (2)Û x > .
 3m- 2 m m 3m- 2
 æ ö
 ç 1 ÷
 Do đó tập nghiệm của hệ bất phương trình là S = ç ;+ ¥ ÷.
 èçm ø÷
 m 1 1 m
 Nếu m > 2 thì D > 0 hay > . Ta có (1)Û x < và (2)Û x < .
 3m- 2 m m 3m- 2
 æ ö
 ç m ÷
 Do đó tập nghiệm của hệ bất phương trình là S = ç ;+ ¥ ÷.
 èç3m- 2 ø÷
 2 5 2(2x- 1)- 5(x- 1) x- 3
b) Ta có bất phương trình (1)Û 0 .
 x- 1 2x- 1 (x- 1)(2x- 1) (x- 1)(2x- 1)
 1
 Lập bảng xét dấu vế trái thì có nghiệm 3 .
 2
 1
 Bât phương trình (2)Û x ³ m . So sánh m với các số ; 1; 3 , ta có
 2
 æ ö
 1 ç1 ÷
 Nếu m £ thì tập nghiệm của bất phương trình là S = ç ;1÷È(3;+ ¥ ).
 2 èç2 ø÷
 1
 Nếu < m < 1 thì tập nghiệm của bất phương trình là S = ém;1)È(3;+ ¥ ).
 2 ë
 207