Ôn tập kiến thức Hình học Lớp 9 - Chương 4: Hình trụ

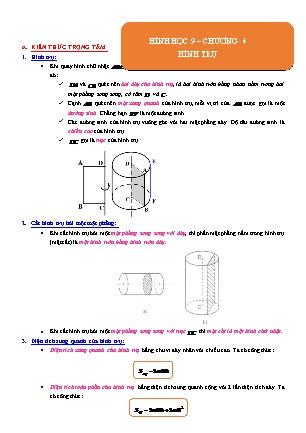
 HÌNH HỌC 9 – CHƯƠNG 4
A. KIẾN THỨC TRỌNG TÂM
1. Hình trụ: HÌNH TRỤ
 ▪ Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định, ta được một hình trụ. Khi 
 đó:
 ✓ DA và CB quét nên hai đáy của hình trụ, là hai hình tròn bằng nhau nằm trong hai 
 mặt phẳng song song, có tâm D và C .
 ✓ Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của AB được gọi là một 
 đường sinh. Chẳng hạn EF là một đường sinh.
 ✓ Các đường sinh của hình trụ vuông góc với hai mặt phẳng đáy. Độ dài đường sinh là 
 chiều cao của hình trụ.
 ✓ DC gọi là trục của hình trụ.
2. Cắt hình trụ bởi một mặt phẳng:
 ▪ Khi cắt hình trụ bởi một mặt phẳng song song với đáy, thì phần mặt phẳng nằm trong hình trụ 
 (mặt cắt) là một hình tròn bằng hình tròn đáy.
 ▪ Khi cắt hình trụ bởi một mặt phẳng song song với trục DC thì mặt cắt là một hình chữ nhật.
3. Diện tích xung quanh của hình trụ:
 ▪ Diện tích xung quanh của hình trụ bằng chu vi đáy nhân với chiều cao. Ta có công thức:
 Sxq 2 Rh
 ▪ Diện tích toàn phần của hình trụ bằng diện tích xung quanh cộng với 2 lần diện tích đáy. Ta 
 có công thức:
 2
 Stp 2 Rh 2 R 4. Thể tích hình trụ:
 ▪ Thể tích của hình trụ bằng diện tích đáy nhân với chiều cao. 
 V S.h R2h.
 (S:diện tích đáy, h:chiều cao)
B. PHƯƠNG PHÁP GIẢI VÀ CÁC DẠNG BÀI TẬP
 Dạng 1: Tính chiều cao, bán kính đáy, diện tích xung quanh, diện tích toàn phần, thể tích
 ▪ Diện tích xung quanh của hình trụ bằng chu vi đáy nhân với chiều cao. Ta có công thức:
 Sxq 2 Rh
 ▪ Diện tích toàn phần của hình trụ bằng diện tích xung quanh cộng với 2 lần diện tích đáy. 
 Ta có công thức:
 2
 Stp 2 Rh 2 R
 ▪ Thể tích của hình trụ bằng diện tích đáy nhân với chiều cao. 
 V S.h R2h.
 (S:diện tích đáy, h:chiều cao)
Bài 1: Điền đầy đủ các kết quả vào bảng sau
 Diện tích 
 Diện tích xung Thể tích 
 Bán kính đáy Chiều cao Chu vi đáy đáy 
 Hình quanh (cm
 (cm) (cm) (cm) (cm
 (cm 2 ) 3 )
 2 )
 2 20
 10 8
 16 8 
 Lời giải
Ta có bảng sau
 Diện tích 
 Diện tích xung Thể tích 
 Bán kính đáy Chiều cao Chu vi đáy đáy 
 Hình quanh (cm
 (cm) (cm) (cm) (cm
 (cm 2 ) 3 )
 2 )
 2 20 4 4 80 80 
 10 8 20 100 160 800 
 4 16 8 16 128 256 
Bài 2: Chiều cao của một hình trụ bằng bán kính của đường tròn đáy. Diện tích xung quanh của hình 
 trụ là 314 cm 2 . Tính
 a) Bán kính của đường tròn đáy.
 b) Thể tích của khối trụ. (Làm tròn kết quả đến chữ số thập phân thứ hai).
 Lời giải Theo giả thiết R h .
 S 314
 Ta có S 2 Rh 2 h2 h xq 7,07 cm.
 xq 2 2 
 Ta có V R2h h3 7,073 1110,22 cm3.
Bài 3: Một hình trụ có bán kính đáy đường tròn đáy là 16 cm, chiều cao là 9 cm. Tính
 a) Diện tích xung quanh của hình trụ.
 b) Thể tích của hình trụ. (Lấy 3,142 làm tròn kết quả đến hàng đơn vị).
 Lời giải
 2
 a) Ta có Sxq 2 Rl 23,142169 983 cm .
 b) Ta có V R2h 3,142162 9 7239 cm3.
Bài 4: Một hộp sữa ông thọ có chiều cao 12cm và đáy có đường tròn đường kính 
 8cm . Tính thể tích hộp sữa (Đơn vị cm3 , làm tròn đến số thập phân thứ nhất, 
 làm tròn đến hàng đơn vị?).
 Lời giải
 Hộp sữa ông thọ là hình trụ có chiều cao 12cm và đáy có đường tròn đường 
 kính 8cm .
 Bán kính đường tròn đáy là: r 8: 2 4 cm 
 Thể tích hộp sữa là: V r 2h .42.12 192 602,9 cm3 
Bài 5: Từ một tấm tôn hình chữ nhật có kích thước 40 cm x60 cm người ta gò thành mặt xung quanh 
 của một hình trụ có chiều cao 40 cm. Tính thể tích của khối trụ đó (đơn vị cm3 , làm tròn đến 
 số thập phân thứ nhất? làm tròn đến chữ số thập phân thứ 2).
 Lời giải
 Ta có diện tích xung quanh hình trụ bằng diện tích hình chữ nhật
 Sxq 2 R.h 40.60 2400
 30
 2 R 60 R 
 h 40
 h 40
 900
 Thể tích hình trụ là V R2.h . .60 17197,5 cm3
 2
Bài 6: Tính bán kính đáy của một hình trụ có chiều cao bằng hai lần đường kính đáy. Diện tích xung 
 quanh của hình trụ là 288 cm2 .
 Lời giải
 Vì chiều cao bằng hai lần đường kính đáy nên ta có h 4r .
 Diện tích xung quanh của hình trụ là Sxq 2 rh 288 .
 288 2 r.4r
 r 2 36
 r 6
 Vậy bán kính đáy của hình trụ là 6cm.
Bài 7: Một hình trụ có đường cao bằng đường kính đáy. Diện tích xung quanh trụ bằng 36 (cm2 ). 
 Tính thể tích hình trụ?
 Lời giải Gọi bán kính đường tròn đáy là R thì đường cao hình trụ là 2R.
 Diện tích xung quanh hình trụ là: S 2 R.h 2 R.2R 36 R 3 cm .
 Thể tích hình trụ là V .R2.h .R2.2R 2 R3 54 cm3 .
Bài 8: Một hộp sữa Ông Thọ do công ty Vinamilk sản xuất có thể tích là 293 ml. Nhà sản xuất tính 
 toán rằng, để trọng lượng của vỏ hộp là nhẹ nhất thì đường kính của đáy hộp bằng 7,2 cm (kết 
 quả đã được làm tròn) và vỏ hộp được làm từ cùng một hợp kim có độ dày như nhau tại mọi vị 
 trí. Hỏi khi đó chiều cao của hộp sữa bằng bao nhiêu? (kết quả làm tròn đến chữ số thập phân 
 thứ 2).
 Lời giải
 Ta có thể tích hộp sữa Ông Thọ là V 293ml 293 (cm3 ). Bán kính đáy hộp là 
 7,2 : 2 3,6 (cm)
 2 V 293
 Từ công thức V r h suy ra chiều cao của hộp sữa là h 7,20 (cm).
 r 2 .3,62
 Vậy chiều cao của hộp sữa là 7,20 (cm).
Bài 9: Có một lọ thủy tinh hình trụ có bán kính đáy 1dm , cao 5dm .
 a) Phải đổ vào bình bao nhiêu lít nước để mực nước trong bình cao 3dm 3,14 ?
 b) Người ta thả vào lọ một thanh sắt hình trụ cao 2dm , chìm trong nước. Mực nước trong lọ 
 dâng cao5cm . Tìm đường kính đáy của thanh sắt.
 Lời giải
 a) Số lít nước cần đổ vào bình để mực nước trong bình cao 3dm là
 V r 2h 3,14.12.3 9,42 dm3 hay 9,42 lít nước.
 b) Đổi 5cm 0,5dm .
 Thể tích nước và thanh sắt trong lọ thủy tinh là
 V r 2h 3,14.12. 3 0,5 10,99 dm3 .
 Thể tích thanh sắt là V V 10,99 9,42 1,57 dm3 .
 1,57 1 1
 Bán kính đáy của thanh sắt là r dm 5cm .
 3,14.2 4 2
 Vậy đường kính đáy của thanh sắt là 2.5 10cm2 .
Bài 10: Một hình trụ đứng có bán kính đáy là 40cm , diện tích toàn phần gấp đôi diện tích xung 
 quanh. Hỏi thùng chứa được bao nhiêu lít nước?
 Lời giải
 40 cm
 r
 h
 Vì Stp 2.Sxq 2 rh 2 r 2 2.2 rh
 2 r 2 2 rh
 r h .
 Mà r 40cm
 h 40cm
 V r 2h 3,14.402.40 200960cm3 201.
 Vậy thùng chứa được khoảng 201 lít nước.
Bài 11: Từ một tấm tôn hình chữ nhật, kích thước 50cmx189cm người ta cuộn tròn lại thành mặt 
 xung quanh của một hình trụ cao 50cm . Hãy tính
 a) diện tích tôn để làm hai đáy.
 b) thể tích của hình trụ được tạo thành.
 189 cm
 50 cm
 Lời giải
 a)Bán kính đáy:
 189
 r cm .
 2 
 Diện tích tôn để làm hai đáy là
 1892 35721
 S 2 r 2 cm2 .
 2 2 
 b) Thể tích của hình trụ là
 35721 893025
 V r 2h 50 cm3 .
 4 2 
Bài 12: Một hình trụ có chiều cao 25cm và diện tích toàn phần là 1200 cm2 . Tính thể tích của hình 
 trụ.
 Lời giải
 2 2
 Tao có: Stp 2 rh 2 r 2 rh r 1200 .
 r1 15 nhaän 
 rh r 2 600 r 2 25r 600 .
 r2 40 loaïi 
 Thể tích của hình trụ là
 V .r 2.h .152.25 5625 cm3 .
Bài 13: Một hình trụ có diện tích toàn phần bằng 432 cm2 và chiều cao bằng 5 lần bán kính đáy. 
 Chứng minh diện tích xung quanh bằng 10 lần diện tích đáy.
 Lời giải
 Ta có Sxq 2 rh . Mà h 5r (giả thuyết).
 2
 Nên Sxq 2 r.5r 10 r 10Sñ .
Bài 14: Hai cái lọ có dạng hình trụ, các kích thước như ở hình bên. Lọ nào có dung tích lớn hơn?
 Lời giải
 Gọi V1 , V2 lần lượt là thể tích của hình trụ cao và hình trụ thấp.
 Gọi R1, R2 lần lượt là bán kính của hình trụ cao và hình trụ thấp.
 2
 V1 R1 h1
 .
 2
 V2 R2 h2
 R1 r h1 3h
 Mà: ; .
 R2 2r h2 h
 2 2 2
 V1 r .3h 3 r h V 3 r h 3
 Nên: 1 .
 2 2 V 4 r 2h 4
 V2 2r h 4 r h 2
 Vậy dung tích của lọ hình trụ thấp lớn hơn.
 2
Bài 15: Một hình trụ có bán kính đáy bằng chiều cao. Cắt hình trụ này bằng một mặt phẳng chứa 
 5
 trục ta được một mặt cắt có diện tích là 80cm2 . Tính diện tích toàn phần của hình trụ.
 Lời giải
 Gọi h , r lần lượt là chiều cao và bán kính của hình trụ.
 2 2
 Vì bán kính đáy bằng chiều cao r h .
 5 5
 Mặt phẳng chứa trục cắt hình trụ là một hình chữ nhật có diện tích là 80cm2 .
 2rh 80 rh 40 .
 2 2
 Mà: r h . Nên h.h 40 h2 100 h 10cm r 4cm .
 5 5
 2 2 2
 Vậy: Stp 2 rh 2 r 2 .4.10 2 .4 112 cm .
 3
Bài 16: Một hình trụ có chiều cao bằng đường kính đáy. Biết thể tích của nó là 768 cm3 . Tính 
 4
 diện tích xung quanh của hình trụ đó.
 Lời giải
 3 3
 Ta có: V .R2.h .R2  2R  .R3 .
 4 2 3
 Theo đề ta có: V 768 .R3 768 R3 512 R 8 cm .
 2
 3 2 2 2
 Sxq 2 Rh 2 R  2R 3 R 3 .8 192 cm .
 4
Bài 17: Một hộp bánh hình trụ có chiều cao nhỏ hơn bán kính đáy là 1,5cm . Biết thể tích của hộp 
 bánh là 850 cm3 . Tính diện tích vỏ hộp.
 Lời giải
 Ta có: V .R2.h .R2. R 1,5 .R3 1,5. .R2 .
 Theo đề ta có: 
 V 850 .R3 1,5. .R2 850 R3 1,5.R2 850 0 R3 1,5.R2 850 0
 R 10
 2 
 R 10 R 8,5R 85 0 2 .
 R 8,5R 85 0 voâ nghieäm 
 Diện tích vỏ hộp là 
 2 2 2
 Stp 2 Rh 2 R 2 R R 1,5 2 R 2 R 2R 1,5 2 .10 20 1,5 370 cm .
Bài 18: Một hình trụ có diện tích toàn phần gấp hai lần diện tích xung quanh. Biết bán kính đáy hình 
 trụ là 6cm. Tính thể tích hình trụ.
 Lời giải
 2
 Ta có: Stp 2 Rh 2 R và Sxq 2 Rh .
 2 2
 Theo đề ta có: Stp 2Sxq 2 Rh 2 R 2.2 Rh 2 R 2 Rh R h .
 Do đó: V .R2.h .R2.R .R3 .63 216 cm3 .
Bài 19: Một chậu hình trụ cao 20cm . Diện tích đáy bằng nửa diện tích xung quanh, trong chậu có 
 nước cao đến 15cm . Hỏi phải thêm bao nhiêu nước vào chậu để nước vừa đầy chậu?
 Lời giải
 h
 R
 Gọi chiều cao và bán kính đáy của hình trụ lần lượt là h , R (cm).
 Thể tích của chậu, thể tích nước có trong chậu và thể tích nước cần đổ đầy chậu lần lượt là V , 
 V1 , V2 .
 1 1
 Ta có : S S R2 2 Rh R h 20cm .
 ñaùy 2 xq 2
 Thể tích của chậu là V R2.h .202.20 8000 cm3 .
 2 2 3
 Thể tích lượng nước có trong chậu là V1 R .15 .20 .15 6000 cm .
 Vậy thể tích lượng nước cần đổ vào để đầy chậu là 
 3
 V2 V V1 8000 6000 2000 cm .
Bài 20: Một hình trụ có thể tích là 200cm3 . Giảm bán kính đáy đi hai lần và tăng chiều cao lên hai 
 lần ta được một hình trụ mới. Tính thể tích của hình trụ này.
 Lời giải h
 r
 Gọi bán kính và chiều cao của hình trụ có thể tích là 200cm3 lần lượt là r , h cm .
 Ta có thể tích của hình trụ ban đầu là V r 2h 200cm3 1 .
 1
 Hình trụ mới có thể tích, bán kính và chiều cao tương ứng là V , r , h với r r ; h 2h .
 1 1 1 1 2 1
 2 1 
 2 1 1 2 1 3
 Khi đó ta có V1 r1 .h1  r .2h  r .h 200 100 cm .
 2 2 2
Bài 21: Một hình chữ nhật có chu vi và diện tích theo thứ tự là 28cm , 48cm2 . Quay hình chữ nhật 
 một vòng quanh một cạnh cố định để được một hình trụ. Tính thể tích lớn nhất của hình trụ 
 này.
 Lời giải
 Gọi chiều dài và chiều rộng của hình chữ nhật là a , b , 0 b a 14 .
 Vì hình chữ nhật có chu vi và diện tích theo thứ tự là 28cm , 48cm2 nên ta có: 
 b 14 a
 2 a b 28 b 14 a a b 0 a 8
 .
 2 a 6 
 ab 48 a 14a 48 0 b 6
 a 8
 Trường hợp 1: quay hình chữ nhật quanh cạnh cố định là chiều rộng.
 6
 8
 Hình trụ tạo thành có chiều cao: h1 6 b và bán kính r1 8 a .
 2 2 3
 Khi đó thể tích của hình trụ này là V1 .r1 .h1 .8 .6 384 cm .
 Trường hợp 2: quay hình chữ nhật quanh cạnh cố định là chiều dài.
 8
 6 Hình trụ tạo thành có chiều cao: h2 8 a và bán kính r2 6 b .
 2 2 3
 Khi đó thể tích của hình trụ này là V2 .r2 .h2 .6 .8 288 cm .
 Vậy thể tích lớn nhất có thể đạt được của hình trụ khi quay quanh cạnh cố định của hình chữ nhật là 
 384 cm3 .
Bài 22: Tính thể tích hình khối sau: (kích thước cho trong hình vẽ, làm tròn đến chữ số thập phân thứ 
 nhất).
 5mm
 R=12mm
 18mm
 R=8mm
 Lời giải
 2 2 3
 Thể tích phần thân hình trụ là V1 .r .h .8 .18 3619,1 mm .
 2 2 3
 Thể tích phần nắp hình trụ là V2 .R .h .12 .5 2261,9 mm .
 3
 Thể tích hình khối là V V1 V2 5881 mm .
Bài 23: Hình trụ có đường kính đáy bằng 4cm và chiều cao bằng đường kính đáy. Tính thể tích của 
 hình trụ (lấy 3,14 ).
 Lời giải
 d 4
 Ta có bán kính đáy là r 2 cm .
 2 2
 Vì đường kính đáy bằng chiều cao nên: h d 4 cm .
 Thể tích của hình trụ là V S.h r 2.h .22.4 50,24 cm3 .
Bài 24: Một hình trụ có bán kính đường tròn đáy là 6cm, chiều cao 9cm . 
 a) Hãy tính diện tích xung quanh của hình trụ.
 b) Tính thể tích của hình trụ (kết quả làm tròn đến hai chữ số thập phân: 3,14 ).
 Lời giải
 2
 a) Diện tích xung quanh hình trụ là Sxq 2 .r.h 2 .6.9 339,12 cm .
 b) Thể tích của hình trụ là V S.h r 2.h .62.9 1017,36 cm3 .
Bài 25: Người ta nhấn chìm hoàn toàn một tượng đá nhỏ vào một lọ thủy tinh có nước đựng hình trụ 
 có đường kính là 4cm . Nước trong lọ dâng lên 8,5mm . Hỏi thể tích tượng đá là bao nhiêu 
 cm3 ?
 Lời giải d 4
 Ta có bán kính đáy của hình trụ thủy tinh là r 2 cm .
 2 2
 Diện tích đáy của hình trụ là S .r 2 .22 12,56 cm2 .
 Thể tích của tượng đá bằng thể tích của lượng nước dâng lên so với mực nước ban đầu của lọ thuỷ tinh 
 có dạng hình trụ với diện tích đáy là 12,56cm2 và chiều cao bằng 8,5mm 0,85cm .
 V S.h 12,56.0,85 10,676 cm3 .
 Vậy thể tích của tượng đá xấp xỉ 10,676 cm3 .
Bài 26: Thùng Phuy là một vật dụng hình ống dùng để chứa và chuyên chở chất lỏng với dung tích 
 lớn. Mỗi thùng phuy có đường kính nắp và đáy là 584mm , chiều cao là 876mm .
 d = 584mm
 h = 876mm
 Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của thùng phuy.
 Lời giải
 Bán kính nắp và đáy của thùng phuy là r 292mm .
 2
 Diện tích xung quanh của thùng phuy là Sxq 2 r.h 2.292.876 511584 mm .
 2 2 2
 Diện tích toàn phần của thùng phuy là: Stp Sxq 2 r 511584 2.292 43619868704 mm .
 Thể tích của thùng phuy là:
 V r 2.h 2922.876 74691264 mm2 .
Bài 27: Một hình chữ nhật ABCD có diện tích là 2 cm2 , chu vi là 6cm và AB AD . Cho hình chữ 
 nhật này quay quanh cạnh AB một vòng ta được hình gì? Hãy tính thể tích và diện tích xung 
 quanh của hình được tạo thành.
 Lời giải
 C B
 D A