Kế hoạch dạy thêm Hình học Lớp 9 - Chương 3 - Bài 3: Góc nội tiếp

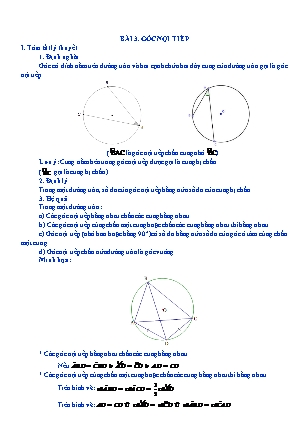
 BÀI 3. GÓC NỘI TIẾP
I. Tóm tắt lý thuyết
 1. Định nghĩa
 Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn gọi là góc 
nội tiếp.
 ( B· AC là góc nội tiếp chắn cung nhỏ B»C )
 Lưu ý: Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.
 ( B»C gọi là cung bị chắn).
 2. Định lý
 Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
 3. Hệ quả
 Trong một đường tròn:
 a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
 b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
 c) Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn 
một cung.
 d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
 Minh họa: 
 * Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
 Nếu A·BD = C·BD Þ A¼D = C»D Þ AD = CD
 * Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
 · · 1 ¼
 Trên hình vẽ: sđABD = sđACD = sđAD . 
 2
 ¼ » · ·
 Trên hình vẽ: AD = CD Û sđAD = sđCD Û sđABD = sđCAD II. Các dạng bài tập
 Dạng 1. Chứng minh hai góc bằng nhau, đoạn thẳng bằng nhau, tam giác đồng dạng
 Phương pháp giải: Dùng Hệ quả trong phần Tóm tắt lý thuyết để chứng minh hai góc bằng 
nhau, hai đoạn thẳng bằng nhau.
Bài 1: Cho đường tròn (O) và điểm I không nằm trên (O). Qua điểm I kẻ hai dây cung AB và CD 
(A nằm giữa I và B, C nằm giữa I và D).
 a) So sánh các cặp góc ·ACI và ·ABD ; C· AI và C· DB .
 b) Chứng minh các tam giác IAC và IDB đồng dạng.
 c) Chứng minh IA.IB = IC.ID.
Hướng Dẫn:
 a) HS tự chứng minh.
 b) IAC : IDB (g.g)
 c) Sử dụng kết quả câu b).
Bài 2: Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác 
A và B). Kẻ MH vuông góc với AB (H AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường 
tròn (O) vẽ hai nửa đường tròn tâm O 1, đường kính AH và tâm O2, đường kính BH. Đoạn MA và 
MB cắt hai nửa đường tròn (O1) và (O2) lần lượt tại P và Q. Chứng minh:
 a) MH = PQ;
 b) Các tam giác MPQ và MBA đồng dạng;
 c) PQ là tiếp tuyến chung của hai đường tròn (O1) và (O2).
Hướng Dẫn:
 a) MPHQ là hình chữ nhật MH = PQ
 b) Sử dụng hệ thức lượng trong tam giác vuông chứng minh được
MP.MA MQ.MB MPQ : MBA 
 · · · ·
 c) PMH MBH PQH O2QB PQ là tiếp tuyến của (O2).
 Tương tự PQ cũng là tiếp tuyến.
Bài 3: Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ 
AB. Vẽ dây MN song song với BC và gọi s là giao điểm của MN và AC. Chứng minh SM = SC và 
SN = SA.
Hướng Dẫn: Do sđ M»B = sđ M» A = sđ N»C 
 N· AS ·ANS 
 SA SN SM SC 
Bài 4: Cho tam giác ABC có ba góc nhọn, đường cao AH và nội tiếp đường tròn tâm O, đường 
kính AM.
 a) Tính ·ACM. 
 b) Chứng minh B· AH O· CA .
 c) Gọi N là giao điểm AH với (O). Tứ giác BCMN là hình gì? Vì sao? 
Hướng Dẫn:
 a) Ta có ·ACM 900 (góc nội tiếp)
 b) ta có ABH : AMC (g.g) 
 B· AH O· AC,O· CA O· AC 
 B· AH O· CA 
 c) ·ANM 900
 MNBC là hình thang
 BC / /MN sđ B»N = sđC¼M 
 C· BN B· CM nên BCMN là hình thang cân.
 Dạng 2. Chứng minh hai đường thẳng vuông góc, ba điểm thẳng hàng
Bài 1: Cho đường tròn (O) và hai dây MA, MB vuông góc với nhau. Gọi I, K lần lượt là điểm 
chính giữa của các cung nhỏ MA và MB.
 a) Chứng minh ba điểm A, O, B thẳng hàng.
 b) Gọi P là giao điểm của AK và BI. Chứng minh P là tâm đ/tròn nội tiếp tam giác MAS.
Hướng Dẫn: a) Chú ý:
 M , A, B (O) và ·AMB 900 ĐPCM.
 b) Gợi ý: Chứng minh AK và BI lần lượt là phân giác trong góc A, B của tam giác MAB.
Bài 2: Cho (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.
 a) Tam giác ABE là tam giác gì?
 b) Gọi K là giao điểm của EB với (O). Chứng minh OD  AK.
Hướng Dẫn:
 a) Chứng minh được BAE cân tại B.
 b) Chứng minh được DO//BE (tính chất đường trung bình)
 Mà AK  BE (·AKB 900 ) AK  DO 
Bài 3: Cho đường tròn (O), đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và 
SB lần lượt cắt đường tròn tại M, N. Gọi P là giao điểm của BM và AN. Chứng minh SP  AB.
Hướng Dẫn:
 Chứng minh P là trực tâm tam giác SAB.
Bài 4: Cho tam giác ABC nội tiếp đưòng tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ 
đường kính AF.
 a) Tứ giác BFCH là hình gì?
 b) Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H, M, F thẳng hàng.
 1
 c) Chứng minh OM = AH.
 2
Hướng Dẫn: a) Chứng minh được BFCH là hình bình hành.
 b) Sử dụng kết quả câu a), suy ra HF đi qua M.
 c) Chú ý: OM là đường trung bình của AHF ĐPCM.
III. Bài tập tự luyện
Bài 1: Trên cạnh huyền BC của tam giác vuông ABC về phía ngoài ta dựng hình vuông với tâm 
tại điểm O . Chứng minh rằng AO là tia phân giác của góc B·AC .
Hướng Dẫn:
 A
 B C
 O
 N M
 Vì O là tâm của hình vuông nên B·OC = 900 .
 Lại có B·AC = 900 suy ra bốn điểm A,B,O,C cùng nằm trên đường tròn đường kính BC.
 Đối với đường tròn này ta thấy B·AO = B·CO (cùng chắn B¼O ). 
 Mà B·CO = 450 Þ B·AO = 450 . Do B·AC = 900 , nên C·AO = B·AC - B·AO = 450 . 
 Vậy B·AO = C·AO , nghĩa là AO là tia phân giác của góc vuông B·AC (đpcm).
Bài 2: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H 
thuộc BC ). Chứng minh rằng B·AH = O·AC .
Hướng Dẫn:
 A
 O
 H
 B C
 D E
 Kẻ đường kính AE của đường tròn (O). Ta thấy A·CE = 900 (góc nội tiếp chắn nửa đường 
tròn). Từ đó O·AC + A·EC = 900 (1). Theo gt bài ra, ta có: B·AH + A·BC = 900 (2). Lại vì A·EC = A·BC (cùng chắn A¼C ) (3).
 Từ (1),(2) và (3) suy ra B·AH = O·AC (đpcm).
Lưu ý: Cũng có thể giải bài toán theo hướng sau: Gọi D là giao điểm của tia AH với đường tròn 
 » »
(O), chứng tỏ tứ giác BDEC là hình thang cân. Từ đó suy ra sđBD = sđCE , dẫn đến 
B·AD = C·AE , hay B·AH = O·AC .
Bài 3: Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung B¼C không chứa A ta lấy điểm 
P bất kỳ (P khác B và P khác C ). Các đoạn PA và BC cắt nhau tại Q .
 a) Giả sử D là một điểm trên đoạn PA sao cho PD = PB . Chứng minh rằng DPDB đều.
 b) Chứng minh rằng PA = PB + PC .
 1 1 1
 c) Chứng minh hệ thức = + .
 PQ PB PC
Hướng Dẫn:
 A
 O
 D
 B Q C
 P
a)Trước tiên ta nhận thấy rằng tam giác PBD cân tại P . 
 Mặt khác, B·PD = B·PA = B·CA = 600 (hai góc nội tiếp cùng chắn A»B của đường tròn (O)).
 Vậy nên tam giác PDB đều.
b)Ta đã có PB = PD , vậy để chứng minh PA = PB + PC 
 ta sẽ chứng minh DA = PC . 
 Thật vậy, xét hai tam giác BPC và BDA có: 
 BA = BC (giả thiết), 
 BD = BP (do tam giác BPD đều). 
 Lại vì A·BD + D·BC = 600 , P·BC + D·BC = 600 
 Nên A·BD = P·BC . Từ đó DBPC = DBDA (c.g.c),
 Dẫn đến DA = PC (đpcm).
c) Xét hai tam giác PBQ và PAC Ta thấy B·PQ = 600 , A·PC = A·BC = 600 (hai góc nội tiếp cùng chắn cung A¼C ) 
 Suy ra B·PQ = A·PC,P·BQ = P·BC = P·AC (hai góc nội tiếp cùng chắn P¼C ). 
 PQ PC
 Từ đó DPBQ : DPAC (g.g) Þ = , 
 PB PA
 Hay PQ.PA = PB.PC . 
 Theo kết quả câu b , ta có PA = PB + PC nên PQ (PB + PC ) = PB.PC . 
 1 1 1
 Hệ thức này tương đương với = + (đpcm).
 PQ PB PC
Bài 4: Cho tam giác ABC nội tiếp trong đường tròn (O) . Đường phân giác trong góc A cắt đường 
tròn ngoại tiếp tam giác tại D . Gọi I là tâm vòng tròn nội tiếp tam giác ABC . Chứng minh 
DB = DC = DI
Hướng Dẫn:
 A
 I O
 B C
 D
 Ta luôn có DB = DC do AD là phân giác trong góc A . 
 Ta sẽ chứng minh tam giác DIB cân tại D . 
 Thật vậy ta có: I·BD = I·BC + C·BD . 
 Mặt khác C·BD = C·AD (Góc nội tiếp chắn cung CD ) 
 Mà B·AD = C·AD , I·BC = I·BA (Tính chất phân giác) 
 Suy ra I·BD = A·BI + B·AI . 
 Nhưng B·ID = A·BI + B·AI (Tính chất góc ngoài). 
 Như vậy tam giác BDI cân tại D Þ DB = DI = DC
Bài 5: Cho tam giác nhọn ABC nội tiếp đường tròn (O) và AB < AC . Lấy điểm M thuộc cung 
 BC AC AB
BC không chứa điểm A . Vẽ MH,MK ,MI lần lượt vuông góc với = +
 MH MK MI
Hướng Dẫn: Trong bài toán có các tỷ số độ dài 
 ta nghỉ đến các tam giác đồng dạng và định lý Thales. 
Cách 1: Dựng đường thẳng qua A song song với BC cắt (O) tại N . 
 GọiE là giao điểm của BC và MN
 Ta có: AB = NC . 
 · · 1 æ» ¼ ö 1 æ¼ ¼ ö ·
 Ta có BME º BMN = sđçAB + AN ÷= sđçNC + AN ÷= AMC , 
 2 èç ø÷ 2 èç ø÷
 M·BC = M·AC Þ DBME : DAMC 
 Và MH,MK là hai đường cao tương ứng 
 AC BE
 Nên: = , 
 MK MH
 AB CE
 Chứng minh tương tự ta cũng có: = . 
 MI MH
 BC AC AB
 Cộng hai đẳng thức trên ta có: = +
 MH MK MI
Cách 2: Ta thấy MH,MI là các đường cao của tam giác MBC,MAB 
 Nhưng hai tam giác này không đồng dạng với nhau. 
 Điều này giúp ta nghỉ đến việc lấy một điểm E trên cạnh BC sao cho B·MA = D·MC để 
tạo ra tam giác đồng dạng nhưng vẫn giữ được hai đường cao tương ứng. (Phần lời giải xin dành 
cho bạn đọc).
Bài 6:Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B . Vẽ cát tuyến CAD vuông góc 
với AB . Tia CB cắt (O’) tại E, tia BD cắt (O) tại F. Chứng minh rằng: 
 a) ∠CAF = ∠DAE 
 b) AB là tia phân giác của ∠EAF
 c) CA.CD = CB.CE 
 d) CD2 = CB.CE + BD.CF
Hướng dẫn Vì CD ⊥ AB => ∠CAB = 90o Mà ∠CAB = 1/2 sđ B»C => sđ B»C = 180o 
 Vậy ba điểm B, O, C thằng hàng. 
 Chứng minh tương tự ta có B, O’, D thẳng hàng. 
a) Chứng minh ∠CAF = ∠DAE 
 Trong (O) ta có: ∠CAF = ∠CBF (góc nội tiếp cùng chắn cung CF ) 
 Trong (O’) ta có: ∠DAE = ∠DBE (góc nội tiếp cùng chắn cung DE ) 
 Mà ∠CBF = ∠DBE (đối đỉnh) 
 => ∠CAF = ∠DAE . 
b) AB là tia phân giác của ∠EAF
 Nối CF và DE ta có: ∠CFB = 90o (góc nội tiếp chắn nửa đường tròn (O)) 
 ∠BED = 90o (góc nội tiếp chắn nửa đường tròn (O’)) 
 Xét ΔCFB và ΔDEB có: 
 ∠CFB = ∠BED = 90o 
 ∠CBF = ∠DBE (đối đỉnh) 
 => ∠FCB = ∠EDB 
 Mặt khác: ∠FAB = ∠FCB (góc nội tiếp (O) cùng chắn cung FB ) 
 ∠EAB = ∠EDB (góc nội tiếp (O’) cùng chắn cung EB ) 
 => ∠FAB = ∠EAB hay AB là phân giác của góc ∠EAF . 
c) Chứng minh CA.CD = CB.CE 
 Xét ΔCAE và ΔCBD có: 
 ∠C chung 
 ∠CEA = ∠BDA (góc nội tiếp (O’) cùng chắn cung AB) 
 => ΔCAE ∼ ΔCBD (g.g) => CA/CB = CE/CD hay CA.CD = CB.CE (1) 
d) Chứng minh CD2 = CB.CE + BD.CF
 Chứng minh tương tự câu c) ta có: DA.DC = DB.DF (2) 
 Từ (1) và (2) suy ra: 
 CA.CD + DA.DC = CB.CE + DB.DF 
 ⇔ (CA + DA)CD = CB.CE + DB.DF ⇔ CD2 = CB.CE + DB.DF
Bài 7: Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung 
AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh rằng: 
 a) MA.MB = MC.MD. 
 b) Tứ giác ABEC là hình thang cân. 
 c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O). 
Hướng Dẫn:
a) Chứng minh MA.MB = MC.MD. 
 Xét ΔAMC và ΔDMB có: 
 ∠ACD = ∠ABD (góc nội tiếp cùng chắn cung AD) 
 ∠AMC = ∠BMD = 90o (gt) 
 => ΔAMC ∼ ΔDMB (g.g) 
 => MA/MD = MC/MB => MA.MB = MC.MD 
b) Chứng minh tứ giác ABEC là hình thang cân. 
 Vì ∠DCE = 90o (góc nội tiếp chắn nửa đường tròn) 
 => CD ⊥ CE CD ⊥ AB (gt) => AB // CE. 
 => Tứ giác ABEC là hình thang (1). 
 Mặt khác: CE và AB là hai dây song song của đường tròn (O) chắn hai cung AC và BE
 => A»C B»E A»E B»C A· BE B· AC (2)
 Từ (1) và (2) suy ra tứ giác ABEC là hình thang cân. 
c) Tổng có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O). 
 Ta có A»E B»C (cmt) => EA = BC . 
 Mặt khác: ∠DAE = 90o (góc nội tiếp chắn nửa đường tròn)