Kế hoạch dạy thêm Hình học Lớp 9 - Chương 2 - Bài 6: Tính chất hai tiếp tuyến cắt nhau
I.TÓM TẮT LÝ THUYẾT
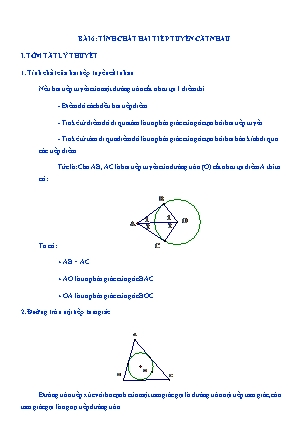
1. Tính chất của hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì
- Điểm đó cách đều hai tiếp điểm
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
Tức là: Cho AB, AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại điểm A thì ta có:
Ta có:
+ AB = AC
+ AO là tia phân giác của góc BAC
+ OA là tia phân giác của góc BOC
2. Đường tròn nội tiếp tam giác
Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn
Tâm của đường tròn nôi tiếp tam giác là giao điểm của các đường phân giác của các góc trong tam giác
3. Đường tròn bàng tiếp tam giác
Đường tròn tiếp xúc với 1 cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác
Mỗi tam giác có 3 đường tròn bàng tiếp tam giác
Tâm của đưuòng tròn bàng tiếp tam giác góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C hoặc là giao điểm của đường phân giác góc A và đường phân giác ngoài tại B (hoặc C)
Tóm tắt nội dung tài liệu: Kế hoạch dạy thêm Hình học Lớp 9 - Chương 2 - Bài 6: Tính chất hai tiếp tuyến cắt nhau
BÀI 6: TÍNH CHẤT HAI TIẾP TUYẾN CẮT NHAU I.TÓM TẮT LÝ THUYẾT 1. Tính chất của hai tiếp tuyến cắt nhau Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì - Điểm đó cách đều hai tiếp điểm - Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến - Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm Tức là: Cho AB, AC là hai tiếp tuyến của đường tròn (O) cắt nhau tại điểm A thì ta có: B 1 1 O A 2 2 Ta có: C + AB = AC + AO là tia phân giác của góc BAC + OA là tia phân giác của góc BOC 2. Đường tròn nội tiếp tam giác A O B C Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn Tâm của đường tròn nôi tiếp tam giác là giao điểm của các đường phân giác của các góc trong tam giác 3. Đường tròn bàng tiếp tam giác A B C Đường tròn tiếp xúc với 1 cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác Mỗi tam giác có 3 đường tròn bàng tiếp tam giác Tâm của đưuòng tròn bàng tiếp tam giác góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C hoặc là giao điểm của đường phân giác góc A và đường phân giác ngoài tại B (hoặc C) II. CÁC DẠNG BÀI TẬP Dạng 1: Chứng minh hai đoạn thẳng bằng nhau, hai đường thẳng song song, hai đường thẳng vuông góc Phương pháp giải: Dùng tính chất của hai tiếp tuyến cắt nhau. Bài 1:Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau ở A a. Chứng minh AO là trung trực của đoạn thẳng BC b. Vẽ đường kính CD của (O). Chứng minh BD // AO A B C O D HD: a. Theo tính chất hia tiếp tuyến cắt nhau ta có: AB = AC A thuộc đường trung trực của BC Lại có: OB OC O thuộc đường trung trực của BC Vậy AO là đường trung trực của đoạn BC b. Ta có AO BC; DB BC BD // AO (đpcm). Bài 2: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là hai tiếp điểm). a) Chứng minh: OA MN. b) Vẽ đường kính NOC. Chứng minh: MC // AO. c) Tính độ dài các cạnh của AMN biết OM = 3cm, OA = 5cm. HD: M C O H A N a. Gọi H là giao điểm của OA và MN Có AMN cân tại A có AH đồng thời là đường cao AH MN OA MN b. Chưng sminh được AMON nội tiếp ·AOM M· NA (1) 1 mà M· NA M· CN sđ cung MN (2) 2 Từ 1,2 ·AOM M· CN(3) Tam giác OMC cân tại O O· CM O· MC N· CM O· MC(4) Từ 3,4 ·AOM O· MC OA / /MC ( 2 góc ở vị trí slt). c. Tính được AM AN 4cm ( định lý Pitago) Áp dụng HTL vào tam giác OMA vuông tại M 12 24 MH.OA OM.AM MH cm MN 2MH cm . 5 5 Bài 3: Cho đường tròn (O; R) và một điểm A nằm ngoài (O). Từ A kẻ hai tiếp tuyến AM, AN của (O) (M, N là hai tiếp điểm). a) AMN là gì ? Vì sao ? b) Đường thẳng vuông góc với OM tại O cắt đường thẳng AN tại P. Chứng minh: AP = PO. c) Gọi H là giao đểm của AO và MN. Chứng minh: OH . OA = R2. HD: M H O A P N a) Ta có: AM AN (Tính chất hai tiếp tuyến cắt nhau) AMN cân tại A . b) Vì PO OM ; AM OM PO P AM M· AO ·AOP slt Mà M· AO ·AOP (Tính chất hai tiếp tuyến cắt nhau) Do đó ·AOP O· AP APO cân tại P AP OP . Bài 4: Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A khác B và C). Qua O, kẻ tia Ox song song với AC, tia Ox cắt AB tại D. a) Chứng minh: OD AB và từ đó suy ra D là trung điểm của AB. b) Tiếp tuyến tại B của (O) cắt tia Ox tại E. Chứng minh: EA cũng là tiếp tuyến của (O) c) Tia CA cắt tia BE tại F. Chứng minh: tia CE đi qua trung điểm I của của đường cao AH của ABC. HD: x F A E I D B C H O a) BAC nội tiếp O có BC là đường kính BAC vuông tại A AC AB , mà AC P OD OD AB Xét O có: AB là dây không đi qua tâm , OD thuộc đường kính, OD AB D là trung điểm của AB . b) AOB cân tại O có OD AB OD là đường phân giác của ·AOB ·AOE B· OE Xét OAE và OBE có: OA OB; ·AOE B· OE;OE chung AOE BOE c.g.c O· AE O· BE , mà O· BE 900 O· AE 900 OA EA Do đó EA là tiếp tuyến của O . c) EBA có EA EB EAB cân tại E E· AB E· BA Mà E· AB E· AF 900 ; E· BA E· FA 900 E· AF E· FA AEF cân tại A EA EF , mà EA EB EB EF . Xét BEC có IH P EB BC , theo hệ quả định lí Ta lét ta có: IC IH CE EB Xét ECF có EF P IA BC , theo hệ quả định lí Ta lét ta có: IC IA CE EF Do đó IH IA . Bài 5: Từ 1 điểm A nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB, AC với đường tròn. Đường thẳng vuông góc với OB tại O cắt AC tại N. Đường thẳng vuông góc với OC tại O cắt AB tại M a. Chứng minh rằng tứ giác AMON là hình thoi b. Điểm A cách O một khoảng là bao nhiêu để MN là tiếp tuyến của đường tròn (O) B M 1 H 2 O A N C HD : ON // AM a. Ta có AMON là hình bình hành AN // OM ˆ ˆ Lại có A1 A2 AMON là hình thoi MN OA; HA HO b. Để MN là tiếp tuyến của đường tròn (O) thì OH = R hay OA = 2OH = 2R. Vậy OA = 2R Bài 6: Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B ) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và By lần lượt tại C và D a. Chứng minh rằng COD : AMB b. Chứng minh MC. MD không đổi khi M di động trên nửa đường tròn c. Cho biết OC = BA = 2R. Tính AC và BD theo R C M D A B O HD : a. Ta có COD : AMB(gg) b. Theo câu a ta có : COD : AMB MC.MD OM 2 (dpcm) c. Xét AOC(Aˆ 900 ) OC 2 OA2 AC 2 ( pytago) AC R 3(cm) R 3 Ta lại có : AC.BD MC.MD R2 BD (cm) . 3 Bài 7:Cho tam giác ABC vuông tại A, đường cao AH. Vẽ (A, AH), kẻ các tiếp tuyến BD và CE với đường tròn (A) (D, E là các tiếp điểm khác H) a. Chứng minh rằng: D, A, E thẳng hàng b. DE là tiếp tuyến của đường tròn với đường kính BC HD: B D H O 2 1 3 A 4 C E a)Theo tính chất của hai tiếp tuyến cắt nhau, ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 0 Ta có: A1 A2 ; A 3 A4 A1 A2 A 3 A4 2BAC 180 D, A, E thẳng hàng. b. Gọi O là trung điểm của BC DBEC là hình thang ( DB,CE ED ) OA là đường trung bình của hình thang DBEC OA// DB // EC OA DE BC Hay DE là tiếp tuyến của đường tròn (O; ) 2 Bài 8:Từ điểm A nằm ngoài đường tròn O; R kẻ hai tiếp tuyến AB, AC (với B và C là các tiếp điểm). Kẻ BE AC;CF AB E AC, F AB , BE CF H. a) Chứng minh tứ giác BOCH là hình thoi b) Chứng minh ba điểm A, O, H thẳng hàng c) Xác định vị trí điểm A để H nằm trên (O). A F E H B C O HD: b) Ta có A, H, O cùng nằn trên đường vuông góc với BC nên thẳng hàng nhau c) Để H O thì OH OC COˆA 600 Dạng 2: Chứng minh tiếp tuyến, tính độ dài, tính số đo góc Phương pháp giải: Ta sử dụng các kiến thức sau Tính chất của hai tiếp tuyến cắt nhau Khái niệm đường tròn nội tiếp, bàng tiếp Hệ thức lượng về cạnh và góc trong tam giác vuông Bài 1: Cho đường tròn (O ; R) đường kính AB. Một tiếp tuyến tại M của (O) cắt hai tiếp tuyến Ax, By theo thứ tự tại C và D. Chứng minh: đường tròn đường kính CD tiếp xúc với AB. HD: D I M C A O B Gọi I là trung điểm CD ACDB là hình thang ( AC PBD ) có IC ID(gt);OA OB R Suy ra OI là đường trung bình của hình thang OI P AC PBD Mà AC AB, BD AB(gt) OI AB Suy ra đường tròn đk CD tiếp xúc với AB. Bài 2: Cho (O ; 3cm) và điểm A sao cho OA = 5cm. Kẻ cac tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Gọi H là giao điểm của AO và BC. a) Tính độ dài OH. b) Qua điểm M bắt kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn, cắt AB, AC theo thứ tự tại D và E. Tính chi vi ADE. HD: B D A H O M E C a) Vì OB OC nên OBC cân tại O , màOA là tia phân giác B· OC (Tính chất hai tiếp tuyến cắt nhau). OA BC Xét OAB vuông tại B , đường cao BH . Theo hệ thức lượng trong tam giác vuông ta có: OB2 OH.OA hay32 OH.5 OH 1,8cm b) Ta có: C ADE AD DE AE AD DM ME AE Mà DM DB;ME EC; AB AC (Tính chất tiếp tuyến cắt nhau)
File đính kèm:
 ke_hoach_bai_day_them_hinh_hoc_lop_9_chuong_2_bai_6_tinh_cha.doc
ke_hoach_bai_day_them_hinh_hoc_lop_9_chuong_2_bai_6_tinh_cha.doc

