Kế hoạch dạy thêm Hình học Lớp 9 - Chương 2 - Bài 4: Vị trí tương đối của đường thẳng và đường tròn

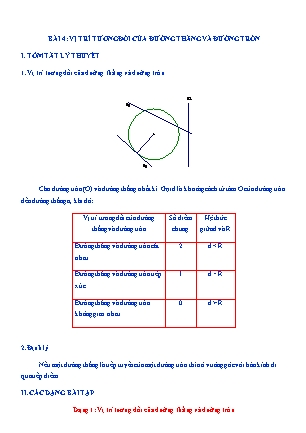
 BÀI 4: VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
I. TÓM TẮT LÝ THUYẾT 
1. Vị trí tương đối của đường thẳng và đường tròn
 d2
 d1
 d3
 Cho đường tròn (O) và đường thẳng a bất kì. Gọi d là khoảng cách từ tâm O của đường tròn 
đến đường thẳng a, khi đó:
 Vị trí tương đối của đường Số điểm Hệ thức 
 thẳng và đường tròn chung giữa d và R
 Đường thẳng và đường tròn cắt 2 d < R
 nhau
 Đường thẳng và đường tròn tiếp 1 d = R
 xúc
 Đường thẳng và đường tròn 0 d > R
 không giao nhau
2. Định lý
 Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi 
qua tiếp điểm.
II. CÁC DẠNG BÀI TẬP
 Dạng 1: Vị trí tương đối của đường thẳng và đường tròn Bài 1: Trên mặt phẳng tọa độ cho điểm I(–3 ; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì 
đường tròn đó có vị trí tương đối như thế nào đối với cac trục tọa độ ?
HD:
 Kẻ IA  Ox .Do IA 2 R nên đường tròn tâm (I) tiếp xúc với trục hoành.
 Kẻ IB  Oy .Do IB 3 R nên đường tròn tâm (I) và trục tung không giao nhau.
Bài 2: Cho đường thẳng a. Tâm I của tất cả các đường tròn có bán kính 5cm và tiếp xúc với đường 
thẳng a nằm trên đường nào ?
HD:
 Tâm I của các đường tròn có bán kính 5cm và tiếp xúc với đường thẳng a nằm trên hai 
đường thẳng d và d 'song song với a và cách a là 5cm Dạng 2: Dạng toán liên quan đến tính độ dài
Phương pháp giải: Ta nối tâm với tiếp điểm để vận dụng định lý về tính chất của tiếp điểm và sử 
dụng định lý pyatago.
Bài 1: Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với 
đường tròn trong đó B là tiếp điểm. Tính độ dài đoạn AB
 B
 A 4 6 O
HD:
 Ta có ABC vuông tại B AB 8cm
 8
Bài 2: Cho đường tròn (O;R) và dây AB R . Vẽ một tiếp tuyến song song với AB, cắt các tia 
 5
OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN
HD :
 Tiếp tuyến MN, tiếp điểm K. Vì AB // MN nên OH  AB
 3 4 4
 Ta tính được OH R KN R S R2
 5 3 OMN 3 Bài 3:Cho đường tròn (O; 2 cm) và một điểm A chạy trên đường tròn đó. Từ A vẽ tiếp tuyến xy. 
Trên xy lấy một điêm M sao cho AM 2 3 cm . Hỏi điểm M di động trên đường nào khi A chạy 
trên (O)?
 A
 2 3
 2
 M O
HD:
 Tính được OM 4 M di chuyển trên O;4cm 
Bài 4:Cho đường tròn (O; 2 cm) và điểm A ngoài (O). Từ A kẻ cát tuyến với (O), cắt (O) tại B và 
C. Cho biết AB = BC và kẻ đường kính COD, tính độ dài đoạn thẳng AD.
 A
 B
 2
 D
 O 2
 C
HD:
 Chứng minh được OB là đường trung bình của CDA AD 4cm Bài 5: Cho điểm M cách đường thẳng xy 6cm, vẽ đường tròn (M;10)
 a. Chứng minh rằng đường tròn tâm M và đường thẳng xy cắt nhau
 b. Gọi hai giao điểm là P và Q. Tính PQ
 M
 x y
 P H Q
HD:
 a. Kẻ MH  xy H MH là khoảng cách từ M đến xy
 MH 6cm
 MH R xy cắt (0;10cm) tại P và Q
 R 10cm
 1
 b. Ta có MH  PQ HP HQ PQ (Quan hệ vuông góc đường kính và dây) 
 2
 PQ 2.HQ
 Xét MHQ(Hˆ 900 ) HQ 8cm(HQ 0) PQ 16(cm)
Bài 6: Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). 
 a)Chứng minh đường tròn (A) có hai giao điểm với đường thẳng xy. 
 b)Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
HD:
 a) Kẻ AH  xy .Ta có AH AC tức là d R nên đường tròn (A) và đường thẳng xy cắt 
nhau. Do đó (A) có hai giao điểm với xy .
 AH 2 HC 2 AC 2
 b) Trong VAHC vuông tại H có: 122 HC 2 132
 HC 2 169 144 25 HC 5
 Do AH là một phần của đường kình; BC là dây cung; Mà AH  BC
 Nên H là trung điểm BC (quan hệ đường kính và dây cung)
 Vậy BC 2.HC 2.5 10(cm)
Bài 7: Cho đường tròn (O; 2cm). Một đường thẳng đi qua điểm A nằm bên ngoài đường tròn và cắt 
đường tròn tại B và C, trong đó AB = BC. Kẻ đường kính COD. Tính AD.
HD:
 Trong tam giác ACD có: O là trung điểm CD ; B là trung điểm AC
 Nên OB là đường trung bình ACD
 1
 Do đó OB AD mà OB 2cm
 2
 Vậy AD 2.2 4cm
Bài 8: Cho hình thang ABCD ( Aµ Dµ 900 ), AB = 4cm, BC= 13cm, CD = 9cm.
 a) Tính độ dài AD.
 b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
HD: a) Tính độ dài AD
 Hạ BK  CD
 Dễ dàng chứng minh được tứ giác ABKD là hình chữ nhật
 BC 2 BK 2 KC 2
 Trong tam giác VBKC vuông tại K có: BK 2 132 52 169 25 144
 BK 12cm
 Vậy AD 12cm
 b) Chứng minh rằng AD tiếp xúc với đường tròn có đường kính là BC.
 Gọi I là trung điểm BC
 BC
 Đường tròn tâm (I) đường kính BC có bán kính R 6,5cm
 2
 Kẻ IH  AD Khoảng cách d từ I đến AD bằng IH ta có:
 AB CD 4 9
 d IH 6,5cm
 2 2
 Do d R nên đường tròn (I) tiếp xúc với AD
Bài 9: Cho (O; R), bán kính OA, dây CD là đường trung trực của OA.
 a) Tứ giác OCAD là hình gì ? Vì sao ?
 b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính CI. 
HD:
 a) Gọi H là giao điểm của OA và CD .
 Có: OA  CD nên CH HD
 Xét tứ giác OCAD có:OH HA;CH HD nên tứ giác OCAD là hình bình hành. màOA  CD nên tứ giác OCAD là hình thoi
 b) Dễ dàng chứng minh được VOCA là tam giác đều.
 nên ·AOC 600
 Trong VOCI vuông tại C có:CI OC.tan 600 R 3
Bài 10: Cho hình vuông ABCD, trên đường chéo BD lấy điểm I sao cho BI = BA. Đường thẳng kẻ 
qua I vuông góc với BD cắt AD ở E.
 a. So sánh AE, EI, ID
 b. Xác định vị trí tương đối của đường thẳng BD với đường tròn (E;EA)
 A B
 E
 I
 1
 D C
HD :
 a. Ta có AEB IEB(ch cgv) AE EI(1)
 ˆ 0 ˆ 0
 EID(I 90 ), D1 45 vuông cân IE ID(2)
 Từ (1)(2) AE EI ID
 b. Ta lại có EI EA I (E; EA) R EI
 Mặt khác : EI  BD d EI d R đường thẳng BD tiếp xúc với (E :EA)
Bài 11:Cho nửa đ/tròn tâm O, đường kính AB. M là 1 điểm thuộc nửa đường tròn, qua M vẽ tiếp 
tuyến với nửa đường tròn. Gọi D và C theo thứ tự là các hình chiếu của A và B trên tiếp tuyến ấy
 a. Chứng minh rằng M là trung điểm của CD
 b. Chứng minh AB =BC + AD
 c. Giả sử AOˆM BOˆM , gọi E là giao điểm của AD với nửa đường tròn. Xác định dạng của 
tứ giác BDCE d. Xác định vị trí của điểm M trên nửa đường tròn sao cho tứ giác ABCD có diện tích lớn 
nhất. Tính diện tích đó theo bán kính của nửa đường tròn đã cho.
 D
 E
 M
 C
 A
 O B
HD:
 a. Hình thang ABCD có AO = OB, OM // AD // BC M là trung điểm của CD
 b. Ta có: AB = 2OM = BC + AD
 c. Tứ giác BDCE là hình chữ nhật vì có 3 góc vuông
 AD BC
 d. S .BE OM.BE OM.AB 2R2 maxS 2R2  OM  AB
 ABCD 2 ABCD
Bài 12: Cho đoạn thẳng AB và trung điểm O của AB. Trên cùng một nửa mặt phẳng bờ AB vẽ tia 
Ax, By vuông góc với AB. Trên các tia Ax và By lấy theo thứ tự hai điểm C và D sao cho 
COˆD 900 , kẻ OH  CD
 a. Chứng minh rằng H thuộc đường tròn tâm O đường kính AB.
 b. Xác định vị trí tương đối của CD với đường tròn (O)
 D
 H
 C
 B
 A O
HD :
 a)Kéo dài DO cắt AC ở E, ta có AOE BOD(gcg) Eˆ Dˆ;OD OE OHD OAE(ch gn)
 OH OA OB H (O; AB)
 b. Ta có H thuộc đường tròn (O), CD  OH tại H khoảng cách từ O đến CD bằng bán 
kính của (O). Vậy CD tiếp xúc với (O) tại H.
Bài 9: Cho điểm A cách đường thẳng xy một khoảng 12 cm
 a. Chứng minh A;13cm cắt đường thẳng xy tại hai điểm phân biệt
 b. Gọi hai giao điểm của A;13cm với xy là B, C. Tính độ dài đoạn thẳng BC
 B H C
 x y
 A
HD :
 a) Kẻ AH  xy AH 12cm R (A) cắt xy tại hai điểm B và C
 b) Tính được BC 2.HC 10cm.
Bài 10: Cho nửa đường tròn (O) đường kính AB. Lấy điểm C là điểm thuộc (O) và gọi d là tiếp 
tuyến qua C với với (O). Kẻ AE và BF cùng vuông góc với d; CH vuông góc với AB
 a. Chứng minh CE CF và CH 2 AE.BF
 b. Khi C di chuyển trên một nửa đường tròn, tìm vị trí của điểm C để EF có độ dài lớn 
nhất
 F
 C
 E
 A O B
 H