Kế hoạch dạy thêm Hình học Lớp 9 - Chương 1 - Bài 2: Tỉ số lượng giác của góc nhọn

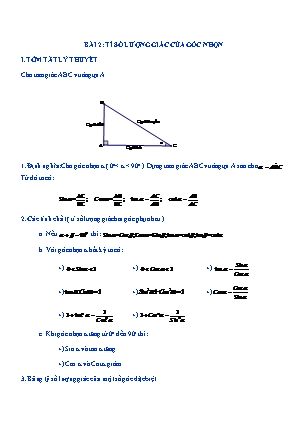
 BÀI 2: TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN 
I.TÓM TẮT LÝ THUYẾT
Cho tam giác ABC vuông tại A
 B
 Cạnh huyền
 Cạnh đối
 α
 A Cạnh kề C
1.Định nghĩa: Cho góc nhọn α ( 00< α < 900 ). Dựng tam giác ABC vuông tại A sao cho ABˆC . 
Từ đó ta có:
 AC AB AC AB
 Sin = ; Cos = ; tan ; cot 
 BC BC AB AC
2. Các tính chất ( tỉ số lượng giác hai góc phụ nhau )
 a. Nếu  900 thì: Sin =Cos;Cos =Sin;tan =cot;tan =cot 
 b. Với góc nhọn α bất kỳ ta có: 
 Sin 
 +) 0 Sin 1 +) 0 Cos 1 +) tan 
 Cos 
 Cos 
 +) tan .Cot 1 +) Sin2 Cos2 1 +)Cot 
 Sin 
 1 1
 +) 1 tan2 +) 1 Cot 2 
 Cos2 Sin2 
 c. Khi góc nhọn α tăng từ 00 đến 900 thì: 
 +) Sin α và tan α tăng
 +) Cos α và Cot α giảm
3. Bảng tỷ số lượng giác của một số góc đặc biệt 300 450 600
 Sin α 1 2 3
 2 2 2
 Cos α 3 2 1
 2 2 2
 tan α 3 1 3
 3
 cot α 3 1 3
 3
II. CÁC DẠNG BÀI TẬP
 Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp giải: Sử dụng các kiến thức trong phần tóm tắt lý thuyết
Bài 1: Cho ABC vuong tại A, đường cao AH. Tính các tỉ số lượng giác của các góc B từ đó suy 
ra các tỉ số lượng giác của góc C, nếu biết:
 a) AB = 16cm; BC = 12 cm b) AB = 13 cm; BH = 5 cm
 c) BH = 16 cm; CH = 9 cm d) AB = 6 cm; AC = 8 cm
HD:
 a) AB = 16cm; AC = 12 cm
 BC AB2 AC 2 122 162 20 cm
 AC 12 3 3 AB 16 4 4
 SinB CosC = ; CosB SinC = 
 BC 20 5 5 BC 20 5 5
 AC 12 3 3 AB 16 4 4
 TanB CotC = CotB TanC = 
 AB 16 4 4 AC 12 3 3
 b) AB = 13 cm; BH = 5 cm
 AH AB2 BH 2 132 52 12 cm
 AH 12 12 BH 5 5
 SinB CosC = ; CosB SinC = 
 AB 13 13 AB 13 13 AH 12 12 BH 5 5
 TanB CotC = CotB TanC = 
 BH 5 5 AH 12 12
 c) BH = 16 cm; CH = 9 cm
 AH BH.CH 16.9 12 cm
 AB AH 2 BH 2 122 162 20 cm
 AH 12 3 3 BH 16 4 4
 SinB CosC = ; CosB = SinC = 
 AB 20 5 5 AB 20 5 5
 AH 12 3 3 BH 16 4 4
 TanB = CotC = CotB = TanC = 
 BH 16 4 4 AH 12 3 3
 d) AB = 6 cm; AC = 8 cm
 BC AB2 AC 2 62 82 10 cm
 AC 8 4 4 AB 6 3 3
 SinB CosC = ; CosB SinC = 
 BC 10 5 5 BC 10 5 5
 AC 8 4 4 AB 6 3 3
 TanB CotC = CotB TanC = 
 AB 6 3 3 AC 8 4 4
Bài 2:Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác của 
góc B Từ đó suy ra tỉ số lượng giác của góc A
HD:
 A
 0,9
 C 1,2 B
 3 4 3 4
 - SinB - cos B - tan B - CotB 
 5 5 4 3
 4 3 4 3
 SinA ; CosA ; tan A ; cot A 
 5 5 3 4
Bài 3:Cho tam giác ABC vuông tại A có AB = 1,6cm, AC = 1,2cm. Tính các tỉ số lượng giác của 
góc B Từ đó suy ra tỉ số lượng giác của góc C
HD: C
 1,2
 A 1,6 B
 3 4 3 4
 - SinB - cos B - tan B - CotB 
 5 5 4 3
 4 3 4 3
 SinC ;CosC ;tanC ;cotC 
 5 5 3 4
Bài 4: Cho tam giác ABC vuông tại A, đường cao AH ( H thuộc BC ), hãy tính sinB và sinC làm 
tròn kết quả đến chữ số thập phân thứ tư trong các trường hợp sau
 a. AB = 13m, BH = 0,5dm b. BH = 3cm, CH = 4cm
HD:
 A
 13
 4 3
 C H 5 B
 a. A/d các tỉ số lượng giác cho tam giác vuông ABH để tính SinB, rồi từ đó suy ra Sin C
 b. Áp dụng hệ thức lượng về cạnh góc vuông và hình chiếu lên cạnh huyền trong tam giác 
vuông ABC để tính AB. Sau đó làm tương tự câu a
Bài 5: Cho ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC, biết: 
 a) AB = 13cm, BH = 5cm. b) BH = 3cm, CH = 4cm.
 HD:
 A
 B C
 H
 2 2 2
 a) Xét ABH vuông tại H có AB AH BH AH 12cm AH 12 BH 5 5
 sin B cos B sin C 
 AB 13 AB 13 13
 A
 B C
 H
 b) Xét ABC vuông tại A có: BC BH HC 3 4 7cm
 AB2 BH.BC 3.7 21 AB 21cm
 AC 2 CH.BC 4.7 28 AC 2 7cm
 AC 2 7 AB 21
 sin B ;sinC 
 BC 7 BC 7
Bài 6: Tính giá trị của x (làm tròn đến chữ số thập phân thứ 3) trong mỗi trường hợp sau. Biết tanB 
 1,072; cosE 0,188. 
HD:
 AC AC 63
 a) Xét ABC vuôngtại A có: tan B AB 58,769
 AB tan B 1,072
 b) Xét DEF vuôngtại D có: ED EF.cosE 16.0,188 3,008cm
 5
Bài 7: Cho tam giác ABC vuông tại A, AB = 6cm, tanB = . Hãy tính độ dài đường cao AH và 
 12
trung tuyến BM của tam giác ABC 
HD:
 A
 M 6
 C H B
 30 601
 Xét ABH (Hˆ 900 ) AH (cm); BM (cm)
 13 4
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH ( H thuộc BC ), biết BH = 4cm, CH = 1cm. 
Hãy giải tam giác ABC HD:
 A
 1 4
 C H B
 Xét tam giác ABC vuông tại A, áp dụng hệ thức lượng trong tam giác vuông, ta có:
 +) AB2 BC.BH AB2 20 AB 2 5(cm) AC 5(cm)
 AC 5 1 AB 
 +) Ta có: tan B B 450 ;tan C 2 C 450
 AB 2 5 2 AC
Bài 9: Cho tam giác ABC vuông tại A, đường cao AH ( H thuộc BC ), biết BH = 4cm, AC = 3 13
cm. Hãy giải tam giác ABC
HD:
 A
 3 13
 4
 C H B
 Đặt HC = x (cm)
 Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:
 2 2 2 x 9(tm)
 AC BC.CH (4 x).x x 4x 9.13 x 4x 4 121 
 x 13(loai)
 Ta có: BC = BH + HC = 13 (cm)
 +) AB2 BH.BC 13.4 52 AB 2 13(cm) 
 AC 3 13 3 
 +) SinB B 560 C 340
 BC 13 13
Bài 10: Cho tam giác ABC vuông tại A, có: AB = 10cm, AC = 15cm
 a. Tính góc B
 b. Phân giác trong của góc B cắt AC tại I. Tính AI
 c. Vẽ AH vuông góc với BI tại H. Tính AH HD:
 B
 10
 H
 A
 I 15 C
 a. Xét tam giác ABC vuông tại A, áp dụng hệ thức lượng trong tam giác vuông, ta có:
 AC 15 3 
 tan B B 560
 AB 10 2
 AI 
 b. Ta có: tan ABI AI AB.t anABI=10.tan280 5,3(cm)
 AB
 AH
 c. SinABH AH AB.sin 280 4,7(cm)
 AB
 2
Bài 11: Cho tam giác ABC vuông tại A, đường cao AH = 6cm( H thuộc BC ), biết tan C cm. 
 3
Hãy tính độ dài các cạnh: HB, HC, AB, AC.
HD:
 B
 H
 6
 A
 C
 2 AH 2
 Theo giả thiết ta có: tan C 
 3 CH 3
 AH HB AB 2 HA.2 6.2 AH.3
 Lại có: AHB : CHA(g.g) HB 4;CH 9
 CH HA AC 3 3 3 2
 Xét tam giác ABC vuông tại A, áp dụng hệ thức lượng trong tam giác vuông ta có:
 AB2 BH.HC AB 2 13(cm); AC 2 CH.CB AC 3 13(cm)
Bài 12: Cho ABC vuông tại C, trong đó AC = 0,90m, BC = 1,20m. Tính các tỉ số lượng giác của 
góc B, từ đó suy ra các tỉ số lượng giác của góc A.
 HD: A
 0,9
 α
 B
 1,2 C
 AB BC 2 AC 2 1,5 cm
 AC 0,9 3 3 BC 1,2 4 4
 SinB CosA = ; CosB SinA = 
 AB 1,5 5 5 AB 1,5 5 5
 AC 0,9 3 3 BC 1,2 4 4
 TanB CotA = CotB TanA = 
 AB 1,2 4 4 AC 0,9 3 3
Bài 13: Cho hình bên:
 3
 Biết tan . Hãy tính:
 4
 a) Cạnh AC. 
 b) Cạnh BC.
HD:
 3 AC 3 3 3
 tan AC .AB .6 4,5 cm
 4 AB 4 4 4
 BC AB2 AC 2 62 4,52 7,5 cm
 µ 0
Bài 14: Cho ABC vuông tại A, B 30 , BC = 8cm. Hãy tính cạnh AB (làm tròn đến chữ số thập 
phân thứ ba). Biết cos300 0,866. 
HD:
 C
 8 cm
 30°
 B
 A
 AB
 cosB AB BC.cosB 8.cos30 4 3
 BC Bài 15: Cạnh huyền của một tam giác vuông có một góc bằng 600 là 8. Hãy tìm độ dài của cạnh đối 
diện với góc 600.
HD:
 A
 600
 C
 B 8
 Xét ABC vuôngtại A có : AC BC.sinB 8.sin 600 4 3
Bài 16: Cạnh góc vuông kề với góc 60 0 của một tam giác vuông bằng 3. Hãy tìm cạnh huyền và 
cạnh góc vuông còn lại (sử dụng bảng lượng giác của các góc đặc biệt). 
HD:
 A
 3
 600
 B C
 Xét ABC vuông tại A có : AC AB.tan B 3.tan 600 3 3
 AB AB 3
 cosB BC 6
 BC cos B cos600
Bài 17:Cho tam giác ABC có AB a 5, BC a 3, AC a 2
 a) Chứng minh tam giác ABC vuông
 b) Tính các tỉ số lượng giác của góc B Từ đó suy ra các tỉ số lượng giác của góc A
HD: A
 C B
 a) Dùng định lý pytago đảo, ta có: 
 AB2 AC 2 BC 2 5a2 3a2 2a2 ABC vuông tại C 2 6 3 15
 b) - SinB - cos B 
 5 5 5 5
 2 6 3 3 6
 - tan B - CotB 
 3 3 6 6
 5
Bài 18:Cho t/giác ABC vuông tại A, AB = 5cm, cot B . Tính độ dài các đoạn thẳng AC và BC 
 8
 a) Chứng minh tam giác ABC vuông
 b) Tính các tỉ số lượng giác của góc B Từ đó suy ra các tỉ số lượng giác của góc A
HD:
 Áp dụng tỉ số CotB trong tam giác vuông ABC và định lý pytago ta tính được 
 AC 8cm, BC 89cm
Bài 19: Cho MNP vuông ở M, đường cao MQ chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 
6. Hãy so sánh cotN và cotP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần.
HD:
 M
 P
 N Q
 NQ
 Xét MNQ vuôngtạiQ có cot N 
 MQ
 PQ
 Xét MPQ vuôngtạiQ có cotP 
 MQ
 cot N NQ PQ NQ 1
 : cot P 2cot N
 cot P MQ MQ PQ 2
Bài 20: Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.
 a) Tính diện tích ABD.
 3 4
 b) Tính AC, dùng các thông tin sau đây nếu cần: sin , cosC .
 5 5
HD: