Đề thi giải toán trên máy tính cầm tay cấp huyện Lớp 9 - Năm học 2012-2013

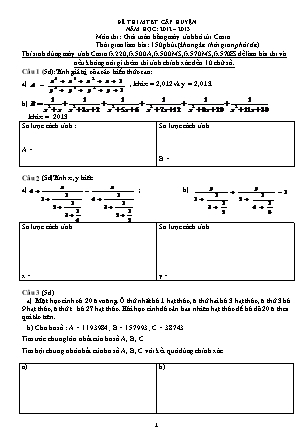
ĐỀ THI MTBT CẤP HUYỆN 
 NĂM HỌC: 2012 – 2013
Môn thi: Giải toán bằng máy tính bỏ túi Casio .
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Thí sinh dùng máy tính Casio fx220, fx500A,fx500MS,fx570MS,fx570ES để làm bài thi và nếu không nói gì thêm thì tính chính xác đến 10 chữ số.
Câu 1 (5đ):TÝnh gi¸ trÞ cña c¸c biÓu thøc sau:
a) , khi x = 2,012 vµ y = 2,013.
b) 
 khi x = 2013
Sơ lược cách tính :
A = 
Sơ lược cách tính 
B = 
Câu 2 (5đ)TÝnh x, y biÕt: 
a) ; b) 
Sơ lược cách tính
x = 
Sơ lược cách tính 
y = 
Câu 3 (5đ)
 a) Mét häc sinh cã 20 « vu«ng. ¤ thø nhÊt bá 1 h¹t thãc, « thø hai bá 3 h¹t thãc, « thø 3 bá 9 h¹t thãc, « thø t­ bá 27 h¹t thãc. Hái häc sinh ®ã cÇn bao nhiªu h¹t thãc ®Ó bá ®ñ 20 « theo qui t¾c trªn.
 b) Cho ba số : A = 1193984 ; B = 157993 ; C = 38743
Tìm ước chung lớn nhất của ba số A, B, C.
Tìm bội chung nhỏ nhất của ba số A, B, C với kết quả đúng chính xác.
a)
b)
Bài 4: (5 điểm)
 Một người gửi tiết kiệm 100 000 000 đồng (tiền Việt Nam) vào một ngân hàng theo mức kỳ hạn 12 tháng với lãi suất 0,75% một tháng.
 a) Hỏi sau 5 năm, người đó nhận được bao nhiêu tiền (cả vốn và lãi) ở ngân hàng. Biết rằng người đó không rút lãi ở tất cả các định kỳ trước đó.
 b) Nếu với số tiền trên, người đó gửi tiết kiệm theo mức kỳ hạn 6 tháng với lãi suất 11% năm thì sau 10 năm sẽ nhận được bao nhiêu tiền (cả vốn và lãi) ở ngân hàng. Biết rằng người đó không rút lãi ở tất cả các định kỳ trước đó.
(Kết quả lấy theo các chữ số trên máy khi tính toán.
Theo kỳ hạn 12 tháng
Theo kỳ hạn 6 tháng 
Bài 5: (5 điểm)
a) Tìm cặp số (x;y) nguyên dương sao cho
b) Tìm lớn nhất và nhỏ nhất trong các số tự nhiên dạng mà chia hết cho 5, 7 và 9
Kết quả:
a) ( ; )
b) Số lớn nhất:
 Số nhỏ nhất:
Bài 6 : (5 điểm)
1) Giải phương trình sau , tính x theo a, b (với a > 0, b > 0) 
2) Cho biết a = 250204 ; b = 260204
 Sơ lược cách giải
Nghiệm x = 
Câu 7: (5đ) Cho h×nh thang vu«ng ABCD cã AB = 12,35cm ; BC = 10,55cm
C¸c gãc: TÝnh:
Hình vẽ: 
Chu vi hình thang vuông ABCD
DiÖn tÝch h×nh thang vu«ng ABCD.
Số đo c¸c gãc cßn l¹i cña tam gi¸c ADC (®é, phót)
Bài 8: (5 điểm)
1)Cho M = 0,1(23) + 0,6(92)
Giá trị M (ghi ở dạng phân số) = 
2) Số thập phân tuần hoàn A= 3,5(23) được sinh ra bởi phân số nào ?
A=
3) Chữ số đứng ở vị trí thứ 2012 ở phần thập phân trong kết quả của phép chia 19 cho 21 là chữ số nào?
Chu kỳ tuần hoàn có : .... chữ số 
chữ số thứ 2012 phần thập phân là số: .........
4) Tìm thương và dư trong phép chia đa thức :
x7 – 2x5 – 3x4 + x – 1 cho x + 5 
Thương:
Dư: ..
Bài 9 : (5 điểm) Tam giác ABC vẽ đường cao AH và có các cạnh AB = 6 dm, 
 góc A = 103o31’, góc C = 35o40’ 
Tính gần đúng diện tích tam giác
S =
Tính đường cao AH.
AH = 
Bài 10 : (5 điểm) Trong mặt phẳng tọa độ cho ba điểm A(-2 ; 5), B(-4 ; 2), C(7 ; -1). Từ đỉnh A vẽ đường cao AH, đường phân giác AD và đường trung tuyến AM (các điểm H, D, M thuộc cạnh BC).
a) Tính diện tích tam giác ABC. Nêu sơ lược cách giải
b) Tính độ dài của AH, AD, AM và diện tích tam giác ADM
(kết quả lấy với 2 chữ số ở phần thập phân). Đơn vị đo trên các trục tọa độ là cm.
Hình vẽ 
a) Sơ lược cách giải : 
SABC = .....................
AH = .....................
AM = .....................
AD = ......................
SADM = .....................
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM