Chuyên đề Hình học Lớp 12 - Chương 3: Phương pháp tọa độ trong không gian Oxyz - Bài 1: Hệ tọa độ trong không gian

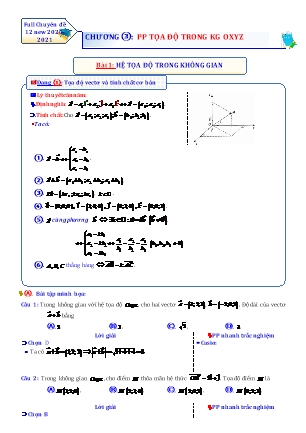
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ③: PP TỌA ĐỘ TRONG KG OXYZ
 Bài 1: HỆ TỌA ĐỘ TRONG KHÔNG GIAN 
  Dạng ①: Tọa độ vectơ và tính chất cơ bản
 . Lý thuyết cần nắm:
 .Định nghĩa: a a1.i a2. j a3.k a a 1 ;a2 ;a3 .
 .Tính chất: Cho a a 1 ;a2 ;a3 ;b b1 ;b2 ;b3 . 
 Ta có:
 a1 b1
 ①. .a b a2 b2
 a3 b3
 ②. .a b a 1 b1 ;a2 b2 ;a3 b3 
 ③. ka ka 1 ;ka2 ;ka3 , k ¡ .
 ④. .0 (0;0;0), i 1;0;0 , j 0;1;0 , k 0;0;1 
 ⑤. acùng phương b k ¡ : a kb b . 0 
 a1 kb1
 a1 a2 a3
 a2 kb2 b1,b2 ,b3 0 
 b1 b2 b3
 a3 kb3
   
 ⑥. thẳngA, B,C hàng. AB k.AC
Ⓐ. Bài tập minh họa:
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a 3;2;1 , b 2;0;1 . Độ dài của vectơ 
 a b bằng
 Ⓐ. 2 . Ⓑ.1 . Ⓒ. 2 . Ⓓ. 3.
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio: 
  Ta có a b 1;2;2 a b 1 4 4 3.
  
Câu 2: Trong không gian Oxyz , cho điểm M thỏa mãn hệ thức OM 2i j . Tọa độ điểm M là
 Ⓐ. M 1;2;0 . Ⓑ. M 2;1;0 . Ⓒ. M 2;0;1 . Ⓓ. M 0;2;1 .
 Lời giải PP nhanh trắc nghiệm
 Chọn B
  Ta sử dụng định nghĩa, nếu điểm M thỏa mãn:  Hệ số trước i, j,k .
 OM xi y j zk thì M x; y; z với i, j,k lần lượt là các véc tơ  Suy ra M x; y; z 
đơn vị trên các trục Ox,Oy,Oz .
  
Câu 3: Trong không gian Oxyz , cho hai điểm A 1;1;3 , B 2;5;4 . Vectơ AB có tọa độ là
 Ⓐ. 3;6;7 . Ⓑ. 1; 4; 1 . Ⓒ. 3; 6;1 . Ⓓ. 1;4;1 .
 Lời giải PP nhanh trắc nghiệm
  
 Chọn D 
  Ta có AB 1;4;1 
Ⓑ.Bài tập rèn luyện:
Câu 1: Trong không gian Oxyz , cho các vectơ a 1; 1;2 , b 3;0; 1 và c 2;5;1 . Tọa độ của 
 vectơ u a b c là
 Ⓐ.u 0;6; 6 . Ⓑ.u 6;0; 6 . Ⓒ. u 6; 6;0 . Ⓓ. u 6;6;0 .
Câu 2: Trong không gian với hệ trục tọa độ Oxyz , cho a 2; 3;3 , b 0; 2; 1 , c 3; 1;5 . Tìm 
 tọa độ của vectơ u 2a 3b 2c .
 Ⓐ. 10; 2;13 . Ⓑ. 2;2; 7 . Ⓒ. 2; 2;7 . Ⓓ. 2;2;7 .
Câu 3: Trong mặt phẳng với hệ tọa độ Oxyz, cho véc tơ a = (2;- 2;- 4),b = (1;- 1;1). Mệnh đề nào 
 dưới đây là mệnh đề sai?
 Ⓐ. a + b = (3;- 3;- 3). Ⓑ. a và b cùng phương.
 Ⓒ. b = 3. Ⓓ. a ^ b..
  
Câu 4: Trong không gian tọa độ Oxyz , cho điểm M a;b;c . Tọa độ của véc-tơ MO là
 Ⓐ. a;b;c . Ⓑ. a;b;c .
 Ⓒ. a; b; c . Ⓓ. a;b; c .
Câu 5: Trong không gian Oxyz , cho a 1;2; 3 , b 2; 4;6 . Khẳng định nào sau đây là đúng?
 Ⓐ. a 2b. Ⓑ.b 2a . Ⓒ. a 2b . Ⓓ. b 2a.
Câu 6: Trong không gian với trục hệ tọa độ Oxyz , cho a i 2 j 3k. Tọa độ của vectơ a là
 Ⓐ. a 1;2; 3 . Ⓑ. a 2; 3; 1 . Ⓒ. a 3;2; 1 . Ⓓ. a 2; 1; 3 .
Câu 7: Trong không gian tọa độ Oxyz , độ dài của véc tơ u (1;2;2) là
 Ⓐ.3. Ⓑ.5. Ⓒ. 2. Ⓓ. 9.
 uuur
Câu 8: Trong không gian Oxyz , cho hai điểm A 1;1; 1 , B 2;3; 2 . Vectơ AB có tọa độ là
 Ⓐ. 1;2;3 . Ⓑ. 1; 2;3 . Ⓒ. 3;5;1 . Ⓓ. 3;4;1 .
Câu 9: Trong không gian với trục hệ tọa độ Oxyz , cho a i 2 j 3k. Tọa độ của vectơ a là
 Ⓐ. a 1;2; 3 . Ⓑ. a 2; 3; 1 . Ⓒ. a 3;2; 1 . Ⓓ. a 2; 1; 3 . Câu 10: Trong mặt phẳng Oxy , cho A m 1;2 , B 2;5 2m và C m 3;4 . Tìm giá trị m để A , B , 
 C thẳng hàng?
 Ⓐ. m 2. Ⓑ. m 2 . Ⓒ. m 1. Ⓓ. m 3.
Câu 11: Trong không gian với hệ tọa độ Oxyz , để hai véctơ a = (m;2;3) và b = (1;n;2) cùng phương 
 thì m + n bằng
 11 13 17
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 2 .
 6 6 6
Câu 12: Trong không gian với hệ trục tọa độ Oxyz , cho u = (1;1;2), v = (- 1;m;m- 2). Khi đó 
 éu,vù= 14 thì
 ëê ûú
 11 11
 Ⓐ. m = 1,m = - . Ⓑ. m = - 1,m = - .
 5 3
 Ⓒ. m = 1,m = - 3. Ⓓ. m= - 1.
Câu 13: Trong không gian với hệ trục tọa độ Oxyz , cho 2 điểm B(1;2;- 3) và C(7;4;- 2). Nếu điểm E 
   
 thỏa mãn đẳng thức CE = 2EB thì tọa độ điểm E là
 æ 8 8ö æ8 8ö æ 8ö æ 1ö
 Ⓐ.ç3; ;- ÷. Ⓑ.ç ;3;- ÷. Ⓒ. ç3;3;- ÷ Ⓓ. ç1;2; ÷
 èç 3 3ø÷ èç3 3ø÷ èç 3ø÷ èç 3ø÷
Câu 14: Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(2;- 1;5), B(5;- 5;7), M(x; y;1). Với giá 
 trị nào của x , y thì A , B , M thẳng hàng?
 Ⓐ. x = 4 ; y = 7 . Ⓑ. x = - 4; y = - 7 . Ⓒ. x = 4 ; y = - 7 . Ⓓ. x = - 4; y = 7 .
Câu 15: Trong không gian với hệ tọa độ Oxyz cho hình bình hành ABCE với A 3;1;2 , B 1;0;1 ,
 C 2;3;0 . Tọa độ đỉnh E là
 Ⓐ. E 4;4;1 . Ⓑ. E 0;2; 1 . Ⓒ. E 1;1;2 . Ⓓ. E 1;3; 1 .
Câu 16: Trong không gian với hệ tọa độ Oxyz , cho A(1; 2;0), B(1;0; 1), C(0; 1;2), D( 2;m;n). Trong 
 các hệ thức liên hệ giữa m, n dưới đây, hệ thức nào để bốn điểm A, B, C, D đồng phẳng?
 Ⓐ. 2m n 13. Ⓑ. 2m n 13. Ⓒ. m 2n 13. Ⓓ. 2m 3n 10.
 BẢNG ĐÁP ÁN
 1.C 2.B 3.B 4.C 5.B 6.A 7.A 8.A 9.A 10.B
 11.B 12.C 13.A 14.D 15.A 16.C  Dạng ②: Tọa độ điểm
 
 . Lý thuyết cần nắm:  
 Ⓐ. Định nghĩa: M (x; y; z) OM x.i y. j z.k (x : hoành độ, y : tung độ, z : cao độ)
 Ⓑ. Chú ý: 
 ①. M Oxy z 0;M Oyz x 0;M Oxz y 0
 ②. .M Ox y z 0;M Oy x z 0;M Oz x y 0
 Ⓒ. Tính chất: Cho A(x ; y ; z ), B(x ; y ; z )
  A A A B B B
 ①. AB (xB xA; yB yA; zB zA )
 2 2 2
 ②. AB (xB xA ) (yB yA ) (zB zA )
 x x y y z z 
 ③. Toạ độ trung điểm M của đoạn thẳng AB : M A B ; A B ; A B 
 2 2 2 
 ④. Toạ độ trọng tâm G của tam giác ABC : 
 x x x y y y z z z 
 G A B C ; A B C ; A B C 
 3 3 3 
 . 
Ⓐ - Bài tập minh họa: 
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho A 1;3;2 , B 3; 1;4 . Tìm tọa độ trung điểm I của 
 AB.
 Ⓐ. I 2; 4;2 . Ⓑ. I 4;2;6 . Ⓒ. I 2; 1; 3 . Ⓓ. I 2;1;3 .
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Tổng chia đôi
 xA xB
 xI 2
 2
 yA yB
  Ta có yI 1 I 2;1;3 .
 2
 zA zB
 zI 3
 2
Câu 2: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A 1;3;5 , B 2;0;1 , C 0;9;0 . Tọa độ trọng 
 tâm G của tam giác ABC là
 Ⓐ.G 1;5;2 . Ⓑ.G 1;0;5 . Ⓒ. G 3;12;6 . Ⓓ. G 1;4;2 .
 Lời giải PP nhanh trắc nghiệm
  Chọn D  Tổng chia ba
  Ta có G x; y; z là trọng tâm tam giác ABC nên 
 1 2 0
 x 1
 3
 3 0 9
 y 4 G 1;4;2 .
 3
 5 1 0
 z 2
 3
Câu 3: Trong không gian Oxyz cho điểm A 1; 2;3 . Hình chiếu vuông góc của điểm A trên mặt phẳng 
 Oyz là điểm M . Tọa độ điểm M là
 Ⓐ. M 1;0;3 . Ⓑ. M 0; 2;3 . Ⓒ. M 1;0;0 . Ⓓ. M 1; 2;0 . Lời giải PP nhanh trắc nghiệm
 Chọn C  “Chiếu lên mặt nào có thành 
 Phương trình mặt phẳng Oyz : x 0. phần mặt đó, còn lại bằng 0” 
Phương trình tham số của đường thẳng d đi qua A và vuông M 0; 2;3 
 x 1 t
góc với mặt phẳng Oyz là: y 2 .
 z 3
Do đó M d  Oyz M 0; 2;3 . 
Ⓑ- Bài tập rèn luyện:
Câu 1: Trong không gian Oxyz cho hai điểm A 1;2;3 , B 1;0;1 . Trọng tâm G của tam giác OAB 
 có tọa độ là
 2 4 
 Ⓐ. 0;1;1 . Ⓑ. 0; ; . Ⓒ. 0;2;4 . Ⓓ. 2; 2; 2 .
 3 3 
Câu 2: Trong không gian với hệ trục tọa độ Oxyz , cho tam giác ABC có ba đỉnh A a;0;0 , B 0;b;0 , 
 C 0;0;c . Tọa độ trọng tâm của tam giác ABC là
 Ⓐ. a;b;c . Ⓑ. a; b; c .
 a b c a b c 
 Ⓒ. ; ; . Ⓓ. ; ; .
 3 3 3 3 3 3 
Câu 3: Trong không gian Oxyz cho điểm A 2;1;3 . Hình chiếu vuông góc của A lên trục Ox có tọa 
 độ là:
 Ⓐ. 0;1;0 . Ⓑ. 2;0;0 . Ⓒ. 0;0;3 . Ⓓ. 0;1;3 .
Câu 4: Trong không gian với hệ tọa độ Oxyz , hình chiếu vuông góc của điểm A 3;2; 4 lên mặt 
 phẳng Oxy có tọa độ là
 Ⓐ. 0;2; 4 . Ⓑ. 0;0; 4 . Ⓒ. 3;0; 4 . Ⓓ. 3;2;0 .
Câu 5: Trong không gian với hệ trục tọa độ Oxyz , cho A 0; 1;1 , B 2;1; 1 , C 1; 3; 2 . Biết rằng 
 ABCD là hình bình hành, khi đó tọa độ điểm D là
 2 
 Ⓐ. D 1;1; 4 . Ⓑ. D 1;1; . Ⓒ. D 1; 3; 4 . Ⓓ. D 1; 3; 2 
 3 
Câu 6: Trong không gian tọa độ Oxyz , cho điểm A(3; 2;5) . Hình chiếu vuông góc của điểm A trên 
 mặt phẳng tọa độ (Oxz) :
 Ⓐ. M (3; 2;0) . Ⓑ. M (3;0;5) . Ⓒ. M (0; 2;5) . Ⓓ. M (0;2;5) .
Câu 7: Trong không gian Oxyz , cho 2 điểm M 1; 2;2 và N 1;0; 4 . Toạ độ trung điểm của đoạn 
 thẳng MN là:
 Ⓐ. 1; 1;3 . Ⓑ. 0;2;2 . Ⓒ. 2; 2;6 . Ⓓ. 1;0;3 .
Câu 8: Trong không gian Oxyz , cho điểm M 1; 2;5 . Khoảng cách từ M đến trục Oz bằng
 Ⓐ. 5 . Ⓑ.5. Ⓒ. 1. Ⓓ. 2 .
Câu 9: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A 3;2; 1 , B 1;0;5 . Tọa độ trung điểm 
 I của đoạn thẳng AB là Ⓐ. I 2;1; 3 . Ⓑ. I 1;1;2 . Ⓒ. I 2; 1;3 . Ⓓ. I 4; 2;6 .
Câu 10: Trong không gian cho hai điểm A 1;2;3 , B 0;1;1 độ dài đoạn AB bằng
 Ⓐ. 6 . Ⓑ. 8 . Ⓒ. 10 . Ⓓ. 12 .
Câu 11: Trong không gian Oxyz , cho ba điểm A 1;0; 2 , B 2;1; 1 ,C 1; 2;2 . Tìm tọa độ trọng tâm 
 G của tam giác ABC .
 3 1 3 4 1 1 
 Ⓐ.G ; ; . Ⓑ.G ; ; . Ⓒ. G 1; 1;0 . Ⓓ. G 4; 1; 1 .
 2 2 2 3 3 3 
Câu 12: Trong không gian Oxyz, cho hai điểm A(1; 1;2) ; B(2;1;1) . Độ dài đoạn AB bằng:
 Ⓐ.2. Ⓑ. 6 . Ⓒ. 2 . Ⓓ. 6.
Câu 13: Trong không gian Oxyz , cho điểm M (1;2;3) . Tọa độ điểm M ¢ đối xứng với M qua mặt phẳng 
 (Oxy) là
 Ⓐ..( - 1;- 2;3)Ⓑ.. Ⓒ.(1 .; - 2;- 3) Ⓓ. . (1;2;- 3) (- 1;2;- 3)
Câu 14: Trong không gian Oxyz , cho hai điểm A 3;0;2 và B 2;1;1 . Đoạn AB có độ dài là
 Ⓐ.3 3 . Ⓑ.3. Ⓒ. 3 . Ⓓ. 2 .
Câu 15: Trong không gian với hệ tọa độ Oxyz , cho ba điểm M 1;1;1 , N 2;3;4 , P 7;7;5 . Để tứ giác 
 MNPQ là hình bình hành thì tọa độ điểm Q là
 Ⓐ. 6; 5; 2 . Ⓑ. 6; 5;2 . Ⓒ. 6;5;2 . Ⓓ. 6;5;2 .
Câu 16: Cho tam giác ABC có A 1; 2;0 , B 2;1; 2 , C 0;3;4 . Tìm tọa độ điểm D để tứ giác ABCD 
 là hình bình hành.
 Ⓐ. D 1;0; 6 . Ⓑ. D 1;6; 2 . Ⓒ. D 1;0;6 . Ⓓ. D 1;6; 2 .
Câu 17: Trong không gian Oxyz , cho hai điểm B(0;3;1) , C(- 3;6;4) . Gọi M là điểm nằm trên đoạn 
 BC sao cho MC = 2MB . Tính tọa độ điểm M .
 Ⓐ. M (- 1;4;- 2) . Ⓑ. M (- 1;4;2) . Ⓒ. M (1;- 4;- 2) . Ⓓ. M (- 1;- 4;2) .
Câu 18: Trong mặt phẳng Oxy , cho A m 1;2 , B 2;5 2m và C m 3;4 . Tìm giá trị m để A , B , 
 C thẳng hàng?
 Ⓐ. m 2. Ⓑ. m 2 . Ⓒ. m 1. Ⓓ. m 3.
Câu 19: Trong không gian với hệ tọa độ Oxyz . Tam giác ABC với A(1;- 3;3),B(2;- 4;5),C(a;- 2;b) 
 nhận điểm G(2;c;3) làm trọng tâm của nó thì giá trị của tổng a + b + c bằng
 Ⓐ.- 5 . Ⓑ.3 . Ⓒ. 1. Ⓓ. - 1.
Câu 20: Trong không gian với hệ tọa độ Oxyz cho hình bình hành ABCE với A 3;1;2 , B 1;0;1 ,
 C 2;3;0 . Tọa độ đỉnh E là
 Ⓐ. E 4;4;1 . Ⓑ. E 0;2; 1 . Ⓒ. E 1;1;2 . Ⓓ. E 1;3; 1 .
 BẢNG ĐÁP ÁN
 1.B 2.C 3.B 4.D 5.A 6.B 7.A 8.A 9.B 10.A
 11.B 12.B 13.C 14.C 15.C 16.C 17.B 18.B 19.C 20.A  Dạng ③: Tích vô hướng và ứng dụng
 . Lý thuyết cần nắm:
 Ⓐ. Định nghĩa: Trong không gian Oxyz cho hai vectơ a (a ;a ;a ) , b (b ;b ;b ) . 
 1 2 3 1 2 3
 . Tích vô hướng của hai véc tơ : a.b a . b .cos a,b a1b1 a2b2 a3b3
 . Tích có hướng của hai vectơ a và b, kí hiệu là a,b , được xác định bởi
 a2 a3 a3 a1 a1 a2 
 a,b ; ; a2b3 a3b2 ;a3b1 a1b3;a1b2 a2b1 
 b2 b3 b3 b1 b1 b2 
 Ⓑ. Chú ý: Tích có hướng của 2 vectơ là 1 vectơ, tích vô hướng của 2 vectơ là 1 số.
 Ⓒ. Tính chất: 
 . [a, b]  a; [a, b]  b . a, b b,a 
 . i , j k ; j, k i ; k , i j . [a,b] a . b .sin a,b 
 . a, b cùng phương [a, b] 0. .a, b, c đồng phẳng [a, b].c 0
 Ⓓ. Ứng dụng của tích có hướng:
 . Điều kiện đồng phẳng của ba vectơ: a, b và c đồng phẳng [a, b].c 0
   
 . Diện tích hình bình hành ABCD : SY ABCD AB, AD 
 1   
 . Diện tích tam giác ABC : S ABC AB, AC 
 2
    
 . Thể tích khối hộp ABCDA B C D : VABCD.A'B'C 'D' [AB, AD].AA 
 1    
 . Thể tích tứ diện:ABCD V [AB, AC].AD
 ABCD 6
 a.b a b a b a b
 . Góc giữa hai véc tơ: cos a;b 1 1 2 2 3 3
 2 2 2 2 2 2
 a . b a1 a2 a3 . b1 b2 b3
Ⓐ. Bài tập minh họa:
Câu 1: Trong không gian với hệ tọa độ Oxyz , cho ba điểm M 2;3; 1 , N 1;1;1 , P 1;m 1;3 . Với 
 giá trị nào của m thì tam giác MNP vuông tại N
 Ⓐ. m 3 . Ⓑ. m 1. Ⓒ. m 2 . Ⓓ. m 0 .
 Lời giải PP nhanh trắc nghiệm
  Chọn  B   Casio: Solve
  Ta có NM 3;2; 2 , NP 2;m 2;2 
   
  Tam giác MNP vuông tại N khi NM.NP 0
 2.3 2(m 2) 4 0 m 1.
Câu 2: Trong không gian, với hệ tọa độ Oxyz , cho tứ diện ABCD có A(2;- 1;1), B(3;0;- 1), C(2;- 1;3), 
 D Î Oy và có thể tích bằng 5 . Tính tổng tung độ của các điểm D .
 Ⓐ.- 6 . Ⓑ. 2 . Ⓒ. 7 . Ⓓ. - 4 .
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Casio:
 Do D Î Oy Þ D(0;m;0).
    
 AB = (1;1;- 2), AC = (0;0;2), AD = (- 2;m + 1;- 1).
 1    1
Ta có: V = 5 Þ éAB, ACù.AD = 5 Þ - 6- 2m = 5
 ABCD 6 ëê ûú 6
 ém = 12
 Û ê .
 ëêm = - 18
Vậy tổng tung độ của các điểm D là 12+ (- 18)= - 6.
Câu 3: Trong không gian tọa độ Oxyz góc giữa hai vectơ i và u 3;0;1 là
 Ⓐ.120 . Ⓑ.30 . Ⓒ. 60 . Ⓓ. 150 .
 Lời giải
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio
 Ta có i 1;0;0 
 u.i 3 
 cos u,i . Vậy u,i 150 .
 u . i 2
Ⓑ. Bài tập rèn luyện:
  
Câu 1: Trong không gian Oxyz cho hai điểm A 2;3;4 và B 3;0;1 . Khi đó độ dài vectơ AB là
 Ⓐ. 19 . Ⓑ.19. Ⓒ. 13 . Ⓓ. 13.
Câu 2: Trong không gian Oxyz , cho hai điểm A( 2;1; 3) và B(1;0; 2) . Độ dài đoạn thẳng AB bằng
 Ⓐ.3 3 . Ⓑ.11. Ⓒ. 11. Ⓓ. 27.
Câu 3: Trong không gian Oxyz cho a 2;3; 1 ; b 2; 1;3 . Sin của góc giữa a và b bằng
 2 3 5 3 5 2
 Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. .
 7 7 7 7
Câu 4: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A 1;0;1 và B 4;2; 2 . Độ dài đoạn thẳng 
 AB bằng
 Ⓐ. 22 . Ⓑ. 4 . Ⓒ. 2 . Ⓓ. 22 .
Câu 5: Trong không gian tọa độ Oxyz , góc giữa hai vectơ i và u 3;0;1 là
 Ⓐ.300 . Ⓑ.1200 . Ⓒ. 600 . Ⓓ. 1500 .
Câu 6: Trong không gian với hệ trục tọa độ Oxyz , cho A 2;0;0 ; B 0;3;1 ; C 3;6;4 . Gọi M là điểm 
 nằm trên đoạn BC sao cho MC 2MB . Độ dài AM là
 Ⓐ. 29 . Ⓑ.3 3 . Ⓒ. 3 0 . Ⓓ. 2 7 . 
Câu 7: Cho hai vec tơ a 1; 2;3 ,b 2;1;2 . Khi đó tích vô hướng a b .b bằng
 Ⓐ.12 . Ⓑ. 2 . Ⓒ. 11. Ⓓ. 10 .
Câu 8: Trong không gian Oxyz , cho các vectơ a 5; 3; 2 và b m; 1; m 3 . Có bao nhiêu giá trị 
 nguyên dương của m để góc giữa hai vectơ a và b là góc tù?
 Ⓐ. 2 . Ⓑ.3. Ⓒ. 1 . Ⓓ. 5.
Câu 9: Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có A 1;0;0 , B 0;0;1 , C 2;1;1 . Diện 
 tích tam giác ABC bằng:
 11 7 6 5
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 2 2 2 2
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A' B 'C ' D ' có A 0;0;0 , B a;0;0 ,
 D 0;2a;0 , A' 0;0;2a với a 0. Độ dài đoạn thẳng AC ' là
 3 a
 Ⓐ.3 a . Ⓑ. . Ⓒ. 2 a . Ⓓ. a .
 2
  
Câu 11: Trong không gian với hệ tọa độ Oxyz , cho OA 3i j 2k và B m;m 1; 4 . Tìm tất cả giá trị 
 của tham số m để độ dài đoạn AB 3.
 Ⓐ. m 2 hoặc m 3. Ⓑ. m 1 hoặc m 4 .
 Ⓒ. m 1 hoặc m 2 . Ⓓ. m 3 hoặc m 4 .
Câu 12: Trong không gian với hệ tọa độ Oxyz , cho mặt phẳng P :2x 3y z 3 0 . Gọi M , N lần 
 lượt là giao điểm của mặt phẳng P với các trục Ox , Oz . Tính diện tích tam giác OMN .
 9 9 3 3
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 4 2 2 4
Câu 13: Trong không gian với hệ tọa độ Oxyz , cho véc tơ u 1;1; 2 , v 1;0;m . Tìm tất cả giá trị của 
 m để góc giữa u , v bằng 45.
 Ⓐ. m 2 . Ⓑ. m 2 6 . Ⓒ. m 2 6 . Ⓓ. m 2 6 .
Câu 14: Trong không gian tọa độ Oxyz góc giữa hai vectơ i và u 3;0;1 là
 Ⓐ.120 . Ⓑ.30 . Ⓒ. 60 . Ⓓ. 150 .
Câu 15: Cho u 1;1;0 ,v 0; 1;0 , góc giữa hai vectơ u và v là
 Ⓐ.1200 . Ⓑ. 450 . Ⓒ. 1350 . Ⓓ. 600 .
Câu 16: Trong không gian Oxyz cho hai vectơ a (1; 1;2) và b (2;1; 1) . Tính a.b .
 Ⓐ. a.b (2; 1; 2) . Ⓑ. a.b ( 1;5;3) . Ⓒ. a.b 1. Ⓓ. a.b 1.
Câu 17: Trong không gian Oxyz , tích vô hướng của hai vectơ a 3 ; 2 ;1 và b 5 ; 2 ; 4 bằng
 Ⓐ. 15 . Ⓑ. 10 . Ⓒ. 7 . Ⓓ. 15.
Câu 18: Trong không gian Oxyz , cho A 3;0;0 , B 0;0;4 . Chu vi tam giác OAB bằng
 Ⓐ.14 . Ⓑ.7 . Ⓒ. 6 . Ⓓ. 12 . 
Câu 19: Trong không gian hệ tọa độ Oxyz , cho u 1;2; 1 và v 2;3;0 . Tính u,v .
 Ⓐ. u,v 3;2; 1 . Ⓑ. u,v 3; 2;1 .
 Ⓒ. u,v 3; 2; 1 . Ⓓ. u,v 3;2;1 .
Câu 20: Trong không gian Oxyz , cho các vectơ a m;1;0 , b 2;m 1;1 , c 1;m 1;1 . Tìm m để 
 ba vectơ a,b ,c đồng phẳng
 3 1
 Ⓐ. m 2. Ⓑ. m . Ⓒ. m 1. Ⓓ. m .
 2 2
Câu 21: Trong không gian Oxyz cho a 3;4;0 ; b 5;0;12 . Cosin của góc giữa a và b bằng
 3 5 5 3
 Ⓐ.. Ⓑ.. Ⓒ. . Ⓓ. . 
 13 6 6 13
Câu 22: Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a ( 2; 3;1) , b (1;0;1) . Tính cos(a,b) .
 1 1 3 3
 Ⓐ. cos(a,b) . Ⓑ. cos(a,b) . Ⓒ. cos(a,b) . Ⓓ. cos(a,b) .
 2 7 2 7 2 7 2 7
Câu 23: Trong không gian hệ tọa độ Oxyz , cho ba điểm không thẳng hàng A 1;2;4 , B 1;1;4 , 
 C 0;0;4 . Tam giác ABC là tam giác gì?
 Ⓐ.Tam giác tù. Ⓑ.Tam giác vuông. Ⓒ. Tam giác đều. Ⓓ. Tam giác nhọn.
Câu 24: Trong không gian với hệ tọa độ Oxyz cho hai điểm A 1; 1;0 , B 3;1; 1 . Điểm M thuộc 
 trục Oy và cách đều hai điểm A , B có tọa độ là:
 9 9 9 9 
 Ⓐ. M 0; ;0 . Ⓑ. M 0; ;0 . Ⓒ. M 0; ;0 . Ⓓ. M 0; ;0 .
 4 2 2 4 
Câu 25: Trong không gian Oxyz , cho hai điểm A 1;2;0 , B 2; 1;1 . Tìm điểm C có hoành độ dương 
 trên trục Ox sao cho tam giác ABC vuông tại C .
 Ⓐ.C 3;0;0 . Ⓑ.C 2;0;0 . Ⓒ. C 1;0;0 . Ⓓ. C 5;0;0 .
 BẢNG ĐÁP ÁN
 1.A 2.C 3.B 4.A 5.D 6.A 7.C 8.A 9.C 10.A
 11.B 12.A 13.C 14.D 15.C 16.D 17.A 18.D 19.C 20.D
 21.D 22.A 23.A 24.D 25.A