Chuyên đề Hình học Lớp 12 - Chương 2: Mặt nón, trụ, cầu - Bài 1: Mặt nón tròn xoay

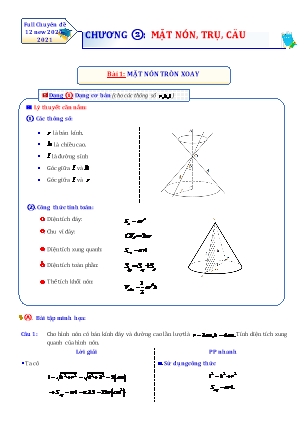
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ②: MẶT NÓN, TRỤ, CẦU
 Bài 1: MẶT NÓN TRÒN XOAY 
  Dạng ①: Dạng cơ bản (cho các thông số r,h,l )
 . Lý thuyết cần nắm:
 ①. Các thông số: 
 • r là bán kính.
 • h là chiều cao.
 • l là đường sinh 
 • Góc giữa l và h 
 • Góc giữa l và r
 ②. Công thức tính toán: 
 . Diện tích đáy: 2
 Sñ r
 . Chu vi đáy:
 CVđ 2πr 
 . Diện tích xung quanh: Sxq rl
 . Diện tích toàn phần:
 Stp Sxq Sñ
 . Thể tích khối nón: 1
 V r2h
 noùn 3
Ⓐ. Bài tập minh họa:
Câu 1: Cho hình nón có bán kính đáy và đường cao lần lượt là r 3cm,h 4cm. Tính diện tích xung 
 quanh của hình nón.
 Lời giải PP nhanh
Ta có  Sử dụng công thức
 2 2 2
 l h2 r 2 42 32 5 cm l h r
 2 Sxq rl.
 Sxq πrl π.3.5 15π cm 
 Câu 2: Cho hình nón có bán kính đáy và đường cao lần lượt là r 6cm,h 8cm. Tính diện tích toàn 
 phần của hình nón.
 Lời giải PP nhanh
Ta có  Sử dụng các công thức
 2 2 2
 l h2 r 2 62 82 10 cm l h r
 2
 2 2 2 Stp rl r .
 Stp πrl πr π.6.10 π.6 96π cm 
Câu 3: Cho khối nón có bán kính đáy và đường sinh lần lượt là r 3cm,l 5cm. Tính thể tích khối 
 nón.
 Lời giải PP nhanh trắc nghiệm
Ta có  Sử dụng công thức tính thể tích khối nón
 2 2 2 2 1
 h l r 5 3 4 cm V r 2h.
 3
 1 1
 V πr 2h π.32.4 12π cm3 
 3 3
Câu 4: Cho hình nón có đường cao bằng 2a và đường sinh bằng a 5 . Tính diện tích toàn phần của 
 hình nón.
 Lời giải PP nhanh trắc nghiệm
Ta có  Sử dụng công thức tính thể tích khối nón
 2 2 2
 2 2 r l h
 r l 2 h2 a 5 2a a
 2
 Stp rl r .
 2 2 2
 STP πrl πr π.a.a 5 π.a πa 5 1 
Câu 5: Hình nón có bán kính đáy là 4a, chiều cao là 3a. có diện tích xung quanh bằng:
 Ⓐ. 20 a2. Ⓑ. 40 a2. Ⓒ. 24 a2. Ⓓ. 12 a2.
 Lời giải PP nhanh trắc nghiệm
Chọn A  Sử dụng công thức tính
Ta có 2 2
 Sxq πrl πr r h
 l r 2 h2 4a 2 3a 2 5a
 2
 Sxq πrl π.4a.5a 20πa
Ⓑ.Bài tập rèn luyện:
Câu 1: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích xung 
 quanh Sxq của hình nón bằng:
 2
 Ⓐ. Sxq rl. Ⓑ. Sxq rh. Ⓒ. Sxq 2 rl. Ⓓ. Sxq r h.
Câu 2: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích toàn 
 phần Stp của hình nón bằng: 2 2 2 2
 Ⓐ. Stp rh r . Ⓑ. Stp 2 rl 2 r . Ⓒ. Stp rl 2 r . Ⓓ. Stp rl r .
Câu 3: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Thể tích của 
 khối nón bằng:
 1 1
 Ⓐ. V r 2h. Ⓑ.V r 2h. Ⓒ. V r 2l. Ⓓ. V r 2l.
 3 3
Câu 4: Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Đẳng thức 
 nào sau đây luôn đúng?
 1 1 1
 Ⓐ. r 2 h2 l 2. Ⓑ.l 2 h2 r 2. Ⓒ. . Ⓓ. l 2 hr.
 l 2 h2 r 2
Câu 5: Một hình nón có đường sinh l gấp đôi bán kính r của mặt đáy. Diện tích xung quanh của hình 
 nón là:
 1 1
 Ⓐ. S 2 r 2. Ⓑ. S 2 rl. Ⓒ. S r 2. Ⓓ. S rl.
 xq xq xq 2 xq 2
Câu 6: Một khối nón có đường cao a (cm) , bán kính r cm thì có thể tích bằng:
 1 1 1 1
 Ⓐ. V ra. Ⓑ.V r3. Ⓒ. V r2a. Ⓓ. V a2r.
 noùn 3 noùn 3 noùn 3 noùn 3
Câu 7: Một khối nón có thể tích bằng 4π và chiều cao bằng 3. Bán kính đường tròn đáy bằng:
 2 3 4
 Ⓐ. 2. Ⓑ. . Ⓒ. . Ⓓ. 1.
 3 3
 1
Câu 8: Một khối nón có diện tích xung quanh bằng 2 cm2 và bán kính đáy r cm. Khi đó độ dài 
 2
 đường sinh của khối nón là:
 Ⓐ. 3. Ⓑ. 4. Ⓒ. 2. Ⓓ. 1.
Câu 9: Thể tích của khối nón sẽ thay đổi như thế nào nếu tăng độ dài bán kính đáy lên hai lần mà vẫn 
 giữ nguyên chiều cao của khối nón?
 Ⓐ. Tăng 4 lần. Ⓑ.Giảm 2 lần. Ⓒ. Tăng 2 lần. Ⓓ. Không đổi.
Câu 10: Hình nón có diện tích xung quanh bằng 24 và bán kính đường tròn đáy bằng 3. Chiều cao 
 khối nón là:
 Ⓐ. 8. Ⓑ. 89. Ⓒ. 3. Ⓓ. 55.
 BẢNG ĐÁP ÁN
 1.A 2.D 3.B 4.B 5.A 6.C 7.A 8.B 9.A 10.D  Dạng ②: Thiết diện qua trục SO 
 -Phương pháp: 
 ❶. Thiết diện qua trục là tam giác vuông cân SAB
 l r 2
 ①. 
 h r
 2
 ②. Sxq r 2
 2 2 2
 ③. Stp r 2 r r ( 2 1)
 2 2
 ④. Diện tích thiết diện bằng STD r h
 1 1
 ⑤. Thể tích V r3 h3
 3 3
 ❷. Thiết diện qua trục là tam giác đều SAB 
 l 2r
 ①. l 3
 h 
 2
 2
 ②. Sxq 2 r
 2 2 2
 ③. Stp 2 r r 3 r
 l 2 3
 ④. Diện tích thiết diện: S r 2 3
 TD 4
 1 l3 3
 ⑤. Thể tích: V r 2h 
 3 24
 A - Bài tập minh họa: 
 Câu 1: Một hình nón có thiết diện qua trục là tam giác đều cạnh bằng 2a. Tính diện tích xung quanh 
 và diện tích toàn phần của hình nón đó.
 Lời giải PP nhanh trắc nghiệm
 Ta có thiết diện qua trục của hình nón là tam giác đều l 2r
 cạnh bằng 2a nên l 2r 2a l 2a;r a. 2
  Sxq 2πr
  S πrl 2πa2.
 xq 2
  Stp 3πr
 2 2
  Stp πrl πr 3πa
 Câu 2: Một khối nón có thiết diện qua trục là tam giác đều cạnh bằng a. Tính thể tích của khối nón 
 đó.
 Lời giải PP nhanh trắc nghiệm
 Ta có thiết diện qua trục của hình nón là tam giác đều l3 3 a3 3
 a  V .
 cạnh bằng a nên l 2r a l a;r . 24 24
 2
 a 3
 h l 2 r 2 
 2
 2 3
 1 2 1 a a 3 πa 3
 V πr h π. . 
 3 3 2 2 24
 Câu 3: Một khối nón có thiết diện qua trục là tam giác vuông cân cạnh có cạnh huyền bằng 2a. Tính 
 diện tích xung quanh, diện tích toàn phần, diện tích thiết diện và thể tích của khối nón đó.
 Lời giải PP nhanh trắc nghiệm
 Ta có thiết diện qua trục của hình nón là tam giác  h r
 vuông cân có cạnh huyền bằng 2a nên
 2
  Sxq πr 2
 2r 2a r h a.
 2 2 2
 2 2  Stp πr 2 πr πr 2 1 
  Sxq πr 2 πa 2
 2 2
 2 2 2  Diện tích thiết diện bằng STD r h
  Stp πr 2 πr πa 2 1 
 1 3 1 3
 Diện tích thiết diện bằng S r 2 a2  Thể tích V πr πh
 TD 3 3
 1 1
 Thể tích V πr3 πa3
 3 3
 B - Bài tập rèn luyện:
 Câu 1: Thiết diện qua trục của một hình nón là tam giác vuông có cạnh huyền là 2a 2. Thể tích khối 
 nón giới hạn bởi hình nón đó là
 2 a3 2 2 a3 3 4 a3 3
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. 2 a3 2.
 3 3 3
 Câu 2: Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a . Thể tích của khối 
 nón là
 a3 3 a3 3 a3 3 a3 3
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 9 6 3 12
 Câu 3: Cho hình nón tròn xoay có đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy 
 bằng 60. Diện tích xung quanh Sxq của hình nón và thể tích V của khối nón lần lượt là
 6 6
 Ⓐ. S a2 và V a3 . Ⓑ. S 2 a2 và V a3 .
 xq 24 xq 12
 6 a2 6
 Ⓒ. S 3 a 2 và V a3 . Ⓓ. S và V a3 .
 xq 4 xq 2 8
 Câu 4: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông 
 cân có cạnh góc vuông bằng a . Tính thể tích V của khối nón được tạo nên bởi hình nón đã 
 cho.
 2 a3 2 a3 2 a3 2 a3
 Ⓐ. V = . Ⓑ.V = . Ⓒ. V = . Ⓓ. V = .
 10 12 4 6 Câu 5: Cắt một hình nón bằng một mặt phẳng qua trục của nó được thiết diện là tam giác đều cạnh 
 bằng a. Tính thể tích V của khối nón theo a.
 a3 3 a3 3 a3 3 a3 3
 Ⓐ. V . Ⓑ.V . Ⓒ. V . Ⓓ. V .
 24 3 6 12
Câu 6: Cho hình nón có thiết diện qua trục là tam giác vuông có cạnh huyền bằng a 2 . Tính diện tích 
 xung quanh S xq của hình nón đó.
 a2 2 a2 2 a2 2 a2 3
 Ⓐ. S Ⓑ. S Ⓒ. S Ⓓ. S 
 xq 2 xq 6 xq 3 xq 3
Câu 7: Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng a. Tính 
 diện tích Stp toàn phần của hình nón đó:
 2
 a 2 8 a2 2
 Ⓐ. S .Ⓑ. S .
 tp 2 tp 2
 a2 2 1 a2 2 4 
 Ⓒ. S . Ⓓ. S .
 tp 2 tp 2
Câu 8: Cho hình nón đỉnh S biết rằng nếu cắt hình nón bởi một mặt phẳng đi qua trục ta được một 
 tam giác vuông cân có cạnh huyền bằng a 2 . Diện tích xung quanh của hình nón là:
 a2 2a2
 Ⓐ. S . Ⓑ. S . Ⓒ. S a2 . Ⓓ. S 2 a2 .
 xq 2 xq 2 xq xq
Câu 9: Hình nón N có đỉnh S , tâm đường tròn đáy là O , góc ở đỉnh bằng 120. Một mặt phẳng qua 
 S cắt hình nón N theo thiết diện là tam giác vuông SAB . Biết rằng khoảng cách giữa hai 
 đường thẳng AB và SO bằng 3. Tính diện tích xung quanh S xq của hình nón N 
 Ⓐ. Sxq 27 3 . Ⓑ. Sxq 18 3 . Ⓒ. Sxq 9 3 . Ⓓ. Sxq 36 3 .
Câu 10: Cho tam giác ABC vuông cân tại A biết BC a 2 . Gọi I là trung điểm của BC . Tính diện 
 tích toàn phần của khối nón tròn xoay sinh ra khi cho ABC quay quanh AI một góc 360 .
 2 2
 2 2 1 a a2 2 2 1 a
 Ⓐ. 2 2 1 a2 . Ⓑ. . Ⓒ. . Ⓓ. .
 2 2 2
 BẢNG ĐÁP ÁN
 1.A 2.C 3.A 4.B 5.A 6.A 7.C 8.B 9.B 10.D  Dạng ③: Khối nón sinh bởi tam giác quay quanh các trục
 -Phương pháp: 
 ①.Quay tam giác SOA vuông tại O S
 quanh trục SO
 • r OA là bán kính.
 • h SO là chiều cao.
 • l SA là đường sinh A O
 ②.Quay tam giác SOA vuông tại O quanh A
 trục OA
 • r SO là bán kính.
 • h OA là chiều cao.
 • l SA là đường sinh 
 S O
A - Bài tập minh họa: 
Câu 1: Cho tam giác ABC đều cạnh bằng a, đường cao AH. Tính diện tích xung quanh của hình nón 
 được tạo thành khi quay tam giác ABC quanh AH.
 Lời giải PP nhanh trắc nghiệm
Khi quay tam giác ABC quanh AH ta được một hình  Quay quanh cái gì thì nó là trục; Cạnh 
nón có: đáy chính là đường kính.
 Trục là AH.
 a
Bán kính đáy r = .
 2
 Đường sinh l = AB = AC = a.
Suy ra diện tích xung quanh của hình nón là
 pa2
 Sxq = prl =
 2
Câu 2: Cho tam giác ABC vuông tại C có các cạnh AC = 2a;BC = a . Tính thể tích của khối nón được 
 tạo thành khi quay tam giác ABC quanh AC
 Lời giải PP nhanh trắc nghiệm
Khi quay tam giác ABC quanh AC ta được một hình nón  Quay quanh cái gì thì nó là trục; Cạnh 
có: đáy chính là đường kính.
 Trục là AC nên h = AC = 2a. .
 Bán kính đáy r = BC= a..
 Suy ra thể tích của khối nón là
 1 2pa3
 V = pr2h =
 3 3
Câu 3: Cho tam giác ABC vuông tại C có các cạnh AC = 2a;BC = a . Tính thể tích vật thể tròn xoay 
 được tạo thành khi quay tam giác ABC quanh AB.
 Lời giải PP nhanh trắc nghiệm
Gọi H là hình chiếu vuông góc của C lên AB, ta có:  Khi quay một tam giác vuông quanh 
 cạnh huyền thì
 AC.BC 2a 5
 CH = = 1 2
 AC2 + BC2 5 V = p.(đ­êngcaotamgi¸c) .c¹nhhuyÒn
 3
 AB = AC2 + BC2 = a 5
Khi quay tam giác ABC quanh AC ta được một vật thể 
tròn xoay gồm 2 hình nón có:
 Hình nón thứ 1 có trục là AH nên
 h1 = AH & r1 = CH
 1 1
 Þ V = pr 2h = p.CH 2 .AH (1)
 1 3 1 1 3
 Hình nón thứ 2 có trục là BH nên
 h2 = BH & r2 = CH
 1 1
 Þ V = pr 2h = p.CH 2 .BH (2)
 2 3 2 2 3
Suy ra thể tích của vật thể tròn xoay là
 1 1
 V = V + V = p.CH 2 .(AH + BH) = p.CH 2 .AB
 1 2 3 3
 4pa3 5
 = .
 15
B - Bài tập rèn luyện:
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC a 6 . 
 Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn 
 xoay. Thể tích của khối nón tròn xoay đó là
 4 a3 a3 2 a3 3 a3 3
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 3 3 3 6 .
Câu 2: Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện 
 tích xung quanh của hình nón đó là
 1 3
 Ⓐ. a2 . Ⓑ. 2 a2 . Ⓒ. a2 . Ⓓ. a2
 2 4
Câu 3: Hình ABCD khi quay quanh BC thì tạo ra Ⓐ. Một hình trụ. Ⓑ.Một hình nón.
 Ⓒ. Một hình nón cụt. Ⓓ. Hai hình nón.
Câu 4: Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra 
 bởi đoạn thẳng AC của hình lập phương ABCD. A B C D có cạnh b khi quay xung quang trục 
 AA . Diện tích S là
 Ⓐ. b2 . . Ⓑ. b2 2.. Ⓒ. b2 3.. Ⓓ. b2 6.
Câu 5: Trong không gian, cho tam giác ABC cân tại A , AB a 10, BC 2a . Gọi H là trung điểm của 
 BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH .
 Ⓐ. V 2 a3 . Ⓑ.V 3 a3 . Ⓒ. V 9 a3 . Ⓓ. V a3 .
Câu 6: Cho tứ diện đều ABCD . Khi quay tứ diện đó quanh trục AB có bao nhiêu hình nón khác nhau 
 được tạo thành?
 Ⓐ. Một. Ⓑ.Hai.
 Ⓒ. Ba. Ⓓ. Không có hình nón nào.
 1
Câu 7: Cho hình tròn có bán kính là 6 . Cắt bỏ hình tròn giữa hai bán kính
 4
 OA,OB rồi ghép hai bánkính đó lại sao cho thành một hình nón (như hình vẽ). Thể tích khối 
 nón tương ứng đó là
 81 7 9 7
 Ⓐ. . Ⓑ. .
 8 8
 81 7 9 7
 Ⓒ. . Ⓓ. .
 4 2
Câu 8: Cho một hình cầu bán kính 5 cm, cắt hình cầu này bằng một 
 mặt phẳng sao cho thiết diện tạo thành là một đường kính 4
 cm. Tính thể tích của khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm hình cầu đã cho. (lấy 
 3,14, kết quả làm tròn tới hàng phần trăm).
 Ⓐ. 50,24 (ml). Ⓑ.19,19 (ml). Ⓒ. 12,56 (ml). Ⓓ. 76,74 (ml).
Câu 9: Hình chữ nhật ABCD có AB 6, AD 4 . Gọi M , N, P,Q lần lượt là trung điểm bốn cạnh 
 AB, BC,CD, DA. Cho hình chữ nhật ABCD quay quanh QN , tứ giác MNPQ tạo thành vật 
 tròn xoay có thể tích bằng
 Ⓐ. V 8 . Ⓑ.V 6 . Ⓒ. V 4 . Ⓓ. V 2 .
Câu 10: Cho một hình thang cân ABCD có các cạnh đáy AB 2a ,CD 4a, cạnh bên AD BC 3a. 
 Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của 
 nó.
 14a3 2 56a3 2 14a3 28a3 2
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 3 3 3 3
 BẢNG ĐÁP ÁN 1.A 2.C 3.D 4.D 5.D 6.B 7.A 8.B 9.A 10.A
  Dạng ④: Bài toán thiết diện qua đỉnh và mối liên hệ với góc hoặc khoảng cách
 -Phương pháp: 
 ①. Thiết diện qua đỉnh của hình nón: mp(P) đi qua 
 đỉnh của hình nón và cắt mặt nón theo 2 đường sinh 
 Thiết diện cũng là tam giác cânSAB .
 ②. Khoảng cách từ tâm của đáy O đến thiết diện:
 + Casio:
 d O;(SAB) OK
 1
 OK 
 1: SO2 1:OH 2
 ③.Góc giữa SO vá thiết diện SAB:
 ·SO;(SAB) S·OH
 OH
 tan S·OH 
 SO
 ④.Góc giữa (SAB) và đáy:
 ·SAB;(OAB) S·HO
 SO
 tan S·HO 
 OH
A - Bài tập minh họa: 
Câu 1: Thiết diện qua trục một hình nón là một tam giác vuông cân có cạnh huyền bằng 2 3 . Thể 
 tích của khối nón này là
 Ⓐ. 3 . Ⓑ.3 3 . Ⓒ. 3 . Ⓓ. 3 2
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Ghi nhớ công thức: