Chuyên đề Hình học Lớp 11 - Chương 4 - Bài 3: Hai mặt phẳng vuông góc (Có lời giải)

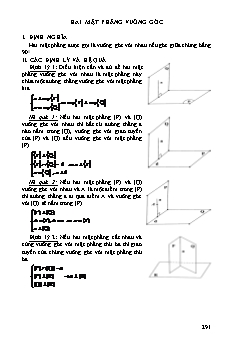
 HAI MẶT PHẲNG VUÔNG GÓC
I. ĐỊNH NGHĨA
 Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 
900.
II. CÁC ĐỊNH LÝ VÀ HỆ QUẢ
 Định lý 1: Điều kiện cần và đủ để hai mặt Q
phẳng vuông góc với nhau là mặt phẳng này 
chứa một đường thẳng vuông góc với mặt phẳng a
kia.
 a  mp P 
 mp P  mp Q P
 a  mp Q 
 Hệ quả 1: Nếu hai mặt phẳng (P) và (Q) 
vuông góc với nhau thì bất cứ đường thẳng a Q
nào nằm trong (Q), vuông góc với giao tuyến 
của (P) và (Q) đều vuông góc với mặt phẳng a
(P). 
 P  Q P
 P  Q d a  P d
 a  Q , a  d
 Hệ quả 2: Nếu hai mặt phẳng (P) và (Q) 
vuông góc với nhau và A là một điểm trong (P) P
thì đường thẳng a đi qua điểm A và vuông góc a
với (Q) sẽ nằm trong (P). A
 (P)  (Q) Q
 A (P),A a a  (P) d
 a  (Q)
 Định lý 2: Nếu hai mặt phẳng cắt nhau và 
cùng vuông góc với mặt phẳng thứ ba thì giao P Q
tuyến của chúng vuông góc với mặt phẳng thứ a
ba.
 (P)  (Q) a
 (P)  (R) a  (R) R
 (Q)  (R)
 291 HÌNH LAÊNG TRUÏ ÑÖÙNG, HÌNH HOÄP CHÖÕ NHAÄT, HÌNH 
 LAÄP PHÖÔNG
 ĐỊNH NGHĨA:
 Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với các 
mặt đáy. Độ dài cạnh bên được gọi là chiều cao của hình lăng trụ đứng.
 + Hình lăng trụ đứng có đáy là tam giác, tứ giác, ngũ giác, ... được gọi là 
hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác, hình lăng trụ đứng 
ngũ giác,...
 + Hình lăng trụ đứng có đáy là một đa giác đều được gọi là hình lăng trụ 
đều. Ta có các loại lăng trụ đều như hình lăng trụ tam giác đều , hình lăng 
trụ tứ giác đều , hình lăng trụ ngũ giác đều ...
  Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp 
đứng.
  Hình lăng trụ đứng có đáy là hình chữ nhật được gọi là hình hộp chữ 
nhật.
  Hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình 
vuông được gọi là hình lập phương.
 HÌNH CHOÙP ÑEÀU VAØ HÌNH CHOÙP CUÏT ÑEÀU
 HÌNH CHÓP ĐỀU
 Một hình chóp được gọi là hình chóp đều nếu nó có đáy là một đa giác 
đều và có chân đường cao trùng với tâm của đa giác đáy.
 Nhận xét:
 + Hình chóp đều có các mặt bên là những tam giác cân bằng nhau. Các 
mặt bên tạo với mặt đáy các góc bằng nhau.
 + Các cạnh bên của hình chóp đều tạo với mặt đáy các góc bằng nhau.
 HÌNH CHÓP CỤT ĐỀU 
 Phần của hình chóp đều nằm giữa đáy và một thiết diện song song với 
đáy cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều.
 PHƯƠNG PHÁP CHỨNG MINH HAI MẶT PHẲNG VUÔNG GÓC
 Cách 1: Ta chứng minh mặt phẳng này chứa một đường thẳng vuông 
 góc với mặt phẳng kia.
 Cách 2: Ta chứng minh góc giữa chúng là 900 .
 Câu 1: Cho tứ diện ABCD có AB  (BCD). Trong tam giác BCD vẽ các 
 đường cao BE và DF cắt nhau tại O. Trong mp(ACD) vẽ DK  AC. Gọi 
 H là trực tâm của tam giác ACD.
 a). Chứng minh (ACD)  (ABE) và (ACD)  (DFK).
 b). Chứng minh OH  (ACD).
292 LỜI GIẢI
a). Chứng minh (ACD)  (ABE) và A
 (ACD)  (DFK).
 CD  BE gt 
 CD  AB do AB  BCD CD  ABE , 
 BE,AB  ABE 
 mà CD  ACD ACD  ABE K H
 DF  BC , DF  AB B D
 DF  ABC 
 BC,AB  ABC F O
 DF  AC AC  ABC 1 . E
 C
 AC  DF do 1 , AC  DK gt 
 AC  DFK , 
 DF,DK  DFK 
 mà AC  ACD ACD  DFK 
b.Chứng minh OH  (ACD).
 Ta có CD  ABE CD  OH vì OH  ABE * 
 Ta có AC  DKF AC  OH vì OH  DKF * * 
 OH  CD , OH  AC
 Từ * , * * : OH  ACD .
 CD,AC  ACD 
 ABE  DFK OH
 Cách khác Ta có : ABE  ACD . Suy ra OH  ACD .
 DEF  ACD 
 Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, SAC 
 là tam giác đều và nằm trong mp vuông góc với (ABC). Gọi I là trung 
 điểm của SC.
 a). Chứng minh (SBC)  (SAC). b) Chứng minh 
 (ABI)  (SBC).
 LỜI GIẢI S
 Gọi H trung điểm của AC . Ta có SAC đều 
nên SH  AC , AI  SC .
 SAC  ABC AC
 I
 Có SAC  ABC SH  mp ABC .
 A B
 SH  AC , SH  SAC 
 H
 C 293 BC  AC gt , BC  SH
 Có BC  SAC mà BC  SBC SBC  SAC 
 AC,SH  SAC 
 AI  SC gt 
 Có AI  BC BC  SAC AI  SBC mà AI  ABI ABI  SBC 
 SC,BC  SBC 
 Câu 3: Cho hình chóp S.ABCD có đáy là hình thoi cạnh a và SA = SB = SC 
 = a.
 a). Chứng minh (SBD)  (ABCD). b). Chứng minh tam giác SBD 
 vuông.
 LỜI GIẢI S
 Gọi H là hình chiếu vuông góc của 
S trên mặt phẳng (ABCD) . 
 Vì SA SB SC nên HA HB HC
 Suy ra H nằm trên đường trung trực 
của đoạn AC, vậy H BD . D A
a). Chứng minh (SBD)  (ABCD).
 H
 AC  BD
 O
 AC  SO 
 C B
 BD,SO  mp SBD 
 AC  mp SBD mà AC  ABCD ABCD  SBD .
b) Chứng minh tam giác SBD vuông.
 Ta có ba tam giác : SAC BAC DAC c.c.c . Suy ra ba đường trung 
tuyến xuất phát từ 3 đỉnh tương ứng bằng nhau thì bằng nhau , nghĩa là 
SO BO DO .
 1
Trong tam giác SBD có SO là đường trung tuyến và SO BD SBD vuông 
 2
tại O. 
 Câu 5: Cho tam giác đều ABC. Trên đường thẳng d vuông góc với 
 mp(ABC) tại A lấy điểm S. Gọi D là trung điểm của BC.
 a). Chứng minh (SAD)  (SBC). 
 b). Kẻ CI  AB, CK  SB. Chứng minh SB  (ICK).
 c). Kẻ BM  AC, MN  SC. Chứng minh SC  BN.
 d). Chứng minh (CIK)  (SBC) và (BMN)  (SBC).
 e). MB cắt CI tại G, CK cắt BN tại H. Chứng minh GH  (SBC).
 LỜI GIẢI
 S
294
 N
 K H
 M
 C
 A
 G
 I D
 B a) Chứng minh (SAD)  (SBC). Vì 
 ABC đều nên AD  BC 
 Ta có
 BC  AD , BC  SA
 BC  SAD , 
 AD,SA  SAD 
 mà BC  SBC 
 SAD  SBC 
b). Chứng minh SB  (ICK). 
 CI  AB , CI  SA
 CI  SAB CI  SB 1 
 AB,SA  SAB 
 SB  CK gt 
 có SB  CI do 1 SB  CIK 
 CK,CI  CIK 
c). Chứng minh SC  BN. Vì ABC đều nên BM  AC .
 BM  AC , BM  SA
 Có BM  SAC BM  SC 2 
 AC,SA  SAC 
 SC  MN gt 
 Có SC  BM do 2 SC  BMN SC  BN
 MN,BM  BMN 
d). Theo câu b) SB  CIK mà SB  SBC SBC  CIK 
 Theo câu c) SC  BMN mà SC  SBC SBC  BMN 
 CIK  BMN HG
e). Ta có : CIK  SBC HG  SBC .
 BMN  SBC 
 Câu 6: Cho hình chóp S.ABCD có đáy là hình thoi tâm O. Hai mặt 
 phẳng (SAC) và (SBD) cùng vuông góc với đáy ABCD .
 a). Chứng minh (SAC)  (SBD). 
 b). Từ O kẻ OK  BC. Chứng minh BC  (SOK).
 c). Chứng minh (SBC)  (SOK). 
 d). Kẻ OH  SK tại H. Chứng minh OH  (SBC).
 LỜI GIẢI S
a). Chứng minh (SAC)  (SBD). 
 Ta có :
 295
 A D
 H
 O
 B
 K C SAC  SBD SO
 SAC  ABCD SO  ABCD .
 SBD  ABCD 
 AC  BD ABCD hình thoi 
 Có AC  SO vì SO  ABCD 
 BD,SO  SBD 
 AC  SBD mà AC  SAC SAC  SBD .
b). Chứng minh BC  (SOK).
 BC  OK gt , BC  SO SO  ABCD 
 BC  SOK .
 OK,SO  SOK 
 BC  SOK 
c). Chứng minh (SBC)  (SOK). vì SBC  SOK 
 BC  SBC 
d). Chứng minh OH  (SBC).
 OH  SK gt , OH  BC BC  SOK 
 OH  SBC 
 SK,BC  SBC 
 Câu 7: Cho hình vuông ABCD. Gọi S là điểm trong không gian sao cho 
 SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy 
 (ABCD) .Gọi H và I lần lượt là trung điểm của AB và BC.
 a). Chứng minh (SAB)  (SAD) và (SAB)  (SBC).
 b). Chứng minh (SHC)  (SDI).
 LỜI GIẢI
 Vì tam giác SAB đều nên SH  AB . S
 SAB  ABCD AB
 Có SAB  ABCD SH  ABCD 
 SH  SAB , SH  AB
a). Chứng minh (SAB)  (SAD) và (SAB)
 A D
 (SBC). 1
 AD  AB gt H
 AD  SH SH  ABCD AD  SAB ,
 1 1
 AB,SH  SAB B I C
 mà AD  SAD SAD  SAB 
 Chứng minh hoàn toàn tương tự , ta chứng minh được SBC  SAB .
b). Chứng minh (SHC)  (SDI).
 ¶ ¶ ¶ µ 0 ¶ µ 0
 Có BCH CDI c.g.c C1 D1 , mà D1 I1 90 C1 I1 90 . 
296 Vậy HC  DI
 DI  CH
 Có DI  SH SH  ABCD DI  SHC , 
 CH,SH  SHC 
 mà DI  SDI SDI  SHC 
 Câu 9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA  đáy. 
 a 3a
 Gọi M, N là các điểm thuộc BC và CD sao cho BM = , DN . 
 2 4
 Chứng minh (SAM)  (SMN).
 S
 LỜI GIẢI
 Pitago cho các tam giác vuông ABM, 
CMN, ADN . Ta có:
 2 2 
 2 2 2 2 a 5a
 AM AB BM a 
 2 4 
 A D
 2 2 2 
 2 2 2 a a 5a 
 MN CM CN 
 2 4 16 
 2
 2 N
 2 2 2 2 3a 25a
 AN AD DN a 
 B C
 4 16  M
 AM2 MN2 AN2 . 
 Theo định lý đảo Pitago thì AMN vuông tại M. . Suy ra MN  AM .
 MN  AM
 MN  mp SAM . Mà MN  mp SMN SAM  SMN .
 MN  SA
 GOÙC GIÖÕA HAI MAËT PHAÚNG 
 PHƯƠNG PHÁP GIẢI TOÁN
 Q
 Để tìm góc giữa hai mặt phẳng , đầu tiên d
tìm giao tuyến của hai mặt phẳng . Sau đó 
tìm hai đường thẳng lần lượt thuộc hai mặt A
phẳng cùng vuông góc với giao tuyến tại P
một điểm . Góc giữa hai mặt phẳng là góc d'
giữa hai đường thẳng vừa tìm .
Những trường hợp đặc biệt đề hay ra : B
 297
 C A
 H
 D Trường hợp 1 : Hai tam giác cân ACD và 
BCD có chung cạnh đáy CD . Gọi H trung điểm 
của CD , thì góc giữa hai mặt phẳng (ACD) và 
(BCD) là góc A· HB .
 A
 Trường hợp 2 : Hai tam giác ACD và BCD bằng 
nhau có chung cạnh CD . Dựng 
AH  CD BH  CD . Vậy góc giữa hai mặt phẳng 
(ACD) và (BCD) là góc A· HB .
 B D
 H
 C
 Trường hợp 3 : Khi xác định góc giữa hai mặt phẳng quá khó , ta nên sử 
dụng công thức sau :
 d A,mp Q 
 sin 
 d A,a 
 Với là góc giữa hai mặt phẳng (P) và mặt phẳng (Q). A là một điểm 
thuộc mặt phẳng (P) và a là giao tuyến của hai mặt phẳng (P) và (Q).
 Trường hợp 4 : Có thể tìm góc giữa hai mặt phẳng bằng công thức 
S' S.cos 
 Trường hợp 5 : Tìm hai đường thẳng d và d' lần lượt vuông góc với mặt 
phẳng (P) và mặt phẳng (Q) . Góc giữa hai mặt phẳng là góc giữa d và d' . 
 Trường hợp 6 : CÁCH XÁC ĐỊNH GÓC GIỮA MẶT PHẲNG BÊN 
VÀ MẶT PHẲNG ĐÁY
 BƯỚC 1: XÁC DỊNH GIAO TUYẾN d của mặt bên và mặt đáy.
 BƯỚC 2 : TỪ HÌNH CHIẾU VUÔNG GÓC CỦA ĐỈNH , DỰNG 
AH  d .
 BƯỚC 3 : GÓC CẦN TÌM LÀ GÓC S·HA .
 Với S là đỉnh , A là hình chiếu vuông góc của đỉnh trên mặt đáy.
Ví dụ điển hình : Cho hình chóp S.ABC có SA vuông góc với đáy (ABC) 
 S
.Hãy xác định góc giữa mặt bên (SBC) và mặt đáy (ABC).
 Ta có BC là giao tuyến của mp(SBC) và (ABC).
 Từ hình chiếu của đỉnh là điểm A , dựng AH  BC .
 BC  SA
 Vì BC  SAH BC  SH . C
 BC  AH A
 H
298
 B Kết luận góc giữa hai mặt phẳng (SBC) và (ABC) là góc S·HA .
 Câu 1: Cho tứ diện ABCD có AD  (BCD) và AB = 3a. Biết BCD là tam 
 giác đều cạnh 2a. Tính góc giữa hai mặt phẳng :
 a). (ACD) và (BCD). b). (ABC) và (DBC)
 LỜI GIẢI
 A
a). Tính góc giữa hai mặt phẳng 
(ACD) và (BCD).
 Vì AD vuông góc với mặt phẳng (BCD) 
nên hai mặt phẳng (ACD) và (BCD) vuông 
góc với nhau , suy ra góc giữa chúng bằng 
900 .
b). Tính góc giữa hai mặt phẳng 
 B
(ABC) và (BCD). D
 BC  AD
 Dựng DE  BC tại E , ta có E
 BC  DE
 BC  mp SBC BC  AE . C
 Hai mặt phẳng (ABC) và (BCD) có BC là giao tuyến và hai đường thẳng 
DE , AE lần lượt thuộc hai mặt phẳng cùng vuông góc với giao tuyến BC . 
Nên góc giữa (ABC) và (DBC) là góc giữa DE và AE chính là góc A· ED .
 BC 3
 Tam giác BCD đều nên có DE a 3 .
 2
 ABD vuông tại D có AD AB2 DB2 9a2 4a2 a 5 .
 Trong ADE vuông tại D có 
 AD a 5 15 15 
 · · .
 tan AED AED arctan 
 DE a 3 3 3 
 Câu 2: Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a , SA 
 vuông góc với đáy ABCD , SA a 3 . Tính góc giữa các cặp mặt phẳng 
 sau :
 a). (SAB) và (SBC) b). (SAD) và (SCD) c). (SAB) và 
 (SCD) 
 d). (SBC) và (SAD) e). (SBD) và (ABCD) f). (SBD) và 
 (SAB) 
 g). (SBC) và (ABCD) h). (SCD) và (ABCD) i). (SBD) và 
 (SBC)
 k). (SBC) và (SCD)
 299 LỜI GIẢI
a). Góc giữa (SAB) và (SBC)
 S
 BC  AB
 Ta có 
 BC  SA
 BC  SAB SBC  SAB BC  SBC . H
 Vậy góc giữa mặt phẳng (SBC) và mặt 
 0
phẳng (SAB) bằng 90 . I J
b). Góc giữa (SAD) và (SCD) D
 A K
 CD  AD
 Ta có O
 CD  SA
 B
 CD  SAD SCD  SAD CD  SCD . C
 Vậy góc giữa mặt phẳng (SCD) và mặt phẳng (SAD) bằng 900 . 
c). Góc giữa (SAB) và (SCD) Dựng AH  SD H SD . 
 Ta có AH  SD vµ AH  CD v× CD  SAD , tõ ®ã AH  SCD (2)
 Ngoài ra ta có AD  SAB . Sử dụng cách xác định góc trường hợp 5 , thì 
góc giữa hai mặt phẳng (SAB) và (SCD) là góc giữa hai đường thẳng AH và 
AD chính là góc H· AD .
 Ta có D· AH D· SA ( vì cùng phụ với góc S·AH ). 
 AD 1
 tan D· SA D· SA 300 .
 AS 3
 · 0
 Kết luận SAB , SCD D· AH 30 .
d). Góc giữa (SBC) và (SAD)
 Dựng AI  SB I SB . Ta có 
 AI  SB vµ AI  CB v× CB  SAB , tõ ®ã AI  SBC 
 Ngoài ra ta có AB  SAD . Sử dụng cách xác định góc trường hợp 5 , thì 
góc giữa hai mặt phẳng (SBC) và (SAD) là góc giữa hai đường thẳng AI và 
AB chính là góc B· AI .
 Ta có B· AI B· SA ( vì cùng phụ với góc S· AI ). 
 AB 1
 Có tan B· SA B· SA 300 .
 AS 3
 · 0
 Kết luận SBC , SAD B· AI 30 .
e). Góc giữa (SBD) và (ABCD)
300