Chuyên đề Hình học Lớp 11 - Chương 3: Quan hệ song song trong không gian - Phần 3 (Có lời giải)

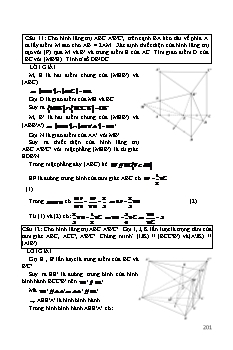
 Câu 11: Cho hình lăng trụ ABC.A'B'C', trên cạnh BA kéo dài về phía A 
ta lấy điểm M sao cho AB = 2AM. Xác định thiết diện của hình lăng trụ 
tạo với (P) qua M và B' và trung điểm E của AC. Tìm giao điểm D của 
BC với (MB'E). Tính tỉ số DB/DC .
 LỜI GIẢI A' C'
 M, E là hai điểm chung của (MEB') và 
(ABC) 
 MEB'  ABC ME . 
 B'
 Gọi D là giao điểm của ME và BC N
 Suy ra MEB'  BCC'B' DB' . M
 C
 M, B' là hai điểm chung của (MEB') và A E
 D
(ABB'A') MEB'  ABB'A' MB' . F
 Gọi N là giao điểm của AA' với MB'. 
 B
 Suy ra thiết diện của hình lăng trụ 
ABC.A'B'C' với mặt phẳng (MEB') là tứ giác 
EDB'N.
 Trong mặt phẳng đáy (ABC) kẻ EF // BC F AB . 
 1
 EF là đường trung bình của tam giác ABC có EF BC 
 2
 (1) 
 MF EF 2 2
 Trong MBD có EF BD (2)
 MB BD 3 3
 2 1 3 DB
 Từ (1) và (2) có: BD BC BD BC 3 .
 3 2 4 DC
Câu 12: Cho hình lăng trụ ABC.A'B'C'. Gọi I, J, K lần lượt là trọng tâm của 
tam giác ABC, ACC', A'B'C'. Chứng minh” (IJK) // (BCC'B') và(A'JK) // 
(AIB').
 LỜI GIẢI
 Gọi E , E' lần lượt là trung điểm của BC và A' C'
B'C'. K
 E'
 Suy ra EE' là đường trung bình của hình 
bình hành BCC'B' nên BB' // EE' . B'
 J
 Mà BB' // AA' AA' // EE' 
 AEE'A' là hình bình hành . A M C
 I
 Trong hình bình hành AEE'A' có: E
 B
 201 A'K A'E'
 IK // EE' (1) 
 AI AE
 Gọi M trung điểm của AC. 
 MI MJ 1
 Trong MBC' có: IJ // BC' (2)
 MB MC' 3
 Từ (1) và (2) suy ra IJK // BCC'B' .
 Mặt phẳng (A'CE') cũng là mặt phẳng (A'JK). 
 Mặt phẳng (AEB') cũng là mặt phẳng (AIB').
 Trong mp(BCC'B') có EB' // CE' . 
 Vì AEE'A' là hình bình hành A'E' // AE . (4)
 Từ (3) và (4) suy ra A'JK // AIB' .
 Câu 13: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, M' lần lượt là 
 trung điểm của các cạnh BC, B'C'.
 a) Chứng minh AM song song với A'M'.
 b) Tìm giao điểm của đường thẳng A'M và mặt phẳng (AB'C').
 c) Tìm giao tuyến d của hai mặt phẳng (AB'C') và (BA'C').
 d) Tìm giao điểm G của đường thẳng của đường thẳng d với mặt phẳng 
(AM'M). Chứng minh G là trọng tâm của tam giác AB'C'.
 LỜI GIẢI A' C'
a) Vì MM' là đường trung bình của M'
   B'
 hình bình hành BCC'B' nên MM' BB' .
     G
 Mà BB' AA' . Từ đó suy ra: MM' AA' . K
 I
 Vậy: AMM'A' là hình bình hành
 .
 AM // A'M' A C
b) Tìm giao điểm của đường thẳng A'M và M
mặt phẳng (AB'C') . B
 Trong mặt phẳng (AMM'A'), gọi: K A'M  AM'
 K A'M
 Có: K A'M  AB'C' .
 K AM',AM'  AB'C' 
c) Tìm giao tuyến d của hai mặt phẳng (AB'C') và (BA'C') .
 Trong mặt phẳng (ABB'A'), gọi:.I BA' AB'
 I BA',BA'  BA'C' 
 Có: I BA'C'  AB'C' 
 I AB',AB'  AB'C' 
 Và C' BA'C'  AB'C' .
 Vậy giao tuyến d của hai mặt phẳng (AB'C') và (BA'C') là IC'.
202 Trong mặt phẳng (AB'C') gọi G C'I  AM'
 G C'I
 Có G C'I  AMM' .
 G AM',AM'  AMM' 
 G là giao điểm của hai đường trung tuyến C'I và AM' của tam giác 
AB'C'. Vậy: G là trọng tâm của tam giác AB'C'.
Câu 14: Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Các 
 mặt bên ABB'A', ACC'A' là hình vuông có tâm lần lượt là I và J. Gọi 
O là 
 tâm đường tròn tam giác ABC.
 a) Chứng minh IJ song song với mặt phẳng (ABC) .
 b) Xác định thiết diện của lăng trụ với mặt phẳng (IJO). Tính diện tích 
thiết diện đó theo a.
 LỜI GIẢI
a) Chứng minh IJ song song với mặt phẳng A' L C'
(ABC). M
 Ta có IJ là đường trung bình của tam giác 
 J
A'BC nên IJ // BC. B'
 Mà BC  ABC . Suy ra IJ P ABC .
 I
b) Xác định thiết diện của lăng trụ với mặt phẳng K
(IJO). A C
 O là điểm chung của hai mặt phẳng (IJO) và O
(ABC), nên giao tuyến của chúng đi qua O và H
song song với BC, giao tuyến này cắt AB, AC lần B
lượt tại H và K.
 HI là giao tuyến của (IJO) với (ABB'A'), gọi 
M HI  A'B' .
 KJ là giao tuyến của (IJO) với (ACC'A'), gọi 
L KJ  A'C' .
 Từ đó suy ra ML là giao tuyến của (IJO) và (A'B'C'), vì IJ // B'C' suy ra 
ML // B'C' // IJ.
 Kết luận thiết diện cần tìm là hình thang HKLM ( vì HK // LM // BC ) 
(1)
 Ta có ABB'A', ACC'A' là hình vuông và AH = AK , A'M = A'L.
 Suy ra MH = LK (2)
 Từ (1) và (2) suy ra: HKLM là hình thang cân 
 A' a/3 M 2a/3 B'
 Trong ABC có HK // BC nên: 
 AH HK 2 2a
 HK .
 AB BC 3 3
 a I
 203
 a/3
 A E H B
 Hình 2 IJ là đường trung bình của HKLM, có:
 HK LM
 IJ 
 2 .
 2a a
 LM 2IJ HK BC HK a 
 3 3
 Vẽ lại mặt bên ABB'A' như hình 2. 
 a2 a 10 M L
 Ta có: MH ME2 EH2 a2 .
 9 3
 Vẽ lại thiết diện như hình 3.
 2a a a a
 Ta có 2HI HK ML HI . 
 3 3 3 6
 H K
 10.a2 a2 a 39 I Hình 3
 Và MI MH2 HI2 
 9 36 6
 Diện tích hình thang cân HKLM:
 1 1 2a a a 39 a2 39
 SHKLM HK LM .MI . .
 2 2 3 3 6 12
 Câu 15: Cho hình lăng trụ ABC.A'B'C' 
 a) Tìm giao tuyến của hai mặt phẳng (AB'C') và (BA'C').
 b) Gọi M, N lần lượt là hai điểm bất kỳ trên AA' và BC. Tìm giao điểm 
của B'C' với mặt phẳng (AA'N) và giao điểm của MN với (AB'C').
 LỜI GIẢI
a) Tìm giao tuyến của hai mặt phẳng (AB'C') và (BA'C')
 C' là điểm chung thứ nhất của hai mặt phẳng (AB'C') và (BA'C').
 Trong mặt phẳng (ABB'A') gọi G là giao điểm của AB' và BA'. Suy ra G 
là điểm chung thứ hai của hai mặt phẳng (AB'C') và (BA'C') .
 Kết luận AB'C'  BA'C' GC' .
 A' C'
b) Tìm giao điểm của B'C' với mặt phẳng J
(AA'N) và giao điểm của MN với (AB'C').
 Chọn mặt phẳng (BCC'B') chứa B'C'. M B'
 N AA'N  BCC'B' K
 G
 Ta có : AA' // BB'
 AA'  AA'N ,BB'  BCC'B' A C
 N
 AA'N  BCC'B' Nx Nx // AA' // BB' .
 B
 Gọi J Nx  B'C' J B'C' AA'N .
 Chọn mặt phẳng (ANJA') chứa MN. 
 Tìm giao tuyến của mặt phẳng (ANJA') và (AB'C').
204 Ta có: A ANJA'  AB'C' (1) 
 J ANJA' 
 Và: J ANJA'  AB'C' (2)
 J B'C'  AB'C' 
 Từ (1) và (2) suy ra AJ ANJA'  AB'C' . 
 Trong mp(ANJA') gọi K MN  AJ K MN  AB'C' .
 Câu 16: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, M' lần lượt là 
 trung điểm của các cạnh BC, B'C'.
 a) Chứng minh AM song song với A'M'.
 b) Tìm giao điểm của đường thẳng A'M và mặt phẳng (AB'C').
 c) Tìm giao tuyến d của hai mặt phẳng (AB'C') và (BA'C').
 d) Tìm giao điểm G của đường thẳng d với mặt phẳng (AM'M). Chứng 
minh G là trọng tâm của tam giác AB'C'.
 LỜI GIẢI
a) Vì MM' là đường trung bình của hình bình A' C'
     M'
hành BCC'B' nên MM' BB' , mà BB' AA' từ 
   B'
đó suy ra MM' AA' , vậy AMM'A' là hình bình G
hành, suy ra . K
 AM // A'M' I
b) Tìm giao điểm của đường thẳng A'M và mặt 
phẳng (AB'C') . A C
 Trong mặt phẳng (AMM'A'), gọi: K A'M  AM' M
 K A'M B
 Có: K A'M  AB'C' .
 K AM',AM'  AB'C' 
c) Tìm giao tuyến d của hai mặt phẳng (AB'C') và (BA'C').
 Trong mặt phẳng (ABB'A') gọi I BA' AB'
 I BA',BA'  BA'C' 
 Có: I BA'C'  AB'C' 
 I AB',AB'  AB'C' 
 Và C' BA'C'  AB'C' 
 Vậy giao tuyến d của hai mặt phẳng (AB'C') và (BA'C') là IC'.
d) Trong mặt phẳng (AB'C') gọi G C'I  AM'
 G C'I
 Có: G C'I  AMM' .
 G AM',AM'  AMM' 
 G là giao điểm của hai đường trung tuyến C'I và AM' của tam giác 
AB'C'. Vậy G là trọng tâm của tam giác AB'C'.
 205 Câu 17: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N lần lượt là trung điểm 
của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
 a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
 b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính 
chất gì? 
 c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình 
hộp.
 LỜI GIẢI
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
 Gọi O và O' lần lượt là tâm của hai đáy (ABCD) và (A'B'C'D').
 Suy ra: OO' BDD'B'  ACC'A' . A' D'
 O'
 Gọi I MN  OO' MN,OO'  ACC'A' .
 B'
 I MN,MN  MNP C'
 Ta có: M
 Q x
 I OO',OO'  BDD'B' I
 E
 I MNP  BDD'B' (1)
 N P
 A D
 P MNP 
 Ta có: 
 P DD',DD'  BDD'B' O
 B
 P MNP  BDD'B' C
 Từ (1) và (2) suy ra: MNP  BDD'B' PI . 
 Gọi Q PI  BB' Q BB' MNP .
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện là tứ giác MNPQ.
 NP và QM là giao tuyến của mặt phẳng (MNP) với hai mặt phẳng song 
song với nhau là (ABB'A') và (CDD'C'). Nên suy ra NP // QM (3)
 Lý luận tương tự thì MP // QN (4) 
 Từ (3) và (4) suy ra: Thiết diện MNPQ là hình bình hành.
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD)
 Trong mặt phẳng bên (CDD'C') gọi E CD  NP . 
 Vì MN là đường trung bình của hình bình hành ACC'A', suy ra MN // 
AC. Từ đó suy ra giao tuyến của hai mặt phẳng (MNP) và mặt phẳng 
(ABCD) qua E và song song với MN // AC.
Câu 18: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, G' lần lượt là trọng 
tâm của ABC và A'B'C'. Một mặt phẳng P cắt các cạnh AA', BB', CC', GG' 
lần lượt tại A1,B1,C1,G1 . Chứng minh: 
a) GG' song song và bằng cạnh bên của lăng trụ.
b) G1 là trọng tâm của A1B1C1 .
206 1 1
c) G G' A A' B B' C C' ; G G A A B B C C .
 1 3 1 1 1 1 3 1 1 1
 LỜI GIẢI
a) GG' song song và bằng cạnh bên của lăng trụ.
 Gọi M và M' theo thứ tự là trung điểm của BC và B'C'. Nên MM' là 
đường trung bình của hình bình hành BCC'B'.
 Suy ra: MM' // BB' // CC' B' A'
 N'
 và MM' = BB' = CC' (1) G'
 M'
 Vì ABC.A'B'C' là hình lăng trụ nên: AA' // B1
BB' và AA' = BB' C ' 
 A1
(2) M1
 G1 N1
 Từ (1) và (2) suy ra: 
 AMM'A' là hình bình hành và có: C1
 AG A'G' 2 B A
 (tính chất trọng tâm) N
 G
 AM A'M' 3 M
 Nên GG' // AA' và GG' = AA'.
 C
b) Gọi M1 MM' B1C1 MM',B1C1  BCC'B' . 
 Tính chất hình bình hành thì M1 là trung điểm của B1C1 (3)
 Ta có:A1M1 A1B1C1  AA'M'M . 
 G1 chính là giao điểm của A1M1 với GG'.
 AG A1G1 2
 Vì MM1 // GG1 // AA1 suy ra (4)
 AM A1M1 3
 Từ (3) và (4) suy ra: G1 là trọng tâm của tam giác A1B1C1 .
c) Gọi N , N' lần lượt trung điểm của AG và A'G'. 
 Dễ chứng minh được NN' // GG' //AA' 
 Gọi N1 là giao điểm của NN' và A1G1 suy ra N1 trung điểm của A1G1.
 Ta có: G1G' là đường trung bình của hình thang M1M'N'N1;
 N1N' là đường trung bình của hình thang A1A'G'G1;
 M1M' là đường trung bình của hình thang B1B'C'C1.
 1
 Nên:G G' M M' N N' (1)
 1 2 1 1
 1
 N N' A A' G G' (2)
 1 2 1 1
 1
 M M' B B' C C' (3)
 1 2 1 1
 1 2
 Từ (1) và (2): G G' A A' M M' 4 
 1 3 1 3 1
 207 1
 Thay (3) vào (4) ta được: G G' A A' B B' C C' .
 1 3 1 1 1
 1
 Chứng minh tương tự:.G G A A B B C C 
 1 3 1 1 1
Câu 19: Cho hình hộp ABCD.A'B'C'D' .
a) Chứng minh rằng hai mặt phẳng (BDA') và (B'D'C) song song với nhau.
b) Chứng minh rằng đường chéo AC' đi qua trọng tâm G 'và G "lần lượt 
của hai tam giác BDA' và B'D'C .
c) Chứng minh G' và G " chia đoạn thẳng AC' thành ba phần bằng nhau.
d) Gọi E, F, G, H, K, L lần lượt là trung điểm của BC, CD, DD', D'A', A'B', 
B'B. Chứng minh sáu điểm ở trên đồng phẳng.
 Lời giải: A' H D'
 K O'
a)CDA'B' là hình bình hành nên DA' // CB' (1)B' G
 C'
 BDD'B' là hình hành nên: G''
 I
 BD // B'D' (2) G'
 L A D
 Từ (1) và (2) suy ra (A'BD) / /(B'D'C) .
 O F
 B E C
b) Gọi O và O' lần lượt là tâm của ABCD và
 A' O' C'
 A'B'C'D' .
 Trong mp(ACC'A') , AC' cắt A'O và CO' tại G''
 G' và G " (theo thứ tự). G' I
 O là trung điểm của BD nên A'O là trung 
tuyến của tam giác và A C
 BDA' G' A'O O Hình 2
(1)
 A'C' // OA nên: 
 G'O OA 1
 G'A' 2G'O (2) (2)
 G'A' A'C' 2
 Từ (1) và (2) suy ra: G' là trọng tâm của tam giác A'BD 
 Tương tự, G " là trọng tâm của tam giác B'D'C .
c) Tam giác ACG" , OG' là đường trung bình nên G' là trung điểm của 
AG" AG' G'G" (3)
 Tương tự, ta có C'G" G"G' (4)
 Từ (3) và (4) suy ra AG' G'G" G"C' 
 Vậy G' và G " chia AC' thành ba phần bằng nhau (đpcm).
208 d) Vì có FG // CD', HK // B'D', LE // B'C ba đường thẳng FG, HK, LE cùng 
song song với mp(CB'D').
 Tương tự ba đường thẳng EF, GH, KL cùng song song với mp(A'BD).
 Mà (A'BD) // (CB'D') suy ra sáu điểm E, F, G, H, K, L đồng phẳng.
Câu 20: Cho hình hộp ABCD.A'B'C'D' . Gọi M, N lần lượt là trung điểm 
của CD và CC' .
a) Xác định đường thẳng qua M cắt AN và cắt A'B .
 IM
b) Gọi I, J lần lượt là giao điểm của với AN và A'B . Hãy tìm tỉ số .
 IJ
 LỜI GIẢI B' C'
a) Giả sử đã dựng được đường thẳng cần 
tìm cắt cả AN và A'B . 
 Gọi I, J lần lượt là giao điểm của với A' D' N
AN và A'B . J
 N'
 Δ I
 Xét phép chiếu song song lên mặt phẳng B
 C
 ABCD theo phương chiếu A'B . I'
 Khi đó ba điểm J, I, M lần lượt có hình A
chiếu là B,I',M . D
 Do đó: ba điểm B,I',M thẳng hàng. 
 Gọi N' là hình chiếu của N thì AN' là hình chiếu của AN. 
 Vì I thuộc AN nên I' thuộc AN' . Vậy I' là giao điểm của BM và .AN'
 Từ phân tích trên ta có thể dựng đường thẳng theo các bước sau đây:
 Lấy giao điểm I' của AvàN ' . BM
 Trong mp(ANN') dựng II'/ /NN' (đã có NN'/ /CD' ) cắt AN tại I .
 Vẽ đường thẳng MI , đó là đường thẳng cần tìm.
b) Dễ chứng minh được, đường thẳng nói trên cắt A'B .
 Dễ thấy MC CN' suy ra MN' CD AB .
 Do đó I là trung điểm của BM .
 Mặt khác: II'/ /JB , nên II' là đường trung bình của tam giác MBJ .
 IM
 Suy ra: IM IJ 1 
 IJ
Câu 21: Cho hình hộp ABCD.A'B'C'D' . Hãy xác định đường thẳng cắt 
cả hai đường thẳng AC' và BA' đồng thời song song với B'D' . Gọi I,J lần 
 AI
lượt là giao điểm của với AC và' BA . Tính' tỉ số .
 AC'
 A
 LỜI GIẢI D
 209
 B
 C
 I
 Δ J
 A'
 D'
 B'
 C'
 K a) Giả sử đã xác định được đường thẳng 
 cắt AC' và BA' lần lượt tại I và J.
 Xét phép chiếu song song lên mp 
(ABB'A') theo phương chiếu D'B' . 
 Khi đó, hình chiếu của ba điểm A,I,C' 
lần lượt là ba điểm thẳng hàng A,J,K . 
Mặt khác: J thuộc BA' , nên J chính là 
giao điềm của AK và BA' .
 Từ đó, ta có cách dựng đường thẳng 
theo các bước sau đây:
 Dựng điểm K là hình chiếu của C (theo' phương chiếu D’B’).
 Lấy giao điểm J của AK và BA' .
 Qua J dựng đường thẳng // C'K ( đã có C'K // B'D' ), ta được 
đường thẳng cần tìm.
b) Dễ thấy A'B' B'K A'K 2AB (do A'B' AB ).
 AI AB 1
 Vì AB / /A'K .
 JK A'K 2
 AI AJ 1 AI 1
 Mặt khác: IJ / /C'K .
 IC' JK 2 AC' 3
 Câu 22: Cho hình hộp ABCD.A'B'C'D' .
a) Chứng minh rằng đường chéo B'D cắt mp(A'BC') tại điểm G sao cho 
 1
BG GD và G là trọng tâm tam giác A'BC' .
 2
b) Chứng minh rằng (D'AC) // (BA'C') và trọng tâm G' của cũngD'AC 
 2
nằm trên B'D và B'G' B'D .
 3
c) Gọi P, Q, R lần lượt là các điểm đối xứng của điểm B qua' A, D', C . 
Chứng minh rằng (PQR) // (BA'C'). 
d) Chứng minh rằng D là trọng tâm tứ diện B'PQR .
 LỜI GIẢI R
a) Gọi O' là giao điểm của 
A'C' và B'D' . Khi đó: 
  
(A'BC') (BDD'B') BO' . P B
 C
 Gọi G là giao điểm của 
B'D và BO' thì G chính là 
 A D
giao điểm của B'D với mp
 G
(A'BC') . C'
 B'
210 O'
 A' D'
 Q