Chuyên đề Hình học Lớp 11 - Chương 3: Quan hệ song song trong không gian - Phần 2 (Có lời giải)

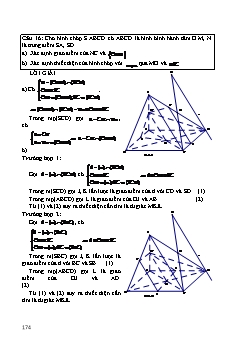
 Câu 16: Cho hình chóp S.ABCD có ABCD là hình bình hành tâm O.M, N 
 là trung điểm SA, SD.
 a). Xác định giao điểm của NC và OMD 
 b). Xác định thiết diện của hình chóp với mp qua MO và PSC .
 LỜI GIẢI E
 D (OMD) (SCD)
 a) Có OM PSC (OMD) (SCD) SDx POM PSC
 OM  (OMD),SC  (SCD)
 D (OMD) (SCD)
 K
 OM PSC (OMD) (SCD) Dx POM PSC M N
   x
 OM (OMD),SC (SCD)Trong mp(SCD) gọi E CN  Dx , 
 có 
 A D
 E CN
 E CN (OMD) . L
 E Dx  (OMD) O J
 b) B C
 Hinh 1
 Trường hợp 1:
 d ( ) (SCD)
 Gọi d ( ) (SCD) , có OM PSC d POM PSC .
 OM  ( );SC  (SCD)
 Trong m(SCD) gọi J, K lần lượt là giao điểm của d với CD và SD (1).
 Trong mp(ABCD) gọi L là giao điểm của OJ và AB (2).
 Từ (1) và (2) suy ra thiết diện cần tìm là từ giác MKJL.
 E
 Trường hợp 2:
 Gọi d ( ) (SBC) , có
 d ( ) (SBC) S
 OM PSC d POM PSC .
 OM  ( );SC  (SBC)
 M N
 x
 Trong m(SBC) gọi J, K lần lượt là K
 giao điểm của d với BC và SB (1).
 L
 Trong mp(ABCD) gọi L là giao A D
 điểm của OJ và AD 
 (2). O
 B J C
 Từ (1) và (2) suy ra thiết diện cần Hinh 2
 tìm là từ giác MKJL.
 174 Câu 17: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a; SAD là 
tam giác vuông cân tại A; M là một điểm trên SC; là qua M và song 
song với SA và BC cắt các cạnh SB,AB,CD lần lượt tại N,P,Q .
a) Hình MNPQ là hình gì? Tính diện tích MNPQ trong trường hợp SAC là 
tam giác vuông tại A,SM x 0 x a 3 
b) CM : PSD 
c) Gọi I MQ  NP . Tìm tập hợp các điểm I khi M di động SC.
 LỜI GIẢI S
 ( ) (SBC) MN
 Có MN PBC (1). I
 BC P( ); BC  (SBC)
 x
  
 ( ) (SAB) NP M
 Có NP PSA (2). N
 SA P( );SA  (SAB)
 D
 A
 ( ) (ABCD) PQ
 Có PQ PBC (3).
 BC P( ); BC  (ABCD) P Q
 B C
 Từ (1), (2) và (3) suy ra tứ giác MNPQ là hình thang, vì có 
MN PPQ PBC ( ) .
 NP PSA
 Ngoài ra có PQ PAD PBC NP  PQ ( ) 
 SA  AD
 Từ ( ) và ( ) suy ra MNPQ là hình thang vuông tại N và P.
 Vì SAC vuông tại A nên có SC SA2 AC2 a2 2a2 a 3 .
 SN MN SM x x
 Trong SBC có MN và 
 SB BC SC a 3 3
 BN SN x a 3 x
 1 1 .
 BS SB a 3 a 3
 PN BN a 3 x a 3 x
 Trong SAB có PN .
 SA BS a 3 3
 Vì ABCD là hình vuông và PQ PBC PQ BC a .
 x a 3 x
 a 
 PQ MN PN 3 3
 Vậy S 
 MNPQ 2 2
 175 CM BN BP BP CQ CM CQ
 b) Có , ngoài ra MQ PSD (Theo 
 CS BS BA BA CD CS CD
 định lý đảo Ta lét).
 Mà MQ  ( ) SD P( ) .
 S (SAB) (S CD)
 c) Có AB PCD (SAB) (S CD) Sx PAB PCD .
 AB  (SAB),CD  (S CD)
 I NP  (SAB)
 Có MQ  NP I , có I (SAB) (S CD) . Hay I Sx . Suy 
 I MQ  (S CD)
 ra I chạy trên tia Sx cố định khi M di động trên SC.
 Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, 
 AB 2a,BC 3a , biết hai tam giác SAB và SCD đều. Điểm M thuộc cạnh 
 SA và SM x 0 x 2a . Mặt phẳng (MBC) cắt SD tại N.
 a) Xác định giao tuyến của hai mặt phẳng (SAC) và (SBD); (SAB) và 
 (SCD).
 b) Chứng minh tứ giác BMNC là hình thang cân.
 c) Tính diện tích tứ giác BMNC theo a và x.
 LỜI GIẢI
 a) Có S, O là hai điểm chung của hai mặt phẳng 
 S
 (SAC) và (SBD). Do đó:
 (SAC) (SBD) SO x N y
 M
 S (SAB) (SCD)
 D
 Có AB PCD (SAB) (SCD) Sx PAB PCDA
 AB  (SAB);CD  (SCD)
 S (SAB) (SCD) O
 AB PCD (SAB) (SCD) Sx PAB PCD B C
 AB  (SAB);CD  (SCD) M (M BC) (SAD)
 b) Có BC PAD (M BC) (SAD) My PBC PAD .
 BC  (M BC); AD  (SAD)
 Trong (SAD) gọi N SD  My N SD (MBC) .
 Từ đó suy ra BCNM là hình thang (với MN PBC ).
 MN SM x x 3x
 Có MN PAD MN .AD .
 AD SA 2a 2a 2
 M N
 Xét tam giác SBM và tam giác SCN có:
 176 B H C SB SC
 SM SN SBM SCN BM CN 
 · · 0
 BSM CSN 60
 MN PBC
 Tứ giác BMNC có MN BC BMNC là hình thang cân.
 BM CN
c) Áp dụng định lý cosin vào SBM ta có: 
 BM2 SB2 SM2 2SB.SMcos600 
 1
 4a2 x2 2.2ax. BM 4a2 x2 2ax CN
 2
 3x
 3a 
 BC MN 6a 3x
 Dựng MH  BC tại H. Ta có BH 2 .
 2 2 4
 2
 2 2 2 2 6a 3x 1 2 2
 MH BM BH 4a x 2ax 28a 7x 4ax 
 4 4
 Diện tích tứ giác BMNC là: 
 3x 1
 3a 28a2 7x2 4ax
 MN BC MH 2 4 6a 3x 2 2
 S . 28a 7x 4ax
 2 2 16
Câu 19: Cho hình vuông ABCD cạnh a, tâm O. Gọi S là một điểm ở ngoài 
mặt phẳng (ABCD) sao cho SB = SD. Gọi M là điểm tùy ý trên AO với 
AM = x. Mặt phẳng ( ) qua M song song với SA và BD cắt SO , SB , AB 
tại N, P , Q .
 a) Tứ giác MNPQ là hình gì?
 b) Cho SA = a. Tính diện tích MNPQ theo a và x. Tính x để diện tích lớn 
nhất.
 LỜI GIẢI S
a) Tứ giác MNPQ là hình gì?
 Ta có: SB = SD SBC SDC c.c.c 
 · · N
 SCB SCD P
 Gọi I là trung điểm SC thì IBC IDC c.g.c I
 IB ID . A D
 Vậy IBD cân tại I IO  BD. Q M
 Mà OI // SA SA  BD (*) O
 B C
 177 ( ) // BD
 Ta có: BD  (ABO) MQ // BD (1) 
 ( )  (ABO) MQ
 ( ) // BD
 Tương tự: BD  (SBO) NP // BD (2)
 ( )  (SBO) NP
 Từ (1) và (2), suy ra MQ // NP // BD (3)
 ( ) // SA
 Ta có: SA  (SAO) MN // SA (4)
 ( )  (SAO) MN
 ( ) // SA
 Tương tự : SA  (SAB) PQ // SA (5)
 ( )  (SAB) PQ
 Từ (4) và (5), suy ra MN // PQ // SA (6)
 Từ (3), (6) và (*), suy ra MNPQ là hình chữ nhật.
b) Tính diện tích MNPQ theo a và x:
 Ta có: SMNPQ MQ.MN .
 Tính MQ: Xét tam giác AQM:
 Ta có: Aµ 450 , Qµ 450 , Mµ 900 AQM cân tại M. Vậy MQ = AM = x.
 Tính MQ: Xét tam giác SAO: 
 a 2
 x
 MN OM OM
 Ta có: MN // SA MN AS. a. 2 a x. 2
 AS OA OA a. 2
 2
 1
 .SMNPQ MQ.MN x.(a x. 2) x. 2(a x. 2)
 2
 Áp dụng bất đẳng thức Côsi cho 2 số dương x. 2 và (a x. 2 ):
 2
 x 2 a x 2 a2 a2
 x 2 a x 2 x 2 a x 2 SMNPQ
 2 4 4 2
 a a. 2
 Đẳng thức xảy ra khi x. 2 a x. 2 x 
 2. 2 4
 M là trung điểm AO
178 a. 2
 Vậy: x thì S đạt giá trị lớn nhất.
 4 MNPQ
 Câu 20: Cho hình chóp SABCD có đáy là hình vuông cạnh a. Trên cạnh 
AB lấy một điểm M với AM = x. Gọi ( ) là mặt phẳng qua M và song song 
với mặt phẳng (SAD) cắt SB, SC, và CD lần lượt tại N, P, Q.
 a) Tìm thiết diện của ( ) với mặt phẳng hình chóp. Thiết diện là hình 
gì?
 b) Tìm quĩ tích giao điểm I của MN và PQ khi M di động trên đoạn AB.
 c) Cho S·AD 900 và SA = a. Tính diện tích của thiết diện theo a và x. 
 2
 Tìm x để diện tích của thiết diện bằng 3a .
 8
 LỜI GIẢI
a) Tìm thiết diện của ( ) với mặt phẳng S I x S0
hình chóp:
 N
 Vì mp // SAD mp // với 
 P
mọi đường thuộc mặt phẳng (SAD).
 Tìm giao tuyến của mặt phẳng ( ) 
và mặt phẳng (ABCD). 
 A B
 Có M là điểm chung của hai mặt M
phẳng mp và mp (ABCD), vì 
mp // AD, nên giao tuyến của chúng 
qua M và song song với AD, giao tuyến D Q C
này cắt CD tại điểm Q.
 Tương tự:
 Mặt phẳng ( ) và mặt phẳng (SAB) có M là điểm chung và // SA , 
nên giao tuyến của chúng là MN với MN // SA và N SB .
 Mặt phẳng ( ) và mặt phẳng (SBC) có N là điểm chung và 
 // AD // BC, nên giao tuyến của chúng là NP với NP // BC và P SC 
(2)
 Mặt phẳng ( ) và mặt phẳng (SCD) có 2 là điểm chung là P, Q. 
 Vậy: giao tuyến của chúng là PQ.
 Suy ra: thiết diện cần tìm là MNPQ.
 Từ (1) và (2) thì MQ // PN . Vậy MNPQ là hình thang.
b) Tìm quĩ tích giao điểm I của MN và PQ khi M di động trên đoạn AB:
 179 AB // DC
 Ta có: AB  (SAB) , DC  (SCD) (SAB)  (SCD) Sx Sx // AB // CD 
 S (SAB)  (SCD)
 I PQ  (SCD)
 Mà: I (SAB)  (SDC). Vậy I Sx.
 I MN  (SAB)
 Giới hạn quĩ tích : Khi M  A thì I  S . Còn khi M  B thì I  S0
c) Tính diện tích của thiết diện theo a và x: 
 Ta có:SMNPQ S IMQ S INP S SAD S INP (Vì IMQ = SAD (c.g.c))
 1
 Tính S : Ta có SAD vuông cân tại A, do đó:.S .a2
 SAD SAD 2
 Tính S INP : Xét tam giác SBC, tam giác SBS0 và tam giác SAB có:
 NI SN
 NI // S0B (1)
 S0B SB
 PN SN
 PN // BC (2)
 BC SB
 AM SN
 MN // SA (3)
 AB SB
 NI PN AM
 Từ (1), (2) và (3), ta được: NI PN AM x .
 S0B BC AB
 INP vuông cân tại N, vì NI // SA, PN // AD và SA  AD.
 1
 Do đó: S .x2 . 
 INP 2
 1 1 1
 Vậy: diện tích thiết diện: S .a2 .x2 (a2 x2 )
 MNPQ 2 2 2
 3.a2 1 3.a2 3.a2
 Để S (a2 x2 ) x2 a2 
 MNPQ 8 2 8 4
 a2 a
 x2 . x 
 4 2
Câu 21: Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi M là 
trung điểm của SC, (P) là mặt phẳng qua AM và song song với BD.
 a) Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (P).
 b) Gọi E, F lần lượt là giao điểm của (P) với các cạnh SB và SD. Hãy tìm 
tỉ số diện tích của tam giác SME với tam giác SBC và tỉ số diện tích của tam 
giác SMF và tam giác SCD.
180 c) Gọi K là giao điểm của ME và CB, J là giao điểm của MF và CD. Hãy 
chứng minh 3 điểm K, A, J nằm trên một đường thẳng song song với EF và 
tìm tỉ số EF .
 KJ
 LỜI GIẢI S
a) Gọi O AC  BD mp SAC  mp SBD SO .
 Gọi I AM  SO AM,SO  mp SAC M
 F
 I mp SBD .
 I E
 I P  SBD J C
 D
 BD // mp P 
 O
 BD  SBD 
 A B
 SBD  P Ix Ix // BD 
 Gọi E Ix  SB,F Ix  SD . K
 Suy ra: E, F cũng là giao điểm của SB, SD với mặt phẳng (P).
 Vậy: Thiết diện cần tìm là tứ giác AEMF.
 SI 2
b) Để ý ta có: I là trọng tâm của tam giác SAC nên: .
 SO 3
 SE SF SI 2
 Xét tam giác SBD có EF song song với BD ta có: .
 SB SD SO 3
 1 1
 SM.SE.sin B· SC SM.SF.sin D· SC
 S SE SM 1 S SF SM 1
 SME 2 . ; SMF 2 . 
 S 1 SB SC 3 S 1 SD SC 3
 SBC SC.SB.sin B· SC SCD SC.SD.sin D· SC
 2 2
c)K EM  BC K mp P  ABCD (1)
 J FM  CD J mp P  ABCD (2)
  (3)
 A mp P ABCD 3 
 Từ (1), (2), (3) suy ra ba điểm K, J, K thuộc giao tuyến của mp (P) và 
mp (ABCD).
 mp P  mp ABCD 
 Ta có: // BD .
 BD // mp P 
 Xét tam giác MJK có: EF // JK vì JK // BD,EF // BD : 
 ME MF MI EF 1 EF 1
 . Vậy .
 MK MJ MA JK 3 KJ 3
 181 Câu 22: Cho hình chóp S.ABCD có G là trọng tâm ABC. Gọi M, N, P, 
Q, R, H lần lượt là trung điểm của SA, SC, CB, BA, QN, AG.
 a) Chứng minh rằng: S, R, G thẳng hàng và SG = 2MH = 4RG.
 b) G' là trọng tâm SBC. Chứng minh rằng GG' // (SAB), GG' // (SAC).
 c) Mặt phẳng ( ) qua GG' và song song BC. Xác định thiết diện của hình 
chóp tạo bởi mặt phẳng ( ).
 LỜI GIẢI
a) Chứng minh rằng: S , R , G thẳng hàng S
và SG = 2MH = 4RG.
 Gọi E trung điểm của GC .
 Trong QNE có RG là đường trung M
bình của tam giác nên có: 
 N
  1  
 RG NE (1) S K
 2 R G'
 A T
 D
 Trong SCG có: NE là đường trung L
bình của tam giác nên có: H
   Q
 G E
 SG 2NE (2) F C
 P
 Từ (1) và (2) suy ra ba điểm G, R, S B
thẳng hàng và GS = 4GR.
 Trong SAG có HM là đường trung bình của tam giác nên có GS 2HM .
b) Chứng minh rằng: GG' // (SAB); GG' // (SAC).
 PG PG' 1
 Trong tam giác SAP có: GG' // SA .
 PA PS 3
 Hai mặt (SAB) và (SAC) cùng chứa SA. 
 Suy ra GG' // (SAB), GG' // (SAC).
c) Xác định thiết diện của hình chóp tạo bởi mặt phẳng ( )
 Vì // BC , nên cắt mặt phẳng đáy (ABCD) theo giao tuyến qua 
G và song song với BC. Giao tuyến này cắt AB tại F, cắt AD tại L. 
 Vì GG' // SA nên cắt mặt phẳng (SAB) theo giao tuyến qua F và 
song song với SA. Giao tuyến này cắt SB tại T.
 Vì GG' // SA nên cắt mặt phẳng (SAD) theo giao tuyến qua F và 
song song với SA. Giao tuyến này cắt SB tại T.
 TG' là giao tuyến của mặt phẳng với mặt phẳng (SBC), giao tuyến 
này cắt SC tại S.
 Thiết diện cần tìm là ngũ giác FLKST .
BÀI 3
 HAI MAËT PHAÚNG SONG SONG
182 Định lí 1:
 Nếu mặt phẳng chứa hai đường thẳng 
 M
cắt nhau a,b và a,b cùng song song với mặt a b
phẳng  thì song song với  . α
 Phương pháp chứng minh hai mặt phẳng 
song song:
Ta phải chứng minh có hai đường thẳng cắt β
nhau thuộc mặt phẳng này lần lượt song song 
với mặt phẳng kia.
Định lí 2:
 A
 Qua một điểm nằm ngoài một mặt phẳng α
cho trước có một và chỉ một mặt phẳng song 
song với mặt phẳng đã cho.
Hệ quả: β
 Nếu đường thẳng d song song với mặt 
phẳng thì trong có một đường thẳng 
song song với d và qua d có duy nhất một 
mặt phẳng song song với .
 Phương pháp chứng minh đường thẳng d α
song song với : Ta phải chứng minh d 
 d
thuộc  và  // d // . β
 Hệ quả 2:
 Hai mặt phẳng phân biệt cùng song song 
với mặt phẳng thứ ba thì song song với nhau. α
Hệ quả 3:
 Cho điểm A không nằm trên mặt phẳng A
 . Mọi đường thẳng đi qua A và song song β
với đều nằm trong mặt phẳng đi qua A và 
 γ
song song với .
 a
Định lí 3: α
Cho hai mặt phẳng song song. Nếu một mặt 
 b
phẳng cắt mặt phẳng này thì cũng cắt mặt β
phẳng kia và hai giao tuyến song song với nhau.
 b
 Hệ quả: a
 A'
 A
 α 183
 B'
 B
 β