Chuyên đề Giải tích Lớp 12 - Chương 3: Nguyên hàm. Tích phân. Ứng dụng - Bài 4: Tích phân từng phần (Có đáp án)

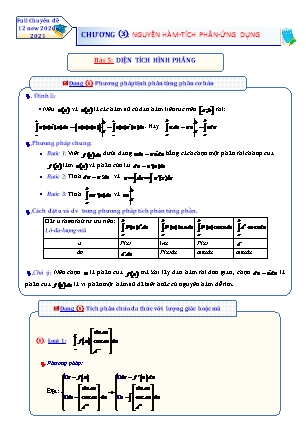
 Full Chuyên đề 
12 new 2020-
 2021 CHƯƠNG ③: NGUYÊN HÀM-TÍCH PHÂN-ỨNG DỤNG
 Bài 5: DIỆN TÍCH HÌNH PHẲNG 
  Dạng ①: Phương pháp tính phân từng phần cơ bản
 . Định lí: 
  Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên a;b thì:
 b b b b b b
 u(x)v'(x)dx u(x)v(x) v(x)u'(x)dx . Hay udv uv vdu 
 a a 
 a a a a
 .Phương pháp chung:
 • Bước 1: Viết f (x)dx dưới dạng udv uv'dx bằng cách chọn một phần thích hợp của 
 f (x) làm u(x) và phần còn lại dv v '(x)dx
 • Bước 2: Tính du u 'dx và v dv v '(x)dx
 b b
 • Bước 3: Tính vu '(x)dx và uv
 a a
 .Cách đặt u và dv trong phương pháp tích phân từng phần.
 Đặt u theo thứ tự ưu tiên: b b b b
 P(x)exdx P(x) ln xdx P(x) cosxdx ex cosxdx
 Lô-đa-lượng-mũ a a a a
 u P(x) lnx P(x) ex
 dv exdx P(x)dx cosxdx cosxdx
 .Chú ý: Nên chọn u là phần của f (x) mà khi lấy đạo hàm thì đơn giản, chọn dv v'd xlà 
 phần của f (x)dx là vi phân một hàm số đã biết hoặc có nguyên hàm dễ tìm.
  Dạng ①: Tích phân chứa đa thức với lượng giác hoặc mũ
  sin ax 
 ①. Loại 1: f x cos ax dx 
 ax
 e 
 .Phương pháp: 
 gu f x gdu f ' x dx
 sin ax sin ax 
 Đặt: . 
 gdv cos ax dx gv cos ax dx
 ax ax 
 e e 
 A - Bài tập minh họa: 
 2
Câu 1: Tính tích phân I xex dx .
 1
 Ⓐ. I e2 . Ⓑ. I e2 . Ⓒ. I e . Ⓓ. I 3e2 2e .
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Tính tích phân
 u x du dx
 Đặt x x
 dv e dx v e
 2 2
 I xexdx xex 2 exdx 2e2 e ex 2
 1 1
 1 1 .
 2e2 e e2 e e2
 + Kiểm tra các đáp án:
 2
 A e 0 (đúng).
 1
Câu 2: Tính tích phân I (x 2)e2xdx .
 0
 5 3e2 5 3e2 5 3e2 5 3e2
 Ⓐ. I . Ⓑ. I . Ⓒ. I . Ⓓ. I .
 4 4 4 4
 Lời giải PP nhanh trắc nghiệm
 Chọn B
 du dx  Tính tích phân:
 u x 2 
  Đặt 2x 1 2x (chọn C 0 )
 dv e dx v e
 2
 1 1 
 1 1 5 3e2
 I (x 2) e2x e2xdx .
 2 0 2 0 4
 +Kiểm tra các đáp án:
Câu 3: Tích phân 3x 2 cos2 x dx bằng
 0
 3 3 1 1
 Ⓐ. 2 . Ⓑ. 2 . Ⓒ. 2 . Ⓓ. 2 .
 4 4 4 4 Lời giải PP nhanh trắc nghiệm
 Chọn B
  Tính tích phân: 
  Đặt I 3x 2 cos2 x dx . Ta có:
 0
 1 
 3x 2 1 cos 2x dx
 2 0 
 1 1
 3x 2 dx 3x 2 cos 2x dx I I .
 1 2 
 2 0 0 2
 3 3
 I 3x 2 dx x2 2x 2 2 .
 1 
 0 2 0 2 
 Kiểm tra các đáp án:
 I 3x 2 cos 2x dx . Dùng tích phân từng phần
 2 
 0
 du 3dx
 u 3x 2 
Đặt 1 .
 dv cos 2x dx v sin 2x
 2
Khi đó 
 1 3 
 I 3x 2 sin 2x sin 2x dx
 2 
 2 0 2 0
 3 
 0 cos 2x 0 .
 4 0
 1 3 2 3 2
Vậy I 2 
 2 2 4
B - Bài tập rèn luyện:
 1
Câu 1: Xét tích phân I (2x2 4)e2xdx Nếu đặt u 2x2 4, v ' e2x , ta được tích phân: 
 0
 1
 1
 I (x) 2xe2xdx , trong đó:
 0 
 0
 2 2x 2 2x 2 x
 Ⓐ. (x) (x 2)e . Ⓑ. (x) (2x 4)e . Ⓒ. (x) (x 2)e . Ⓓ. 
 1 2 x
 (x) (2x 4)e .
 2
 2
Câu 2: Tính tích phân I x cos xdx
 0
 1
 Ⓐ. I . Ⓑ. I 1. Ⓒ. I . Ⓓ. I .
 2 2 3 3 2
 1
Câu 3: Tính xexdx
 0
 1
 Ⓐ. e . Ⓑ. e 1. Ⓒ. 1. Ⓓ. e 1.
 2 
Câu 4: L x sin xdx
 0
 Ⓐ. L . Ⓑ. L 2 . Ⓒ. L 0 . Ⓓ. L .
Câu 5: x 2 cos 2xdx
 0
 1 1 1
 Ⓐ. 0 . Ⓑ. . Ⓒ. . Ⓓ. .
 4 4 2
 4
Câu 6: xcos2xdx bằng
 0
 2 1 
 Ⓐ. . Ⓑ. . Ⓒ. 3 . Ⓓ. 2 
 8 4 2 2
 1
Câu 7: Tính tích phân I (x 1)e3xdx
 0
 5 2 2 5 2 5 5 2
 Ⓐ. I e3 . Ⓑ. I e3. Ⓒ. I e3 . Ⓓ. I e3 .
 9 9 9 9 9 9 9 9
 1
Câu 8: Tính tích phân I xe1 xdx
 0
 Ⓐ. 1. Ⓑ. e 2. Ⓒ. 1 e. Ⓓ. 1.
 1
Câu 9: Tính tích phân I (x 1)e3xdx
 0
 5 2 2 5 2 5 5 2
 Ⓐ. I e3 . Ⓑ. I e3. Ⓒ. I e3 . Ⓓ. I e3 .
 9 9 9 9 9 9 9 9
 1
Câu 10: Tính tích phân I xe1 xdx
 0
 Ⓐ. 1. Ⓑ. e 2. Ⓒ. 1 e. Ⓓ. 1.
 BẢNG ĐÁP ÁN
 1.A 2.C 3.C 4.A 5.A 6.A 7.A 8.D 9.A 10.D  Dạng ②: Tích phân chứa đa thức và ln
 
 ②. Loại 2: f x ln ax b dx
 -Phương pháp: 
 1
 gu ln x gdu dx
 x
 .Đặt: 
 gdv P(x)dx v P(x)dx Q(x)
 g 
A - Bài tập minh họa: 
 e
Câu 1: Tích phân x ln xdx bằng
 1
 e2 1 e2 e2 1 1 e2
 Ⓐ. . Ⓑ. 1. Ⓒ. . Ⓓ. .
 4 4 4 4 2 4
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio: 
 e x2 e x x2 x2 e2 1
 x ln xdx ln x e dx ( ln x) e 
 1 1
 1 2 1 2 4 2 4
 5
Câu 2: Tính tích phân I x 1 ln x 3 dx ?
 4
 19 19 19
 Ⓐ. 10ln2. Ⓑ. 10ln 2 . Ⓒ. 10ln 2 . Ⓓ. 10ln 2 .
 4 4 4
 Lời giải PP nhanh trắc nghiệm
  Chọn D  Casio:
 1
 du dx
 u ln x 3 x 3
Đặt .
 dv x 1 1 2
 v x x
 2
 1 2
 5 x x
 1 2 5 2
 I x x ln x 3 dx  Kiểm tra các đáp án:
 2 4 4 x 3
 35 1 5 x2 9 9 5 x 3 3
 ln 2 dx dx
 2 2 4 x 3 4 x 3
 35 1 9 
 ln 2 3 9ln 2 1 3ln 2 
 2 2 2 
 19
 10ln 2 .
 4
 e
Câu 3: Tính x2 ln xdx
 1
 2e3 1 2e3 1 e3 2 e3 2
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 9 9 9 9
 Lời giải PP nhanh trắc nghiệm
 Chọn A
 1  Casio
 du dx
 u ln x 
 x
 2 
 dv x dx 1 3
 v x
 3
 e e e
 1 3 1 2 1 3 1 3
 I x ln x x dx e x
 3 1 3 1 3 9 1
 1 e3 1 2e3 1
 e3 
 3 9 9
B - Bài tập rèn luyện:
 e
Câu 1: Tính tích phân I (x 2)ln xdx
 1
 1 e2 2 e2 1 e2 1
 Ⓐ. I . Ⓑ. I . Ⓒ. I . Ⓓ. I . 
 2 2 4 4
 u ln x e
Câu 2. Nếu đặt thì tích phân I 2x 1 ln xdx trở thành
 dv 2x 1 dx 
 1
 e e
 e e
 Ⓐ. I x2 x x 1 dx . Ⓑ. I x2 ln x x 1 dx .
 1 1 
 1 1
 e e
 e e
 Ⓒ. I x2 ln x xdx . Ⓓ. I x2 x ln x x 1 dx .
 1 1 
 1 1
 0
Câu 3: Tính tích phân J x ln x 1 dx 
 0
 4 5 2 3
 Ⓐ. J ln 3. Ⓑ. J ln 3. Ⓒ. J ln 3. Ⓓ. J ln 3.
 3 3 3 4
 5
Câu 4: Tính tích phân I x 1 ln x 3 dx ?
 4
 19 19 19
 Ⓐ. 10ln2. Ⓑ. 10ln 2 . Ⓒ. 10ln 2 . Ⓓ. 10ln 2 
 4 4 4
 3
Câu 5: Tích Phân I ln(x2 x)dx là 
 2 Ⓐ. 3ln3 . Ⓑ. 2ln 2 . Ⓒ. 3ln3 2. Ⓓ. 2 3ln3.
 2 ln x
Câu 6: Tích phân I dx bằng
 2
 1 x
 1 1 1 1
 Ⓐ. 1 ln 2 . Ⓑ. 1 ln 2 . Ⓒ. ln 2 1 . Ⓓ. 1 ln 2 .
 2 2 2 4
 b
Câu 7: Cho a b 1. Tích phân I ln x 1 dx bằng biểu thức nào sau đây?
 a
 b b
 I x 1 ln x 1 a b . I x 1 ln x 1 b a .
 Ⓐ. a Ⓑ. a
 b
 b
 1 b x
 Ⓒ. I . Ⓓ. I x ln x 1 dx .
 x 1 a x 1
 a a
 BẢNG ĐÁP ÁN
 1.C 2.D 3.C 4.D 5.C 6.A 7B
  Dạng ③: Tích phân chứa từng phần chứa tham số a, b, c
 -Phương pháp: Tích phân từng phần.
  sin ax 
 ①. f x cos ax dx ②. f x ln ax b dx
 ax 
 e 
A - Bài tập minh họa: 
 e a.e2 b
Câu 1: Cho I x ln xdx với a , b , c ¢ . Tính T a b c .
 1 c
 Ⓐ. .5 Ⓑ. . 3 Ⓒ. . 4 Ⓓ. . 6
 Lời giải PP nhanh trắc nghiệm
  Casio
  Chọn D
 1
 du dx
 u ln x x
 Ta có: nên .
 dv xdx x2
 v + Thử C=1,2,3,4,5,6.. giải hệ tìm a,b nguyên.
 2
 e
 e x2 1 e e2 1
 I x ln xdx ln x xdx .
 1 2 1 2 1 4
 a 1
 b 1 .
 c 4
Vậy T a b c 6 .
B - Bài tập rèn luyện:
 e 3ea 1
Câu 1: Cho x3 ln xdx với a,b ¢ . Tổng a b bằng
 1 b
 Ⓐ. 20 . Ⓑ. 10. Ⓒ. 17 . Ⓓ. 12.
 2 ln x b
Câu 2: Biết dx= a ln 2 trong đó a ¡ ; b , c là các số nguyên dương và nguyên tố cùng nhau. 
 2
 1 x c
 Tính giá trị của 2a 3b c.
 Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 6.
 2 ln x b b
Câu 3: Cho tích phân I dx a ln 2 với a là số thực, b và c là các số dương, đồng thời là 
 2
 1 x c c
 phân số tối giản. Tính giá trị của biểu thức P 2a 3b c .
 Ⓐ. P 6 . Ⓑ. P 5 . Ⓒ. P 6 . Ⓓ. P 4 .
 2
Câu 4: Cho x 1 exdx ae2 be c với a , b , c là các số nguyên. Tính a b c .
 1
 Ⓐ. 3. Ⓑ. 4. Ⓒ. 1. Ⓓ. 0.
 e
Câu 5: Biết I x2 ln xdx ae3 b với a , b là các số hữu tỉ. Giá trị của 9 a b bằng
 1
 Ⓐ. 3 . Ⓑ. 10 . Ⓒ. 9 . Ⓓ. 6 .
 e
Câu 6: Biết I x2 ln xdx ae3 b với a , b là các số hữu tỉ. Giá trị của 9 a b bằng
 1
 Ⓐ. 3 . Ⓑ. 10 . Ⓒ. 9 . Ⓓ. 6 .
 2 ln x a a
Câu 7: Cho I dx ln 2 ln c với a, b, c là các số nguyên dương và là phân số tối giản. 
 x 1 2 b b
 1 
 a b
 Tính giá trị của biểu thức S .
 c
 5 8 6 10
 Ⓐ. S . Ⓑ. S . Ⓒ. S . Ⓓ. S .
 3 3 5 3
 2
Câu 8: Biết 2x ex exdx a.e4 b.e2 c với a,b,c là các số hữu tỉ. Giá trị của 2a 3b 2c bằng
 0
 Ⓐ. 9. Ⓑ. 10. Ⓒ. 8. Ⓓ. 7. 2 ln x b
Câu 9: Biết dx aln 2 . Giá trị của 2a 3b c bằng.
 2
 1 x c
 Ⓐ. 6 . Ⓑ. 4 . Ⓒ. 5 . Ⓓ. 6 .
 5
Câu 10. Cho ln x2 x dx a ln 5 bln 2 c với a , b , c là các số nguyên. Tính S a 2b c .
 2
 Ⓐ. S 23. Ⓑ. S 20. Ⓒ. S 17 . Ⓓ. S 11.
 BẢNG ĐÁP ÁN
 1.A 2.C 3.D 4.C 5.A 6.A 7.B 8.B 9.B 10.A
 Hướng dẫn giải
 1 x4
Câu 1: Đặt u ln x du dx ; dv x3dx v .
 x 4
 e
 4 e 4 e 4 4 4
 x 1 3 e 1 4 e e 1 3e 1
 I ln x. x dx x .
 4 4 4 16 4 16 16 16
 1 1 1
 a 4
 a b 20.
 b 16
Câu 2:
 1
 u ln x du = dx
 x
 Đặt 1 .
 dv = dx 1
 x2 v 
 x
 2 2
 2 ln x 1 2 1 1 1 1 1
 Ta có 2 dx= ln x 2 dx ln 2 ln 2 .
 x x x 2 x 2 2
 1 1 1 1
 1
 Theo đề ta có a , b 1, c 2 .
 2
 Do đó 2a 3b c 4.
Câu 3: 
 dx
 u ln x du 2
 x ln x 2 1 ln x 1 2 1 ln 2
 Đặt dx I 2 dx 
 dv 1 x 1 x x x 1 2 2
 x2 v 1
 x
 1
 b 1,c 2,a P 2a 3b c 4 .
 2
Câu 4: u x 1 x
 Đặt x ta được du dx,v e .
 dv e dx
 2 2
 x 1 exdx x 1 ex 2 exdx xex 2 2e2 e .
 1 1
 1 1
 a 2,b 1,c 0 a b c 1.
Câu 5: 
 1
 du dx
 u ln x x
 Đặt ta có 
 dv x2dx x3
 v 
 3
 e e
 x3 ln x e x2 e3 x3 2 1
 Suy ra I dx .e3 .
 3 1 1 3 3 9 1 9 9
 2 1
 Vậy a , b nên 9 a b 3.
 9 9
Câu 6: 
 1
 du dx
 u ln x x
 Đặt ta có 
 dv x2dx x3
 v 
 3
 e e
 x3 ln x e x2 e3 x3 2 1
 Suy ra I dx .e3 .
 3 1 1 3 3 9 1 9 9
 2 1
 Vậy a , b nên 9 a b 3.
 9 9
Câu 7: 
 Ta có:
 2 ln x 2 1 1 2 2 1 1 2 1 1 
 I dx ln xd ln x dx ln 2 dx
 2 
 1 x 1 1 x 1 x 1 1 1 (x 1)x 3 1 x x 1 
 a 5
 1 2 5 a b 8
 ln 2 ln x ln x 1 ln 2 ln 3 b 3 S .
 3 1 3 c 3
 c 3
Câu 8: