Chuyên đề Giải tích Lớp 12 - Chương 2: Lũy thừa. Mũ. Logarit - Bài 8: Bất phương trình logarit (Có đáp án)

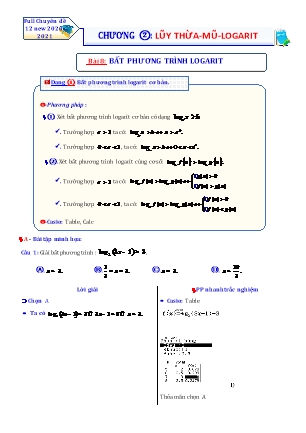
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ②: LŨY THỪA-MŨ-LOGARIT 
 Bài 8: BẤT PHƯƠNG TRÌNH LOGARIT
  Dạng ①: Bất phương trình logarit cơ bản.
 thức chứa lũy thừa.
 -Phương pháp: 
 ①. Xét bất phương trình logarit cơ bản có dạng loga x b.
 b
 . Trường hợp a 1 , ta có: loga x b x a .
 b
 . Trường hợp 0 a 1 , ta có: loga x b 0 x a .
 ②. Xét bất phương trình logarit cùng cơ số: loga f x loga g x .
 gg(x) 0
 . Trường hợp a 1 , ta có: loga f (x) loga g(x) 
 gf (x) g(x)
 gf (x) 0
 . Trường hợp 0 a 1 , ta có: loga f (x) loga g(x) 
 gf (x) g(x)
 -Casio: Table, Calc
A - Bài tập minh họa: 
Câu 1: Giải bất phương trình : log2 (3x - 1)> 3. 
 1 10
 Ⓐ. x > 3. Ⓑ. .
 3 3
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Casio: Table
  Ta có log (3x- 1)> 3 Û 3x- 1> 8 Û x > 3.
 2
 Thỏa mãn chọn A
 Câu 2: Tập nghiệm của bất phương trình log0,2 x 1 0 là
 Ⓐ. ;2 . Ⓑ. 2; . Ⓒ. ;1 . Ⓓ. 1;2 .
 Lời giải PP nhanh trắc nghiệm
 Chọn B  Casio: Calc, table
 0
 Ta có log0,2 x 1 0 x 1 0,2 x 2 .
 Vậy tập nghiệm của bất phương trình là 
 S 2; .
 2
Câu 3: Tập nghiệm của bất phương trình log 1 x 5x 7 0 là
 2
 Ⓐ. ;2  3; . Ⓑ. 3; . Ⓒ. ;2 . Ⓓ. 2;3 .
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio: Calc, table
 2 2
 log 1 x 5x 7 0 0 x 5x 7 1.
 2
 x2 5x 6 0
 2
 x 5x 7 0
 2 x 3.
Câu 4: Bất phương trình log3 3x 1 log3 x 7 có bao nhiêu nghiệm nguyên ? 
 Ⓐ. 2 . Ⓑ.3 . Ⓒ. 4 . Ⓓ. 1.
 Lời giải PP nhanh trắc nghiệm
 Chọn B  Casio: Calc, table
 Ta có:
 3x 1 x 7
 log3 3x 1 log3 x 7 
 3x 1 0
 x 3
 1
 1 x 3 .
 x 3
 3
 Vì x là số nguyên nên x 0;1;2 .
Vậy bất phương trình có 3 nghiệm nguyên.
B - Bài tập rèn luyện:
Câu 1: Tập nghiệm S của bất phương trình log x 1 là
 Ⓐ. S ;10 . Ⓑ. S 0;10 . Ⓒ. S ;1 . Ⓓ. S 10; . Câu 2: Tìm tập nghiệm S của bất phương trình log 1 x 0 .
 2
 1 1 
 Ⓐ. S ; . Ⓑ. S 1; . Ⓒ. S 0; . Ⓓ. S 0;1.
 2 2 
Câu 3: Tập nghiệm của bất phương trình log2 x 9 0 là
 Ⓐ. 9; . Ⓑ.10; . Ⓒ. 9; . Ⓓ. 10; .
Câu 4: Tập nghiệm của bất phương trình log2 x 1 4 là
 Ⓐ. ;17 . Ⓑ. ;17 . Ⓒ.1;17 . Ⓓ. 1;17 .
 1
Câu 5: Tập nghiệm của bất phương trình ln 0 là
 x
 Ⓐ. ( ;1) . Ⓑ. (0;1) . Ⓒ. (1; ) . Ⓓ. R .
Câu 6: Giải bất phương trình log 1 5x 3 2 , ta có nghiệm là
 5
 28 3 28 3 28 28
 Ⓐ. x . Ⓑ. x . Ⓒ. x . Ⓓ. x .
 5 5 5 5 5 5
 2
Câu 7: Bất phương trình log2 x 2x 3 1 có tập nghiệm là
 Ⓐ. ¡ \ 1 . Ⓑ. ¡ . Ⓒ. 1 . Ⓓ.  .
Câu 8: Tập nghiệm của bất phương trình 3 log2 x 4 là
 Ⓐ. 8;16 . Ⓑ. 0;16 . Ⓒ. 8; . Ⓓ. ¡ .
Câu 9: Tìm tập nghiệm S của bất phương trình log0,5 2x 1 2
 1 5 1 5 5 5 
 Ⓐ. S ; . Ⓑ. S ; . Ⓒ. S ; . Ⓓ. S ; .
 2 2 2 2 2 2 
 2
Câu 10: Tập nghiệm của bất phương trình log 1 x 1 là
 2
 Ⓐ. 2; . Ⓑ. 2;0  0; 2 .
 Ⓒ. 2; 2 . Ⓓ. 0; 2 .
 2
Câu 11: Tìm tập nghiệm của bất phương trình log 1 x 3x 2 1.
 2
 Ⓐ. ; 1 . Ⓑ.0; 1  2; 3. Ⓒ.0; 2  3; 7 . Ⓓ. 0; 2 .
 2
Câu 12: Bất phương trình log 2 2x x 1 0 có tập nghiệm là
 3
 3 3 
 Ⓐ. S 0; . Ⓑ. S 1; .
 2 2 
 1 3 
 Ⓒ. S ;0  ; . Ⓓ. S ;1  ; .
 2 2 
Câu 13:Tập nghiệm của bất phương trình: log1 x 3 1 0 có dạng a;b . Khi đó giá trị a 3b bằng
 3
 37
 Ⓐ. 15. Ⓑ.13. Ⓒ. . Ⓓ. 30 .
 3 Câu 14: Bất phương trình log2 x log3 x 1 có nghiệm là
 Ⓐ. x 3log2 6 . Ⓑ. x 2log3 6 . Ⓒ. x 6 . Ⓓ. x 3log6 2 .
 2
Câu 15: Cho hàm số f x log1 x 5x 7 . Nghiệm của bất phương trình f x 0 là
 3
 Ⓐ. x 3. Ⓑ. x 2 hoặc x 3. Ⓒ. 2 x 3 . Ⓓ. x 2 .
Câu 16: Tập nghiệm của bất phương trình: log0,4 (5x 2) log0,4 3x 6 là
 2 
 Ⓐ. ;2 . Ⓑ. 0;2 . Ⓒ. ;2 . Ⓓ. 2; .
 5 
Câu 17: Cho bất phương trình: log1 f x log1 g x . Khi đó bất phương trình tương đương:
 3 3
 Ⓐ. f x g x . Ⓑ. g x f x 0. Ⓒ. g x f x 0. Ⓓ. f x g x 
Câu 18: Nghiệm của bất phương trình log x 2 log 5 x là
 3 3 3 3
 Ⓐ. 2 x . Ⓑ. x 5 . Ⓒ. x . Ⓓ. x .
 2 2 2 2
Câu 19: Tập nghiệm của bất phương trình log2 3x 1 log2 x 1 là
 1 
 Ⓐ. ;1 . Ⓑ. ;1 . Ⓒ. 1; . Ⓓ. 0;1 .
 3 
Câu 20: Tập nghiệm của bất phương trình log2 7 x log 1 x 1 0 là
 2
 Ⓐ. S 1;4 . Ⓑ. S ;4. Ⓒ. S 4; . Ⓓ. S 4;7 .
 2
Câu 21: Tập nghiệm của bất phương trình log0,5 x x log0,5 2x 4 là
 Ⓐ. ; 4  1;2 . Ⓑ.Đáp án khác. Ⓒ. 4; 1 . Ⓓ. ; 4  1; .
Câu 22: Tập nghiệm của bất phương trình log1 x 1 log3 11 2x 0 là
 3
 11 
 Ⓐ. S 1;4 Ⓑ. S 1;4 Ⓒ. S ;4 Ⓓ. S 3; 
 2 
 2
Câu 23: Tập nghiệm của bất phương trình log2 x 4 log2 3x là
 Ⓐ. 2; 4. Ⓑ. 1;4. Ⓒ. 2;4. Ⓓ. ; 24; .
Câu 24: Giải bất phương trình log2 3x 2 log2 6 5x được tập nghiệm là a;b . Hãy tính tổng 
 S a b
 8 28 11 31
 Ⓐ. S . Ⓑ. S . Ⓒ. S . Ⓓ. S .
 3 15 5 6
Câu 25: Tập nghiệm của bất phương trình 2log2 x 1 log2 5 x 1.
 Ⓐ. 3;5. Ⓑ. 1;3. Ⓒ.1;3 . Ⓓ. 1;5 .
Câu 26: Tìm tập nghiệm S của bất phương trình log0,5 x 1 log0,5 2x 1 
 Ⓐ. S 0; . Ⓑ. S 1; . Ⓒ. S ;0 . Ⓓ. S ;1 .
Câu 27: Tập nghiệm S của bất phương trình log 1 x 3 log 1 4 là
 2 2 Ⓐ. S ;7. Ⓑ. S 3;7. Ⓒ. S 3;7. Ⓓ. S 7; 
 x2 1
Câu 28: Điều kiện xác định của bất phương trình ln 0 là
 x
 1 x 0 x 1
 Ⓐ. . Ⓑ. x 1. Ⓒ. x 0 . Ⓓ. .
 x 1 x 1
 2
Câu 29: Tìm tập nghiệm S của bất phương trình: log 1 2 .
 2 x 1
 Ⓐ. S 1;1 2 . Ⓑ. S 1; 9 . Ⓒ. S 1 2; . Ⓓ. S 9; .
 4x 6
Câu 30: Tập nghiệm của bất phương trình log 0 là
 3 x
 3 3 
 Ⓐ. S 2; . Ⓑ. S  2;0 . Ⓒ. S ;2. Ⓓ. S ¡ \ ;0 .
 2 2 
 BẢNG ĐÁP ÁN
 1.B 2.D 3.D 4.D 5.B 6.B 7.A 8.A 9.A 10.B
 11.B 12.C 13.B 14.D 15.C 16.C 17.C 18.A 19.B 20.D
 21 22.A 23.A 24.C 25.B 26.B 27.B 28.A 29.D 30.A
  Dạng ②: Bất phương trình logarit đặt ẩn phụ.
 thức chứa lũy thừa.
 -Phương pháp: 
 . Bất phương trình có dạng : m.log2 f x n.log f x p 0
 a a 
 .Đặt t log f x , f x 0 . Bất phương trình trở thành mt 2 nt p 0 .
 a 
 .Giải bất phương trình tìm t suy ra x thỏa ĐK 
 -Casio: Table, Calc
 phương trình tìm t suy 
A - Bài tập minh họa: 
 2
Câu 1: Tìm tập nghiệm S của bất phương trình log2 x 5log2 x 4 0.
 Ⓐ. S ( ;2] [16; ) . Ⓑ. S [2;16].
 Ⓒ. S (0;2] [16; ) . Ⓓ. S ( ;1] [4; ) .
 Lời giải PP nhanh trắc nghiệm
Chọn C Casio
Điều kiện: x 0 . 
Với điều kiện trên bất phương trình tương đương
 2 log2 x 1 0 x 2
 log2 x 5log2 x 4 0 .
 log2 x 4 x 16
 2
Câu 2: Tập nghiệm của phương trình log2 x- 3log2 x + 2 < 0 là khoảng (a;b). Giá trị biểu 
 thức a2 + b2 bằng
 Ⓐ. 16 . Ⓑ.5. Ⓒ. 20 . Ⓓ. 10 .
 Lời giải PP nhanh trắc nghiệm
 Chọn C  Casio: Table
 2
 log2 x- 3log2 x + 2 < 0 Û (log2 x- 1)(log2 x- 2)< 0
 
 Û 1< log2 x < 2 Û 2 < x < 4 Û x Î (2;4)
 ïì a = 2
 Vậy íï Þ a2 + b2 = 20
 îï b = 4
 2
Câu 3: Bất phương trình log0,5 x 6 5log0,5 x có tập nghiệm là
 1 1 1 1 
 Ⓐ. 2; 3 . Ⓑ. 1; . Ⓒ. ; . Ⓓ. ; .
 3 8 4 8 
 Lời giải PP nhanh trắc nghiệm
 Chọn C  Casio: Table 
  Điều kiện: x 0. 
 2 2
 Ta có: log0,5 x 6 5log0,5 x log0,5 x 5log0,5 x 6 0
 1 1
 2 log x 3 x .
 0,5 4 8
 1 1
 So điều kiện, ta được: x .
 8 4
B - Bài tập rèn luyện:
 2
Câu 1: Bất phương trình log0,2 x 5log0,2 x 6 có tập nghiệm là
 1 1 1 
 Ⓐ. S ; . Ⓑ. S 2;3 . Ⓒ. S 0; . Ⓓ. S 0;3 .
 125 25 25 
 2
Câu 2: Xác định tập nghiệm S của bất phương trình log2 x log2 2x 3 0
 1 
 Ⓐ. S 0;  2; . Ⓑ. S 2; .
 4 1 
 Ⓒ. S ;  2; . Ⓓ. S 1; .
 4 
 2 2
Câu 3: Bất phương trình log 1 x 3log 1 x 2 0 có tập nghiệm S a;b. Giá trị của a b bằng
 2 2
 Ⓐ. 16. Ⓑ.12. Ⓒ.8. Ⓓ. 4.
 2
Câu 4: Tập nghiệm của bất phương trình log2 x 4log2 x 3 0 là
 Ⓐ. 0;2  8; Ⓑ. ;2  8; Ⓒ. 2;8 Ⓓ. 8; 
 2
Câu 5: Nghiệm của bất phương trình log 1 x log2 2x 5 0 là
 2
 1 1 
 Ⓐ. x 0;  9; . Ⓑ. x 0; 8; .
 4 4 
 1 1 
 Ⓒ. x ; 8; . Ⓓ. x ; 9; .
 4 4 
 x3 32 
Câu 6: Nếu đặt t log x thì bất phương trình log4 x log2 9log 4log2 x trở thành 
 2 2 1 2 2 2 1 
 2 8 x 
 bất phương trình nào?
 Ⓐ. t 4 13t 2 36 0 . Ⓑ.t 4 5t 2 9 0. Ⓒ.t 4 13t 2 36 0 . Ⓓ. t 4 13t 2 36 0 .
 2
Câu 7: Tập nghiệm S của bất phương trình log3 x - 3log3 x + 2 £ 0 là
 Ⓐ. S 3;9 . Ⓑ. S 1;9. Ⓒ. S 0;9. Ⓓ. S 1;2 .
 x3 32 
Câu 8: Nghiệm nguyên lớn nhất của bất phương trình log4 x log2 9log 4log2 x là
 2 1 2 2 2 1 
 2 8 x 
 Ⓐ. x 7 . Ⓑ. x 8 . Ⓒ. x 4 . Ⓓ. x 1 .
 3
Câu 9: Tập nghiệm của bất phương trình log 125x .log x log2 x là
 x 25 2 5
 Ⓐ. S 1; 5 . Ⓑ. S 1; 5 . Ⓒ. S 5;1 . Ⓓ. S 5; 1 .
 2
Câu 10: Xác định tập nghiệm S của bất phương trình log2 x log2 2x 3 0
 1 
 Ⓐ. S 0;  2; . Ⓑ. S 2; .
 4 
 1 
 Ⓒ. S ;  2; . Ⓓ. S 1; .
 4 
 BẢNG ĐÁP ÁN
 1.A 2.A 3.C 4.A 5.B 6.C 7.A 8.A 9.A 10.A  Dạng ③: Bất PT logarit chứa tham số
 -Phương pháp: 
 . Sử dụng PP giải BPT logarit kết hợp công thức, tính chất của mũ, lũy thừa, logarit
 . Khai thác điều kiện bài toán
 . Xử lý bài toán và chọn giá trị m thỏa ĐK bài toán.
B - Bài tập Vận dụng Cao rèn luyện:
 x
Câu 1: Tìm tất cả các giá trị thực của tham số m để bất phương trình log2 (5 1) m có nghiệm x 1?
 Ⓐ. m 2 . Ⓑ. m 2 . Ⓒ. m 2 . Ⓓ. m 2 .
 2
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình log2 mx x 2 vô nghiệm?
 m 4
 Ⓐ. m 4 . Ⓑ. 4 m 4 . Ⓒ. . Ⓓ. m 4 .
 m 4
 2
Câu 3: Tìm tất cả giá trị thực của tham số m để bất phương trình log3 x 4x m 1 nghiệm đúng 
 với mọi x ¡ .?
 Ⓐ. m 7 . Ⓑ. m 7 . Ⓒ. m 4 . Ⓓ. 4 m 7 .
 2
Câu 4: Tìm tất cả giá trị thực của tham số m để bất phương trình log 1 mx x log 1 4 vô nghiệm?
 5 5
 m 4
 Ⓐ. 4 m 4 . Ⓑ. . Ⓒ. m 4 . Ⓓ. 4 m 4 .
 m 4
Câu 5: Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất 
 2 2
 phương trình log5 x 1 log5 x 4x m 1 (1) .
 Ⓐ. m  12;13 . Ⓑ. m 12;13 . Ⓒ. m  13;12 . Ⓓ. m  13; 12 .
 2 2
Câu 6: Tìm m để bất phương trình 1 log5 x 1 log5 mx 4x m thoã mãn với mọi x ¡ .
 Ⓐ. 1 m 0 . Ⓑ. 1 m 0 . Ⓒ. 2 m 3. Ⓓ. 2 m 3.
Câu 7: Số giá trị nguyên của tham số m sao cho bất phương trình: 
 2 2
 log5 log x 1 log mx 4x m nghiệm đúng với mọi x thuộc ¡ .
 Ⓐ. 0. Ⓑ.m ¢ và m 3 . Ⓒ.1. Ⓓ. 2.
 2
Câu 8: Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình log2 x mlog2 x m 0 nghiệm 
 đúng với mọi giá trị của x 0; .
 Ⓐ. Có 4 giá trị nguyên. Ⓑ.Có 5 giá trị nguyên.
 Ⓒ.Có 6 giá trị nguyên. Ⓓ. Có 7 giá trị nguyên.
 x x
Câu 9: Tìm tất cả các giá trị thực của tham số m để bất phương trình log2 (5 1).log2 (2.5 2) m có 
 nghiệm x 1? Ⓐ. m 6 . Ⓑ. m 6 . Ⓒ. m 6 . Ⓓ. m 6 .
Câu 10: Trong tất cả các cặp x; y thỏa mãn log 4x 4y 4 1. Tìm m để tồn tại duy nhất cặp 
 x2 y2 2 
 x; y sao cho x2 y2 2x 2y 2 m 0 .
 2
 Ⓐ. 10 2 . Ⓑ. 10 2 và 10 2 .
 2 2
 Ⓒ. 10 2 và 10 2 . Ⓓ. 10 2 .
Câu 11: Tất cả các giá trị thực của m để bất phương trình x x x 12 m.log 3 có nghiệm là
 5 4 x
 Ⓐ. m 2 3 . Ⓑ. m 2 3 . Ⓒ. m 12log3 5 . Ⓓ. 2 m 12log2 5 .
 BẢNG ĐÁP ÁN
 1.A 2.B 3.A 4.D 5.A 6.C 7.C 8.B 9.C 10.A 11.B
 Hướng dẫn giải
 x
Câu 1: Tìm tất cả các giá trị thực của tham số m để bất phương trình log2 (5 1) m có nghiệm x 1?
 Ⓐ. m 2 . Ⓑ. m 2 . Ⓒ. m 2 . Ⓓ. m 2 .
 Lời giải
 x x
  x 1 5 1 4 log2 5 1 2 m 2
 2
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình log2 mx x 2 vô nghiệm?
 m 4
 Ⓐ. m 4 . Ⓑ. 4 m 4 . Ⓒ. . Ⓓ. m 4 .
 m 4
 Lời giải
 2 2
  log2 mx x 2 x mx 4 0(*)
 Phương trình vô nghiệm 0 m2 16 0 4 m 4
 2
Câu 3: Tìm tất cả giá trị thực của tham số m để bất phương trình log3 x 4x m 1 nghiệm đúng 
 với mọi x ¡ .?
 Ⓐ. m 7 . Ⓑ. m 7 . Ⓒ. m 4 . Ⓓ. 4 m 7 .
 Lời giải
 2 2
  log3 x 4x m 1 x ¡ x 4x m 3 0 x ¡ 0 m 7
 2
Câu 4: Tìm tất cả giá trị thực của tham số m để bất phương trình log 1 mx x log 1 4 vô nghiệm?
 5 5
 m 4
 Ⓐ. 4 m 4 . Ⓑ. . Ⓒ. m 4 . Ⓓ. 4 m 4 .
 m 4
 Lời giải
 2 2 2
  log 1 mx x log 1 4 mx x 4 x mx 4 0
 5 5
 x2 mx 4 0 vô nghiệm x2 mx 4 0 x R 0 4 m 4
Câu 5: Tìm tất cả các giá trị thực của tham số m sao cho khoảng 2;3 thuộc tập nghiệm của bất 
 2 2
 phương trình log5 x 1 log5 x 4x m 1 (1) .
 Ⓐ. m  12;13 . Ⓑ. m 12;13 . Ⓒ. m  13;12 . Ⓓ. m  13; 12 . Lời giải
 x2 4x m
 x2 1 m x2 4x f (x)
  (1) 
 5 2
 2 m 4x 4x 5 g(x)
 x 4x m 0
 m Max f (x) 12 khi x 2
 2 x 3
 Hệ trên thỏa mãn x 2;3 12 m 13.
 m Min f (x) 13 khi x 2
 2 x 3
 2 2
Câu 6: Tìm m để bất phương trình 1 log5 x 1 log5 mx 4x m thoã mãn với mọi x ¡ .
 Ⓐ. 1 m 0 . Ⓑ. 1 m 0 . Ⓒ. 2 m 3. Ⓓ. 2 m 3.
 Lời giải
 2
 mx 4x m 0
 BPT thoã mãn với mọi x ¡ . x ¡ 
 2 2
 5 x 1 mx 4x m
 m 0
 m 0 
 m 2
 2 2 
 mx 4x m 0 16 4m 0 m 2
  x ¡ 2 m 3.
 2 
 5 m x 4x 5 m 0 5 m 0 m 5
 2 
 16 4 5 m 0 m 3
 m 7
Câu 7: Số giá trị nguyên của tham số m sao cho bất phương trình: 
 log5 log x2 1 log mx2 4x m nghiệm đúng với mọi x thuộc ¡ .
 Ⓐ. 0. Ⓑ.m ¢ và m 3 . Ⓒ.1. Ⓓ. 2.
 Lời giải
 Bất phương trình xác định với mọi x thuộc ¡ khi:
 mx2 4x m 0,x ¡
 m 0 m 0
 m 2 1
 2 
 0 4 m 0
 Bất phương trình nghiệm đúng với mọi x thuộc ¡ khi:
 5x2 5 mx2 4x m, x ¡
 5 m x2 4x 5 m 0, x ¡
 5 m 0 m 5
 m 3 2
 2 
 0 m 10m 21 0
 Từ và ta được 2 m 3,m ¢ m 3 . Vậy có 1 giá trị m.
 2
Câu 8: Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình log2 x mlog2 x m 0 nghiệm 
 đúng với mọi giá trị của x 0; .
 Ⓐ. Có 4 giá trị nguyên. Ⓑ.Có 5 giá trị nguyên.
 Ⓒ.Có 6 giá trị nguyên. Ⓓ. Có 7 giá trị nguyên.
 Lời giải
 Đặt t log2 x x 0 
 Bất phương trình trở thành:t 2 mt m 0,t ¡ 0 m2 4m 0 4 m 0
 Vì m nguyên nên m 4; 3; 2; 1;0 . Vậy có 5 giá trị nguyên của m thỏa ycbt.