Chuyên đề Giải tích Lớp 12 - Chương 2: Lũy thừa. Mũ. Logarit - Bài 6: Phương trình logarit (Có đáp án)

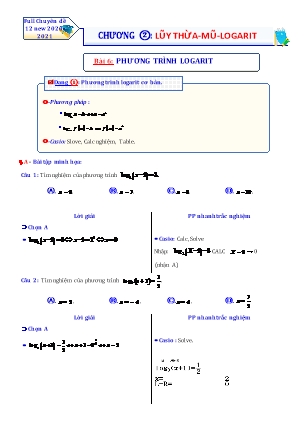
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ②: LŨY THỪA-MŨ-LOGARIT 
 Bài 6: PHƯƠNG TRÌNH LOGARIT
  Dạng ①: Phương trình logarit cơ bản.
 thức chứa lũy thừa.
 -Phương pháp: 
  log x b x ab
 a 
  log f x b f x ab
 a 
 -Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa: 
Câu 1: Tìm nghiệm của phương trình log2 x 1 3.
 Ⓐ. .x 9 Ⓑ. . x 7 Ⓒ.. x Ⓓ.8 . x 10
 Lời giải PP nhanh trắc nghiệm
 Chọn A
 3  Casio: Calc, Solve
  log2 x 1 3 x 1 2 x 9
 Nhập: log2 X 1 3 CALC X 9 0
 (nhận A)
 1
Câu 2: Tìm nghiệm của phương trình log (x + 1)= .
 9 2
 7
 Ⓐ. .x = 2 Ⓑ. . x = -Ⓒ.4 . Ⓓ.x = 4 x =
 2
 Lời giải PP nhanh trắc nghiệm
 Chọn A
 1 1  Casio : Solve.
  log x 1 x 1 92 x 2
 9 2
 2
Câu 3: Phương trình log3 (x 4x 12) 2 có tích hai nghiệm là 
 Ⓐ. 3 Ⓑ. 3 C. 4 Ⓓ. 4 
 Lời giải PP nhanh trắc nghiệm
 Chọn B
 2 2 2
 log3 (x 4x 12) 2 x 4x 12 3  Casio: table, Solve
  
 2 x 1
 x 4x 3 0 
 x 3
B - Bài tập rèn luyện:
 1
Câu 1: Tìm nghiệm của phương trình log (x + 1)= .
 9 2
 7
 Ⓐ. x = 2 . Ⓑ. x = - 4. Ⓒ. x = 4 . Ⓓ. x = .
 2
Câu 2: Giải phương trình log3 x 1 2 .
 Ⓐ. x 10 . Ⓑ. x 11. Ⓒ. x 8 . Ⓓ. x 7 .
Câu 3: Tìm tập nghiệm S của phương trình log4 x 3.
 Ⓐ. S 12. Ⓑ. S  . Ⓒ. S 64. Ⓓ. S 81 .
Câu 4: Nghiệm của phương trình log3 2x 1 2 là
 7 9
 Ⓐ. x 4 . Ⓑ. x . Ⓒ. x . Ⓓ. x 5 .
 2 2
 2
Câu 5: Tìm tập nghiệm của phương trình log3 2x x 3 1.
 1  1  1 
 Ⓐ. 0; . Ⓑ. 0 . Ⓒ. . Ⓓ. 0;  .
 2 2 2
Câu 6: Tìm nghiệm phương trình log3 2x 1 3 .
 Ⓐ. 4 . Ⓑ. 0 . Ⓒ.13. Ⓓ. 12.
Câu 7: Nghiệm của phương trình log4 x 1 3 là Ⓐ. x 80. Ⓑ. x 82. Ⓒ. x 65. Ⓓ. x 63.
 2
Câu 8: Tập nghiệm của phương trình log3 x 3x 3 1 là
 Ⓐ. 3. Ⓑ. 3;0. Ⓒ. 0;3. Ⓓ. 0.
Câu 9: Tập nghiệm của phương trình log(x2 x 4) 1 là
 Ⓐ. 3; 2. Ⓑ. 3. Ⓒ. 2. Ⓓ. 2;3 .
Câu 10: Tập nghiệm của phương trình ln(2x2 x 1) 0 là
 1  1 
 Ⓐ. 0 . Ⓑ. 0 ;  . Ⓒ.  . Ⓓ.  .
 2 2
 2
Câu 11: Số nghiệm của phương trình log2 x x 1 là
 Ⓐ. 0 . Ⓑ. 1 . Ⓒ. 2 . Ⓓ. 3.
 2
Câu 12: Gọi x1 , x2 là 2 nghiệm của phương trình log3 x x 5 log3 2x 5 . Khi đó x1 x2 bằng
 Ⓐ. 5 . Ⓑ. 3 . Ⓒ. 7 . Ⓓ. 2 .
Câu 13: Tìm số nghiệm của phương trình log3 2x 1 2.
 Ⓐ. 1. Ⓑ. 5. Ⓒ.2. Ⓓ. 0.
 2
Câu 14: Tập nghiệm của phương trình log1(x - 3x + 11) = - 2 là
 3
 Ⓐ. 1. Ⓑ. 1;2. Ⓒ. 1;2. Ⓓ. .
Câu 15: Nghiệm của phương trình log2 x 1 2 là
 Ⓐ. x 5 . Ⓑ. x 1. Ⓒ. x 4 . Ⓓ. x 3 .
 2
Câu 16: Giải phương trình log6 x 2 được kết quả là
 Ⓐ. x 36. Ⓑ. x 6. Ⓒ. x 6 . Ⓓ. x 6 .
Câu 17: Tìm nghiệm của phương trình: log x 4 3x 2
 Ⓐ. x 1. Ⓑ. x 4 . Ⓒ. x  . Ⓓ. x 1; 4.
Câu 18: Tìm x biết log5 x 3 2 .
 Ⓐ. x 1 . Ⓑ. x 28 . Ⓒ. x 13. Ⓓ. x 22 .
Câu 19: Phương trình log3 3x 2 3 có nghiệm là
 25 29 11
 Ⓐ. x . Ⓑ. x 87 . Ⓒ. x . Ⓓ. x .
 3 3 3
Câu 20: Nghiệm của phương trình log3 2x 3 2 là
 11 9
 Ⓐ. . Ⓑ. 6 . Ⓒ.5 . Ⓓ. .
 2 2
 BẢNG ĐÁP ÁN
 1.A 2.A 3.C 4.D 5.A 6.C 7.C 8.C 9.A 10.B
 11.C 12.C 13.A 14.B 15.A 16.B 17.C 18.B 19.C 20.B  Dạng ②: Phương trình logarit đưa về cùng cơ số
 -Phương pháp: 
  log f x log g x f x g x ,0 a 1; f x 0; hay g x 0
 a a 
 -Casio: Slove, Calc nghiệm, Table.
A - Bài tập minh họa: 
 2
Câu 1: Phương trình log3 5x 3 log1 x 1 0có 2 nghiệm x1 ; x2 trong đó x1 x2 . Giá trị của 
 3
 P 2x1 3x2 là
 Ⓐ. 13.Ⓑ. 14. Ⓒ. 3 . Ⓓ. 5 .
 Lời giải PP nhanh trắc nghiệm
 Chọn B
 2  Casio: Solve hoặc table
Phương trình tương đương với log3 5x 3 log3 x 1 
 x2 1 5x - 3 x 1
 , do x x nên x 1; x 4
 1 2 1 2
 5x 3 0 x 4
Suy ra P 2x1 3x2 2 12 14 .
Câu 2: Cho phương trình 2log x log 10 x log 9.log 2 . Hỏi phương trình đã cho có mấy 
 9 3 2 3
 nghiêm
 Ⓐ. 4 . Ⓑ. 3 . Ⓒ.1. Ⓓ. 2 .
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio: table_mode 8
Điều kiện 0 x 10
Ta có : 
 2 log9 x log3 10 x log2 9.log3 2 log3 x log3 10 x 2 1 tháa m·n
 2 x 
 log3 x 10 x 2 x 10x 9 0 
 x 9 tháa m·n 
. 
Vậy tập nghiệm của phương trình là S 1;9 .
Câu 3: Số nghiệm của phương trình log3 x.log3 (2x 1) 2log3 x
 Ⓐ. 2. Ⓑ. 0. Ⓒ.1. Ⓓ. 3.
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Casio: Solve hoặc table
 x 0 1
 Điều kiện: x .
 2x 1 0 2
  log3 x.log3 (2x 1) 2log3 x log3 x.(log3 (2x 1) 2) 0
 log3 x 0 x 1 x 1 TM 
 .
 log (2x 1) 2 2x 1 9
 3 x 5 TM 
 Vậy phương trình có 2 nghiệm.
B - Bài tập rèn luyện:
Câu 1: Tìm số nghiệm của phương trình ln 4x 2 ln x ln x 1 
 Ⓐ. .2 Ⓑ. . 0 Ⓒ.. 3 Ⓓ. . 1
Câu 2: Phương trình log3 (x 1) log3 3 log3 (4x 1) có nghiệm là
 Ⓐ. x 3 Ⓑ. x 3 Ⓒ. x 4 Ⓓ. x 2
Câu 3: Nghiệm của phương trình log2 x 1 1 log2 x 1 là
 Ⓐ. x 1. Ⓑ. x 2. Ⓒ. x 3 . Ⓓ. x 2 .
Câu 4: Với a , b , x là các số thực dương thỏa mãn log2 x 5log2 a 3log2 b. Mệnh đề nào dưới đây là 
 mệnh đề đúng? Ⓐ. x 3a 5b . Ⓑ. x a5 b3 . Ⓒ. x a5b3 . Ⓓ. x 5a 3b .
Câu 5: Tập nghiệm của phương trình log2021 x 1 log2021 2x 3 tương ứng là
 2
 Ⓐ. 4 . Ⓑ.  . Ⓒ. 4;  . Ⓓ. 2.
 3
 3
Câu 6: Số nghiệm thực của phương trình 3log3 (2x- 1)- log1 (x- 5) = 3 là
 3
 Ⓐ. 3 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 0 .
 3
Câu 7: Số nghiệm thực của phương trình 3log3 2x 1 log1 x 5 3 là
 3
 Ⓐ. 3. Ⓑ. 1 Ⓒ.2 Ⓓ. 0
 2
Câu 8: Phương trình log3 5x 3 log1 x 1 0có 2 nghiệm x1 ; x2 trong đó x1 x2 . Giá trị của 
 3
 P 2x1 3x2 là
 Ⓐ. 13. Ⓑ. 14. Ⓒ.3 . Ⓓ. 5 .
Câu 9: Cho phương trình 2log9 x log3 10 x log2 9.log3 2 . Hỏi phương trình đã cho có mấy 
 nghiêm
 Ⓐ. 4 . Ⓑ. 3 . Ⓒ.1. Ⓓ. 2 .
 3 2
Câu 10: Gọi P là tích tất cả các nghiệm của phương trình: log2 x x 1 log2 2x 1 . Tính P .
 Ⓐ. P 1. Ⓑ. P 3. Ⓒ. P 6 . Ⓓ. P 0 .
Câu 11: Số nghiệm của phương trình log3 x.log3 (2x 1) 2log3 x
 Ⓐ. 2. Ⓑ. 0. Ⓒ.1. Ⓓ. 3.
 2
Câu 12: Biết phương trình log2 x 5x 1 log4 9 có hai nghiệm thực x1 , x2 . Tích x1.x2 bằng
 Ⓐ. 8 . Ⓑ. 2 . Ⓒ.1. Ⓓ. 5 .
 2
Câu 13: Tổng các nghiệm của phương trình log4 x log2 3 1 là
 Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 0 .
Câu 14: Phương trình log x2 log 7 có tập nghiệm là
 4 2
 Ⓐ.  . Ⓑ. 7 . Ⓒ. 7. Ⓓ. 7; 7.
 log x 1 2 2 log 4 x log 4 x 3
Câu 15: Cho phương trình 4 2 8 . Tổng các nghiệm của phương 
 trình trên là
 Ⓐ. 4 2 6 . Ⓑ. 4 . Ⓒ. 4 2 6 . Ⓓ. 2 2 3 .
 4 2 2.
 log x.log x 8
Câu 16: Tổng các nghiệm của phương trình 3 3 bằng
 6562 82
 Ⓐ. 82. Ⓑ. . Ⓒ. . Ⓓ. 0.
 81 9
 2
Câu 17: Tổng các nghiệm của phương trình log4 x log2 3 1 là: Ⓐ. 6 . Ⓑ. 5 . Ⓒ. 4 . Ⓓ. 0 .
 1
Câu 18: Số nghiệm của phương trình log(x 10) log x2 2 log 4 là
 2
 Ⓐ. 2 . Ⓑ. 1 . Ⓒ. 4 . Ⓓ. 3 .
Câu 19: Giải phương trình log3 x 3 log1 x 5 1
 3
 Ⓐ. S 2 . Ⓑ. S 2;6 . Ⓒ. S 6. Ⓓ. S  .
Câu 20: Số nghiệm của phương trình ln x + ln(3x- 2)= 0 là
 Ⓐ. 0 . Ⓑ. 1. Ⓒ. 2 . Ⓓ. 3 .
 BẢNG ĐÁP ÁN
 1.D 2.D 3.C 4.C 5.B 6.B 7.B 8.B 9.D 10.D
 11.A 12.B 13 14.D 15.C 16.C 17.D 18.A 19.C 20.B
  Dạng ③: Đặt ẩn phụ
 -Phương pháp: 
 2
 . Dạng: A.loga f x B.loga f x C 0
  Đặt t loga f x , f x 0 . 
  Khi đó, phương trình trở thành : A.t 2 B.t C 0 . 
  Giải phương trình tìm t , thay t vào cách đặt để tìm x thỏa ĐK.
 1
 Chú ý : Nếu đặt t log f x thì log2 f x t 2 , log f x t, log f x t,....
 a a 1 a2 
 a 2
A - Bài tập minh họa: 
 2
Câu 1: Tích tất cả các nghiệm của phương trình log3 x 2log3 x 7 0 là
 Ⓐ. 9 Ⓑ. 7 Ⓒ..1 Ⓓ. 2
 Lời giải PP nhanh trắc nghiệm
  Chọn A  Công thức nhanh:
  2
 Điều kiện : x 0 . Nếu A.loga x B.loga x C 0 có hai nghiệm phân 
 B
  Đặt t log3 x . Khi đó pt trở thành : A
 biệt x1; x2 thì x1x2 a
 t 1 2 2  Casio:
 t 2 2t 7 0 
 t 1 2 2
 log x 1 2 2 x 31 2 2 (n)
Với 3 1
 1 2 2 
 log3 x 1 2 2 x2 3 (n)
 x1.x2 9 
 2 2
Câu 2: Số nghiệm của phương trình log2 x 8log2 x 4 0 là
 Ⓐ. x 2 . Ⓑ. x 3 . Ⓒ. x 1. Ⓓ. x 0 .
 Lời giải PP nhanh trắc nghiệm
 Chọn D
  Điều kiện : x 0 .  Casio: table
 2 2
 log2 x 8log2 x 4 0
 2
 2log2 x 8log2 x 4 0
 2
 4 log2 x 8log2 x 4 0
Đặt t log2 x . Khi đó pt trở thành : 
 4t 2 8t 4 0 t 1 
 1
 log x 1 x n .
 2 2
 2 2 2
Câu 3: Gọi x1; x2 là hai nghiệm của phương trình log3 x 3log3 x 2 0 .Giá trị biểu thức P x1 x 2 
bằng bao nhiêu ?
 Ⓐ. x 20 . Ⓑ. x 92 . Ⓒ. x 90 . Ⓓ. x 9 .
 Lời giải PP nhanh trắc nghiệm
 Chọn C
  Điều kiện : x 0 . Casio: Solve
 Đặt t log3 x . Khi đó pt trở thành : 
 t 1 log3 x 1 x 3 n 
 t 2 3t 2 0 
 t 2 log x 2
 3 x 9 n 
 2 2 2 2
 P x1 x2 3 9 90. B - Bài tập rèn luyện:
 2 2
Câu 1: Cho phương trình log 2 x 5 log 2 x 2 0 . Bằng cách đặt t log2 x phương trình trở thành 
 phương trình nào dưới đây?
 Ⓐ. 2t 2 5t 1 0 . Ⓑ. t 4 5t 1 0 .
 Ⓒ. 4t 2 5t 1 0 . Ⓓ. 2t 4 5t 1 0 .
 2
Câu 2: Phương trình log2 x 5log2 x 4 0 có hai nghiệm x1 , x2 . Khi đó tích x1.x2 bằng
 Ⓐ. 36. Ⓑ. 64. Ⓒ.32. Ⓓ. 16.
 2
Câu 3: Tích tất cả các nghiệm của phương trình log3 x 2log3 x 7 0 là
 Ⓐ. 9 . Ⓑ. 7 . Ⓒ.1 . Ⓓ. 2 .
 tổng các nghiệm bằng 0.
 2 2
Câu 4: Số nghiệm của phương trình log2 x 8log2 x 4 0 là
 Ⓐ. 2 . Ⓑ. 3 . Ⓒ.0 . Ⓓ. 1.
 2
Câu 5: Tích tất cả các nghiệm của phương trình log3 x- 2log3 x- 7 = 0 là
 Ⓐ. 9 . Ⓑ. - 7 . Ⓒ.1. Ⓓ. 2 .
 17
Câu 6: Tích tất cả các nghiệm của phương trình log 2 x log x bằng
 2 2 4
 3 17 1 1
 Ⓐ. . Ⓑ. . Ⓒ. . Ⓓ. .
 2 4 4 2
 2 2
Câu 7: Số nghiệm của phương trình log2 x + 8log2 x + 4 = 0 là
 Ⓐ. 2 . Ⓑ. 3 . Ⓒ. 0 . Ⓓ. 1.
 x
Câu 8: Tích tất cả các nghiệm của phương trình log2 12 2 5 x bằng
 Ⓐ. 2. Ⓑ. 1. Ⓒ.6 . Ⓓ. 3 .
 x
Câu 9: Tập nghiệm của phương trình: log3 (9 8) x 2 là
 Ⓐ. 0. Ⓑ. 1;8. Ⓒ. 0;log3 4. Ⓓ. 0;log3 8.
 2
Câu 10: Phương trình log2 x 3log1 x 2 0 có tổng tất cả các nghiệm là
 2
 Ⓐ. 6 . Ⓑ. 8 . Ⓒ.9 . Ⓓ. 5 .
 2
Câu 11: Tổng tất cả các nghiệm của phương trình log3 x- 4log2 x.log3 2+ 3 = 0 bằng
 Ⓐ. 81. Ⓑ. 9 . Ⓒ.30. Ⓓ. 4 .
 2
Câu 12: Tổng các nghiệm của phương trình 4log4 x 1 3log2 x 1 2 0 là
 Ⓐ. 8 . Ⓑ. 3 . Ⓒ. 2. Ⓓ. 15. 2
Câu 13: Gọi x1 , x2 là các nghiệm của phương trình log2 x 3log2 x 2 0 . Giá trị của biểu thức 
 2 2
 P x1 x2 bằng bao nhiêu?
 Ⓐ. 20. Ⓑ. 5. Ⓒ.36. Ⓓ. 25.
 x x a b
Câu 14: Biết nghiệm lớn nhất của phương trình log2 4 2 2 x 2 có dạng x log2 với 
 c
 a,b,c là số nguyên tố. Tính P a b c .
 Ⓐ. 23. Ⓑ. 24. Ⓒ.25. Ⓓ. 26.
 2
Câu 15: Biết phương trình ln x ln x 12 0 có hai nghiệm phân biệt x1 và x2 . Tính tích x1x2 .
 1 1 1
 Ⓐ. x x Ⓑ. x x . Ⓒ. x x . Ⓓ. x x e3 .
 1 2 e4 1 2 e12 1 2 e 1 2
 2 2 3
Câu 16: P là tích các nghiệm của phương trình log2 x 4log2 x 8 0 , giá trị của P là
 Ⓐ. P 8 . Ⓑ. P 6 . Ⓒ. P 64 . Ⓓ. P 4 .
 Lời giải
 x
Câu 17: Tổng tất cả các nghiệm của phương trình log 3 7 3 2 x bằng
 Ⓐ. 2. Ⓑ. 1. Ⓒ.7 . Ⓓ. 3.
 2
Câu 18: Phương trình log2 x 3log 1 x 2 0 có tổng tất cả các nghiệm là
 2
 Ⓐ. 6 . Ⓑ. 8 . Ⓒ.9 . Ⓓ. 5 .
 2
Câu 19: Gọi x1 , x2 là các nghiệm của phương trình log2 x 3log2 x 2 0 . Giá trị của biểu thức 
 2 2
 P x1 x2 bằng bao nhiêu?
 Ⓐ. 20. Ⓑ. 5. Ⓒ.36. Ⓓ. 25.
 2
Câu 20: Phương trình log2 x log2 8x 3 0 tương đương với phương trình nào sau đây?
 2 2
 Ⓐ. log2 x log2 x 0 . Ⓑ. log2 x log2 x 6 0 .
 2 2
 Ⓒ. log2 x log2 x 0 . Ⓓ. log2 x log2 x 6 0
 BẢNG ĐÁP ÁN
 1.C 2.C 3.A 4.D 5.A 6.D 7.D 8.C 9.D 10.A
 11.C 12.A 13.A 14.B 15.C 16.A 17.A 18.A 19.A 20.C
  Dạng ⑤: PT chứa tham số m 
 -Phương pháp: 
 . Sử dụng các phương phá giải PT logarit và các kiến thức có liên quan để tìm tham số 
 m
  .Casio: Table, Solve
 Bài tập vận dụng rèn luyện: