Chuyên đề Giải tích Lớp 12 - Chương 2: Lũy thừa. Mũ. Logarit - Bài 3: Logarit (Có đáp án)

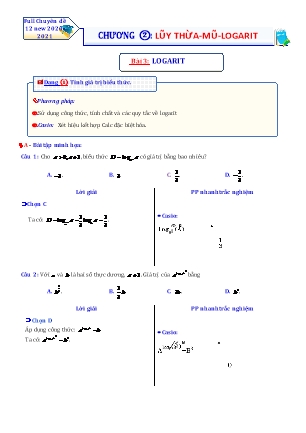
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ②: LŨY THỪA-MŨ-LOGARIT 
 Bài 3: LOGARIT
  Dạng ①: Tính giá trị biểu thức. 
 thức chứa lũy thừa.
 Phương pháp: 
 .Sử dụng công thức, tính chất và các quy tắc về logarit
 .Casio: Xét hiệu kết hợp Calc đặc biệt hóa.
A - Bài tập minh họa: 
Câu 1: Cho a 0,a 1, biểu thức D log a có giá trị bằng bao nhiêu?
 a3
 1 1
 A. 3 . B. 3.C. . D. .
 3 3
 Lời giải PP nhanh trắc nghiệm
 Chọn C
 1 1  Casio: 
 Ta có: D log a log a .
 a3 3 a 3
 3
Câu 2: Với a và b là hai số thực dương, a 1. Giá trị của aloga b bằng
 1 1
 A. b3 . B. b . C. 3b . D. b3 .
 3
 Lời giải PP nhanh trắc nghiệm
 Chọn D
 loga b
 Áp dụng công thức: a b  Casio: 
 3
 Ta có: aloga b b3 .
 Câu 3: Cho hai số thực dương a, b và a 1. Khẳng định nào đúng ?
 1
A. log ab log b .B. 2021log ab 1 log b2021 .
 a 2 a a a
 2020 2018
C. loga a b 2020 loga b . D. loga a b 2018 1 loga b .
 Lời giải PP nhanh trắc nghiệm
 Chọn C.
 log ab 2 log a log b  Casio: 
 a a a 
  
 2 2loga b.
 2018
  2018loga ab 2018 loga b 
 2020
 loga a b 2020.loga a loga b
   Chú ý: 2020 ta chọn số 2 đại diện là OK
 2020 loga b
B - Bài tập rèn luyện:
Câu 1: Với a là số thực dương tùy ý. Chọn khẳng định đúng
 1 1
 Ⓐ. log a3 3 log a. Ⓑ. log a3 3.log a. Ⓒ. log a3 log a. Ⓓ. log a3 log a.
 2 2 2 2 2 3 2 2 3 2
 a3 
Câu 2: Cho a là số thực dương khác 4 . Tính I log a .
 4 64 
 1 1
 Ⓐ. I .Ⓑ. I 3 .Ⓒ. I 3 .Ⓓ. I .
 3 3
Câu 3: Cho 2 số thực a và b với a 0,a 1,b 0 . Khẳng định nào sau đây là sai?
 1 1 2 1 2 1 2
 Ⓐ. log 2 b log b .Ⓑ. log a 1.Ⓒ. log b log b .Ⓓ. log b log b .
 a 2 a 2 a 2 a a 2 a a
 a2 3 a2 5 a4 
Câu 4: Tính log .
 a 15 7 
 a 
 a2 3 a2 5 a4 a2 3 a2 5 a4 12
 Ⓐ. log 3 .Ⓑ. log .
 a 15 7 a 15 7 
 a a 5
 a2 3 a2 5 a4 9 a2 3 a2 5 a4 
 Ⓒ. log .Ⓓ. log 2.
 a 15 7 a 15 7 
 a 5 a 
 a b c d
Câu 5: Cho các số thực dương a,b,c,d và biểu thức: M lg lg lg lg . Khẳng định nào sau 
 b c d a
 đây đúng?
 Ⓐ. M 1.Ⓑ. M 0 . a b c d 
 Ⓒ. M lg abcd .Ⓓ. M lg .
 b c d a 
Câu 6: Biểu thức log2 2sin log2 cos có giá trị bằng:
 12 12 
 Ⓐ. 1.Ⓑ. 2 .Ⓒ. 1.Ⓓ. log2 3 1.
 log 4 3loga 4
Câu 7: Tính giá trị của biểu thức P a a a , với a 0,a 1 .
 Ⓐ. P 24 .Ⓑ. P 8 .Ⓒ. P 8 .Ⓓ. P 12.
 2 4
Câu 8: Nếu loga b p thì loga a b bằng
 Ⓐ. 4 p 2.Ⓑ. 4 p 2a .Ⓒ. a2 p4 .Ⓓ. p4 2a .
Câu 9: Cho các số thực a,b,c thỏa mãn: alog3 7 27,blog7 11 49,clog11 25 11 . Giá trị của biểu thức 
 2 (log 25)2
 2 (log711) 11
 A a(log3 7) b c là
 Ⓐ. A 519.Ⓑ. A 729 .Ⓒ. A 469 .Ⓓ. A 129.
 a 
 P log a10b2 log log b 2 0 a 1;0 b 1
Câu 10: Tính giá trị của biểu thức a2 a 3 b ( với ).
 b 
 Ⓐ. P 2 .Ⓑ. P 1.Ⓒ. P 3 .Ⓓ. P 2 .
Câu 11: Giá trị của biểu thức M log2 2 log2 4 log2 8 ... log2 256 bằng
 Ⓐ. 56 .Ⓑ. 8.log2 256 .Ⓒ. 48 .Ⓓ. 36 .
 p
Câu 12: Giả sử p, q là các số thực dương sao cho log p log q log p q . Tìm giá trị của .
 9 12 16 q
 1 1 4 8
 Ⓐ. 1 5 .Ⓑ. 1 5 .Ⓒ. .Ⓓ. .
 2 2 3 5
Câu 13: Cho a, b là các số thực dương khác 1, thoả log b log a 1. Mệnh đề nào dưới đây là đúng?
 a2 b2
 1 1
 Ⓐ. a .Ⓑ. a b .Ⓒ. a .Ⓓ. a b2 .
 b b2
 a
Câu 14: Cho a, b là các số thực dương và ab 1 thỏa mãn log a2 3 thì giá trị của log 3 bằng
 ab ab b
 3 3 8 2
 Ⓐ. .Ⓑ. .Ⓒ. .Ⓓ. .
 8 2 3 3
Câu 15: Cho a 0 , b 0 thỏa mãn a2 4b2 5ab . Khẳng định nào sau đây đúng? a 2b log a logb
 Ⓐ. log .Ⓑ. 5log a 2b log a logb .
 3 2
 Ⓒ. 2log a 2b 5 loga logb .Ⓓ. log a 1 logb 1.
Câu 16: Cho a , b là hai số thực dương, khác 1. Đặt loga b m , tính theo m giá trị của 
 P log b log a3.
 a2 b
 4m2 3 m2 12 m2 12 m2 3
 Ⓐ. P .Ⓑ. P .Ⓒ. P .Ⓓ. P .
 2m 2m m 2m
Câu 17: Cho P logm 16m và a log2 m với m là số dương khác 1.Mệnh đề nào dưới đây đúng?
 4 a 3 a
 Ⓐ. P 3 a2 .Ⓑ. P ..Ⓒ. P .Ⓓ. P 3 a. a .
 a a
Câu 18: Rút gọn biểu thức A loga b logb a 2 loga b logab b logb a 1 ta được kết quả là
 1 log a
 Ⓐ. Ⓑ. log a .Ⓒ. log a .Ⓓ. b
 . b b
 logb a 3 .
Câu 19: Kết quả rút gọn của biểu thức C loga b logb a 2 loga b logab b loga b là
 3
 3
 Ⓐ. loga b .Ⓑ. . loga b .Ⓒ. loga b .Ⓓ. loga b .
Câu 20: Cho a, b là các số thực dương thoả mãn a2 b2 14ab . Khẳng định nào sau đây là sai?
 a b ln a ln b
 Ⓐ. ln .Ⓑ. 2log a b 4 log a log b .
 4 2 2 2 2
 a b
 Ⓒ. 2log a b 4 log a log b .Ⓓ. 2log log a logb .
 4 4 4 4
 BẢNG ĐÁP ÁN
 1.B 2.C 3.D 4.A 5.B 6.A 7.C 8.A 9.C 10.B
 11.D 12.B 13.B 14.D 15.A 16.B 17.B 18.A 19.C 20.C
  Dạng ②: Biến đổi, rút gọn, biểu diễn biểu thức chứa logarit, mũ, lũy thừa.
 . Phương pháp: áp dụng các tính chất, quy tắc tính logarit, đổi cơ số
 . Casio: Xét hiệu kết hợp Calc đặc biệt hóa; Sto, Alpha khi biểu diễn
A - Bài tập minh họa: 
 Câu 1: Cho a 0;a 1. Tìm mệnh đề đúng trong các mệnh đề sau?
 n
 A. loga x nloga x . B. loga x có nghĩa x ¡ .
 C. loga a 0. D. loga x.y loga x.loga y;x 0 .
 Lời giải PP nhanh trắc nghiệm
 Chọn A
  loga x có nghĩa x 0 câu B sai  Casio: Xét hiệu với Calc đặc biệt hóa.
  loga a 1 câu C sai.
  loga x.y loga x loga y;x 0 câu D sai.
 Calc A=2, x=5, m=3 
 Chọn A
Câu 2: Cho a là số thực dương bất kì. Tìm khẳng định đúng trong các khẳng định sau:
 1
 A. log a3 log a . B. log 3a 3log a .
 3
 1
 C. log 3a log a . D. log a3 3log a .
 3
 Lời giải PP nhanh trắc nghiệm
Chọn D
  log a3 3log a A sai, D đúng.  Casio: Xét hiệu với Calc đặc biệt hóa.
  log 3a log3 loga B, C sai.
  Calc A=2
 Chọn D
Câu 3: Cho a là số thực dương khác 1. Tính I log a .
 a
 1
 A. I . B. I 2 . C. I 0 . D. I 2 .
 2 Lời giải PP nhanh trắc nghiệm
 Chọn D
  I log a 2log a 2  Casio: 
 Ta có: a a . 
 3
 a,b 0 a 1 P log 2 b
Câu 4: Cho , thỏa loga b 3 . Tính a .
 9 1
 A. P 18. B. P 2 .C. P . D. P .
 2 2
 Lời giải PP nhanh trắc nghiệm
 Chọn C
 3 3 9  Casio: 
 Vì a,b 0 nên ta có: P log b .3 .
 2 a 2 2
 Chọn A=2, tìm B=8.
B - Bài tập rèn luyện:
Câu 1: Cho b là số thực dương tùy ý, log b bằng
 32
 1 1
 Ⓐ. 2log b .Ⓑ. log b .Ⓒ. 2log b .Ⓓ. log b .
 3 2 3 3 2 3
Câu 2: Với a là số thực dương bất kỳ, khẳng định nào dưới đây đúng?
 1 1
 Ⓐ. log 4a 4 log a .Ⓑ. log a4 4 log a .Ⓒ. log a4 log a .Ⓓ. log 4a log a .
 4 4
Câu 3: Với a , b là hai số thực khác 0 tùy ý, ln a2b4 bằng
 Ⓐ. 2ln a 4ln b .Ⓑ. 4 ln a ln b .Ⓒ. 2ln a 4ln b .Ⓓ. 4ln a 2ln b .
Câu 4: Với a là một số thực dương bất kì, mệnh đề nào dưới đây đúng?
 Ⓐ. log(3a) 0. Ⓑ. log(3a) 3log a. 3 3
 Ⓒ. log2018 a 3log2018 a. Ⓓ. log a 0.
Câu 5: Với các số thực a,b,c 0 và a,b 1 bất kì. Mệnh đề nào dưới đây Sai?
 1
 Ⓐ. loga b .Ⓑ. loga b.c loga b loga c .
 logb a
 Ⓒ. log b.log c log c .Ⓓ. log c b c log b .
 a b a a a
Câu 6: Với số dương a tùy ý, ta có log 8a log 2a bằng
 Ⓐ. 6log a. Ⓑ. log 16a2 . Ⓒ. log 6a . Ⓓ. log 4.
Câu 7: Cho a > 0; b > 0. Tìm đẳng thức sai.
 2
 Ⓐ. log2(ab) 2log2(ab) .Ⓑ. log2 a log2 b log2 ab .
 a
 Ⓒ. log a log b log .Ⓓ. lo g a lo g b lo g ( a b ) .
 2 2 2 b 2 2 2
Câu 8: Với a,b> 0 tùy ý, mệnh đề nào dưới đây đúng?
 Ⓐ. log(ab)= log a.logb .Ⓑ. log(ab2 )= 2log a + 2logb .
 Ⓒ. log(ab2 )= log a + 2logb .Ⓓ. log(ab)= loga- logb.
Câu 9: Cho a , b là hai số thực dương tùy ý và b 1. Tìm kết luận đúng.
 Ⓐ. ln a ln b ln a b .Ⓑ. ln a b ln a.ln b .
 ln a
 Ⓒ. ln a lnb ln a b .Ⓓ. log a .
 b ln b
Câu 10: Với a là số thực dương bất kỳ, khẳng định nào sau đây đúng?
 Ⓐ. log(4a)= 4loga .Ⓑ. log(a4 )= 4log a .
 1 1
 Ⓒ. log(a4 )= log a .Ⓓ. log(4a)= log a .
 4 4
 3 6
Câu 11: Với a,b là các số thực dương tùy ý và a khác 1 , đặt P log b log 2 b . Mệnh đề nào dưới 
 a a
 đây đúng?
 Ⓐ. P 27 loga b .Ⓑ. P 15loga b .Ⓒ. P 9loga b .Ⓓ. P 6loga b .
Câu 12: Với a và b là hai số thực dương tùy ý, log a2b3 bằng.
 1 1 1
 Ⓐ. log a logb .Ⓑ. 2 log a logb .Ⓒ. log a logb .Ⓓ. 2log a 3logb .
 2 3 3
Câu 13: Cho ba số thực dương a,b,c với a ¹ 1 và Î ¡ . Mệnh đề nào sau đây sai?
 c
 Ⓐ. loga a = c .Ⓑ. loga (b- c) = loga b- loga c .
 Ⓒ. loga b = loga b .Ⓓ. loga a = 1.
Câu 14: Cho a 0;a 1; x, y là hai số thực dương. Đẳng thức nào sau đây là đúng?
 Ⓐ. loga xy loga x.loga y .Ⓑ. loga xy loga x loga y .
 Ⓒ. loga x y loga x loga y .Ⓓ. loga x y loga x.loga y Câu 15: Với a , b là hai số thực dương tuỳ ý, log a3b4 bằng
 Ⓐ. 2log a 3logb .Ⓑ. 3log a 4logb .
 1 1
 Ⓒ. 2 3loga 2logb .Ⓓ. log a logb .
 3 4
Câu 16: Với a , b là hai số thực tuỳ ý, log a2b4 bằng
 Ⓐ. 2log a 4logb .Ⓑ. 2log a 4logb .Ⓒ. 2log a 4log b .Ⓓ. 2log a 4log b .
Câu 17: Cho a 0;a 1; x, y là hai số thực dương. Đẳng thức nào sau đây là đúng?
 x 
 Ⓐ. loga xy loga x.loga y .Ⓑ. loga loga x loga y .
 y 
 Ⓒ. loga x y loga x loga y .Ⓓ. loga x y loga x.loga y
 125
Câu 18: Cho log 2 a . Tính log theo a được kết quả là
 4
 Ⓐ. 3 5a .Ⓑ. 4 1 a .Ⓒ. 6 7a .Ⓓ. 2 a 5 .
 log2 a b
Câu 19: Tính giá trị của biểu thức P 2 loga a a 0,a 1 .
 Ⓐ. P a b .Ⓑ. P 2a b .Ⓒ. P a b .Ⓓ. P 2a b .
Câu 20: Cho a là số thực dương bất kỳ. Mệnh đề nào dưới đây đúng?
 Ⓐ. log5 (5a)= 1+ log5 a .Ⓑ. log5 (5a)= 1+ a .
 Ⓒ. log5 (5a)= log5 a .Ⓓ. log5 (5a)= 5+ log5 a .
Câu 21: Cho các số thực a , b sao cho a b 0. Mệnh đề nào sau đây sai?
 a 2
 Ⓐ. log log a log b .Ⓑ. log a b 2log b a .
 b
 2
 Ⓒ. log a2b2 2 log a log b .Ⓓ. log a3b 4log a 2log ab .
Câu 22: Cho a là số thực dương tùy ý, mệnh đề nào sau đây đúng?
 Ⓐ. log2 8a 3 log2 a .Ⓑ. log2 8a 3 log2 a .
 Ⓒ. log2 8a 3log2 a .Ⓓ. log2 8a 8log2 a .
 log 3 a,log 5 b. I log 5
Câu 23: Biết 6 6 Tính 3 theo a,b.
 b b b b
 Ⓐ. I . Ⓑ. I . Ⓒ. I . Ⓓ. I .
 a 1 a 1 a a 1
Câu 24: Với a, b là hai số thực dương và a 1, log a b bằng
 a 
 1 1 1
 Ⓐ. 2 2log b .Ⓑ. 2 log b .Ⓒ. log b .Ⓓ. log b .
 a a 2 2 a 2 a
Câu 25: Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
 1
 Ⓐ. log 3a log a .Ⓑ. loga3 3log a .
 3 1
 Ⓒ. log 3a 3log a .Ⓓ. loga3 log a .
 3
Câu 26: Cho a,b là các số thực dương; a 1, là số thực bất kì. Mệnh đề nào sau đây đúng?
 2 2 2
 Ⓐ. log 2 b log b .Ⓑ. log b log b .
 a a a a
 Ⓒ. loga b loga b .Ⓓ. loga 2b 2loga b .
 a b c d
Câu 27: Cho các số thực dương a,b,c,d và biểu thức: M lg lg lg lg . Khẳng định nào sau 
 b c d a
 đây đúng?
 Ⓐ. M 1.Ⓑ. M 0 .
 a b c d 
 Ⓒ. M lg abcd .Ⓓ. M lg .
 b c d a 
Câu 28: Với a , b là hai số thực dương tuỳ ý, log ab2 bằng
 1
 Ⓐ. 2log a logb .Ⓑ. log a 2logb .Ⓒ. 2 log a logb .Ⓓ. log a logb .
 2
Câu 29: Cho log2 3 a . Hãy tính log4 54 theo a .
 1 1
 Ⓐ. log 54 1 3a .Ⓑ. log 54 1 6a .
 4 2 4 2
 1
 Ⓒ. log 54 1 12a .Ⓓ. log 54 2 1 6a .
 4 2 4
Câu 30: Cho biểu thức A log a2 log 4a với a 0, a 1.Khẳng định nào sau đây đúng?
 a 1
 2
 Ⓐ. A 1 2a .Ⓑ. A 4 2a .Ⓒ. A 1 2a .Ⓓ. A 4 2a .
 BẢNG ĐÁP ÁN
 1.B 2.B 3.A 4.C 5.D 6.D 7.D 8.C 9.D 10.B
 11.D 12.D 13.B 14.B 15.B 16.D 17.B 18.A 19.C 20.A
 21.A 22.B 23.A 24.B 25.B 26.C 27.B 28.B 29.A 30.D
  Dạng ③: Biểu diễn các biểu thức chứa logarit theo biểu thức khác
 -Phương pháp: 
 . Sử dụng công thức, tính chất của mũ, lũy thừa.
 . Casio: Xét hiệu với chức năng Calc sau khi Sto và Alpha vào các tham số a,b,c.
A - Bài tập minh họa: 
 a3 
 T log
Câu 1. Cho a,b,c 0,c 1 và đặt logc a m , logc b n , c . Tính T theo m,n .
 4 b3 
 3 3 3 3 3 3
 A. T m n . B. T 6n m . C. T m n . D. T 6m n .
 2 8 2 2 8 2
 Lời giải PP nhanh trắc nghiệm
ChọnD  Casio: Cho a 2,b 3,c 5.
 a3 3 Bấm log 2 0,4306765581lưu vào A
 T log log a3 log 4 b3 6log a log b 5
 c c c c c
 4 b3 2
 Bấm log5 3 0,6826061945lưu vào B
 3
 6m n
 2 23 
 log
 Bấm 5 trừ đáp án nếu bằng 0 
 4 33 
 thì nhận đáp án đó
 Lưu ý: m thay bởi A, n thay bởi B. 
Câu 2. Nếu log 4 a thì log 4000 bằng
 A. 3 a . B. 4 a . C. 3 2a. D. 4 2a .
 Lời giải PP nhanh trắc nghiệm
ChọnA  Casio: 
 Ta có 
 log 4000 log 4.103 log 4 log103 log 4 3 a 3.
 a log 15;b log 10. log 50
Câu 3. Đặt 3 3 Hãy biểu diễn 3 theo a và b.
 log 50 a b 1 log 50 3 a b 1
 A. 3 . B. 3 .
 log 50 2 a b 1 log 50 4 a b 1
 C. 3 . D. 3 
 Lời giải PP nhanh trắc nghiệm
Chọn C  Casio: 
 Ta có log 50 log 50 2log 50 2log 10.5
 3 1 3 3 
 32
 2 log3 10 log3 5 
 2 log3 10 log3 15 log3 3 
 2 a b 1