Chuyên đề Giải tích Lớp 12 - Chương 1: Đạo hàm. Ứng dụng - Bài 5: Đồ thị hàm số bậc ba (Có đáp án)

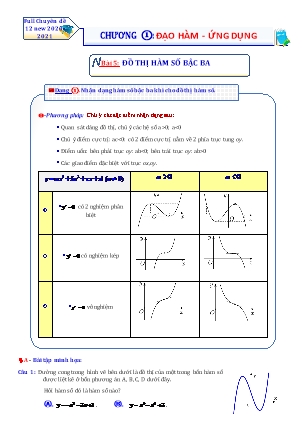
 Full Chuyên đề 
 12 new 2020-
 2021 CHƯƠNG ①: ĐẠO HÀM - ỨNG DỤNG 
 Bài 5: ĐỒ THỊ HÀM SỐ BẬC BA
  Dạng ①. Nhận dạng hàm số bậc ba khi cho đồ thị hàm số. 
 -Phương pháp: Chú ý các đặc điểm nhận dạng sau:
  Quan sát dáng đồ thị, chú ý các hệ số a >0; a<0
  Chú ý điểm cực trị: ac<0: có 2 điểm cực trị nằm về 2 phía trục tung oy.
  Điểm uốn: bên phải trục oy: ab0
  Các giao điểm đặc biệt với trục ox,oy.
 y ax3 bx2 cx d (a 0) a 0 a 0
  y' 0 có 2 nghiệm phân 
 
 biệt
   y' 0 có nghiệm kép
   y' 0 vô nghiệm
A - Bài tập minh họa: 
Câu 1: Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn hàm số 
 được liệt kê ở bốn phương án A, B, C, D dưới đây. 
 Hỏi hàm số đó là hàm số nào?
 Ⓐ. y x3 3x 1. Ⓑ. y x4 x2 3 .
 Ⓒ. y x3 3x 1. Ⓓ. y x2 3x 1.
 Lời giải PP nhanh trắc nghiệm
 Chọn C  Quan sát nhanh hệ số a
  Đồ thị hàm số đã cho là của hàm số bậc ba có hệ số a 0 nên  Nhìn dạng đồ thị
phương án đúng là hàm số y x3 3x 1.
Câu 2: Đường cong trong hình bên là đồ thị của hàm số nào dưới đây ? y
 3 3
 Ⓐ. y x 1. Ⓑ. y 4x 1. 2
 Ⓒ. y 3x2 1. Ⓓ. y 2x3 x2 .
 -1 O 1 x
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Nhìn dáng đồ thị bậc ba a<0
 Ta thấy đồ thị chứa A(1;0) , B(0;1) , C( 1;2) nên thay toạ độ các  Chú ý các giao điểm đặc biệt
điểm này vào đáp án có kết luận đồ thị là của hàm số y x3 1.
 Câu 3: Đường cong trong hình bên là đồ thị của một hàm số trong 
 bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi 
 hàm số đó là hàm số nào?
 Ⓐ. y x3 3x . Ⓑ. y x4 x2 1.
 Ⓒ. y x3 3x 1. Ⓓ. y x3 3x .
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Nhìn dáng đồ thị bậc ba a<0
 Dựa vào dáng điệu đồ thị suy ra hàm bậc ba có hệ số a 0 .  Chú ý đồ thị đi qua gốc tọa độ
Loại đáp án B và D.
Vì đồ thị đi qua gốc tọa độ nên loại đáp án C.
B - Bài tập rèn luyện:
Câu 1: Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm 
 số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là 
 hàm số nào?
 Ⓐ. y x3 3x 1. Ⓑ. y x3 3x 1.
 Ⓒ. y x3 3x 1. Ⓓ. y x3 3x2 1. Câu 2: Đường cong trong hình bên là hình dạng đồ thị của hàm số nào?
 Ⓐ. y x3 3x 1. Ⓑ. y x4 x2 1.
 Ⓒ. y x2 x 1. Ⓓ. y x3 3x 1.
Câu 3: Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn 
 hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi 
 hàm số đó là hàm số nào?
 Ⓐ. . y Ⓑ. x 3 . 3x 2 2 y x3 3x 2 2
 Ⓒ. . y Ⓓ.x3 3. x 2 2 y x3 3x 2 2
Câu 4: Đồ thị hình bên là đồ thị của hàm số nào trong các hàm số sau
 Ⓐ. y x3 3x2 1 Ⓑ. y x3 3x 1
 Ⓒ. y x3 3x 1 Ⓓ. y x3 3x2 1
Câu 5: Đường cong trong hình bên là hình dạng đồ thị của hàm số nào?
 Ⓐ. y x3 3x 1. Ⓑ. y x4 x2 1.
 Ⓒ. y x2 x 1. Ⓓ. y x3 3x 1.
Câu 6: Đường cong ở hình vẽ bên dưới là của đồ thị hàm số nào?
 Ⓐ. y x3 3x 4 . Ⓑ. y x3 3x2 2.
 Ⓒ. y x3 4 . Ⓓ. y x4 3x2 2 .
Câu 7: Đồ thị sau đây là của hàm số nào?
 Ⓐ. y x3 3x2 4. Ⓑ. y x3 3x2 4 .
 Ⓒ. y x3 3x2 4 . Ⓓ. y x3 3x2 4 .
Câu 8: Đường cong trong hình vẽ bên là đồ thị của hàm số nào
trong các hàm số được cho bởi các phương án
A, B, C, D dưới đây?
 Ⓐ. y 2x3 1. Ⓑ. y x3 x 1.
 Ⓒ. y x3 1. Ⓓ. y x3 2x 1. Câu 9: Đồ thị như hình vẽ là đồ thị của hàm số nào dưới đây?
 Ⓐ. y = x3 - 3x2 + 4. Ⓑ. y = - x3 +3x2 - 4
 Ⓒ. y = x3 - 3x2 - 4. Ⓓ. y = - x3 - 3x2 - 4.
 3 2
Câu 10: Cho hàm số y x 3x 2. Đồ thị của hàm số là hình nào dưới đây?
 Ⓐ. . Ⓑ. .
 Ⓒ. . Ⓓ. .
 BẢNG ĐÁP ÁN
 1.B 2.D 3.C 4.C 5.D 6.B 7.D 8.C 9.B 10.D
  Dạng ②. Biện luận số nghiệm của phương trình bằng đồ thị hàm số
 -Phương pháp: 
 Biện luận số nghiệm của phương trình f (x)= g(m)được 
 quy về tìm số giao điểm của đồ thị hàm số y = f (x)(C)
 và đường thẳng (d): y = g(m). 
 Có 2 cách biện luận số nghiệm của phương trình:
 . Biện luận số nghiệm của phương trình f (x)= g(m)bằng đồ thị ( khi bài toán cho 
 sẵn đồ thị): ta dựa vào sự tịnh tiến của đường thẳng (d): y = g(m)theo hướng 
 lên hoặc xuống trên trục tung.
 . Biện luận số nghiệm của phương trình f (x)= g(m)bằng bảng biến thiên ( bài 
 toán cho sẵn bảng biến thiên hoặc tự xây dựng)
A - Bài tập minh họa: 
 Câu 1: Cho hàm số y f x có bảng biến thiên như sau:
 Số nghiệm của phương trình f x 2 0 là
 Ⓐ. 1. Ⓑ. 2. Ⓒ. 3. Ⓓ. 0.
 Lời giải PP nhanh trắc nghiệm
 Chọn B  Vẽ đường thẳng y 2
 Ta có f x 2 0 f x 2.  Quan sát thấy 3 giao điểm
 Từ bảng biến thiên ta suy ra phương trình f x 2 có ba 
nghiệm phân biệt. 
Câu 2: Cho hàm số y ax3 bx2 cx d có đồ thị như hình bên dưới. Hỏi 
 phương trình ax3 bx2 cx d 2 0 có bao nhiêu nghiệm?
 Ⓐ. Phương trình có đúng một nghiệm.
 Ⓑ. Phương trình có đúng hai nghiệm.
 Ⓒ. Phương trình không có nghiệm.
 Ⓓ. Phương trình có đúng ba nghiệm.
 Lời giải PP nhanh trắc nghiệm
 Chọn B  Vẽ đường thẳng y 2
 3 2
 Ta có phương trình ax bx cx d 2 .  Quan sát thấy 3 giao điểm
Số nghiệm phương trình bằng số giao điểm của đường thẳng 
 y 2 và đồ thị hàm số y ax3 bx2 cx d . 
Từ đồ thị ta thấy có ba giao điểm. Vậy phương trình có ba 
nghiệm. Câu 3: Cho hàm số y f x liên tục trên đoạn 2; 4 và có đồ thị như hình 
 vẽ bên. Số nghiệm thực của phương trình 3 f x 4 0 trên đoạn 
 2; 4 là
 Ⓐ. 1. Ⓑ. 0.
 Ⓒ. 2.Ⓓ. 3.
 Lời giải PP nhanh trắc nghiệm
 Chọn D 4
  Vẽ đường thẳng y 
 4 3
  Ta có: 3 f x 4 0 f x 
 3  Quan sát thấy 3 giao điểm
 Số nghiệm của phương trình đã cho bằng số giao điểm của đồ 
 4
 thị hàm số y f x và đường thẳng y .
 3
 4
 Xét trên đoạn 2; 4 , đường thẳng y cắt đồ thị hàm 
 3
 y f x tại ba điểm. 
 Vậy phương trình 3 f x 4 0 có ba nghiệm trên đoạn 
 2; 4 
Câu 4: Tìm m để đồ thị hàm số y x3 3x2 m cắt trục hoành tại 3 điểm phân biệt?
 Ⓐ. m 4. Ⓑ. m  4;0. Ⓒ. m 4;0 . Ⓓ. m 0.
 Lời giải PP nhanh trắc nghiệm
 Chọn C  Cô lập m:
 Tập xác định: D ¡ . x3 3x2 m
 y 3x2 6x.  Casio tìm giá trị cực đại và cực 
 tiểu
Bảng biến thiên: m 0
 Yêu cầu bài toán thỏa khi 4 m 0.
 m 4 0
B - Bài tập rèn luyện:
Câu 1: Cho hàm số y f (x) xác định, liên tục trên ¡ và có bảng biến thiên như hình dưới đây. Đồ 
 thị hàm số y f (x) cắt đường thẳng y 2021 tại bao nhiêu điểm?
 Ⓐ. 2 . Ⓑ. 4 . Ⓒ. 1. Ⓓ. 0 .
Câu 2: Cho hàm số y f x liên tục trên đoạn  2;4 và có đồ thị như 
 hình bên. Số nghiệm thực của phương trình 3f x 5 0 trên 
 đoạn 0;4 là
 Ⓐ. 1. Ⓑ. 2.
 Ⓒ. 3. Ⓓ. 0.
Câu 3: Cho hàm số y f (x) có bảng biến thiên như sau:
 Số nghiệm của phương trình f (x) 2 0 là
 Ⓐ. 2. Ⓑ. 3. Ⓒ. 0. Ⓓ. 1.
Câu 4: Cho hàm số y f x có đồ thị như hình vẽ. Số nghiệm của phương trình 3f (x) 4 0 là
 y
 3
 Ⓐ. 1. Ⓑ. 3 .
 Ⓒ. 0 . Ⓓ. 2 . -1
 1 x
 -1
Câu 5: Cho hàm số f x ax3 bx2 cx d a,b,c,d ¡ có đồ thị như hình vẽ bên. Số nghiệm thực 
 của phương trình 4 f x 3 0 là Ⓐ. 3 . Ⓑ. 2 .
 Ⓒ. 1. Ⓓ. 0 . 
Câu 6: Cho hàm số y f (x) có bảng biến thiên như sau:
 Tập tất cả các giá trị của tham số m để phương trình f (x) m có ba nghiệm phân biệt là
 Ⓐ. (4; ) . Ⓑ. ( ; 2) . Ⓒ. [-2;4]. Ⓓ. ( 2;4) .
Câu 7: Cho hàm số f x có đồ thị như hình bên. Số nghiệm thực của phương 
 trình f 2 x 1 0 bằng
 Ⓐ. 3. Ⓑ. 6.
 Ⓒ. 4. Ⓓ. 1.
Câu 8: Cho hàm số f x ax3 bx2 cx d a 0 có đồ thị như hình 
 vẽ. Số nghiệm của phương trình 3f x 1 0 bằng
 Ⓐ. 0 . Ⓑ. 1.
 Ⓒ. 2 . Ⓓ. 3.
Câu 9: Đồ thị sau đây là của hàm số y = - x3 + 3x2 - 4 . Với giá trị nào 
 3 2
 của m thì phương trình x - 3x + m= 0 có hai nghiệm phân biệt. Hãy chọn câu trả lời đúng.
 ém = 0 ém = - 4
 Ⓐ. ê . Ⓑ. ê .
 ëêm = 4 ëêm = 4
 ém = - 4
 Ⓒ. ê . Ⓓ. m = 0 .
 ëêm = 0
Câu 10: Tìm số giá trị nguyên của m để phương trình x3 3x2 1 m 0 
 có 3 nghiệm phân biệt:
 Ⓐ. 4 . Ⓑ. 3 . Ⓒ. 2 . Ⓓ. 0 .
 BẢNG ĐÁP ÁN
 1.A 2.B 3.B 4.B 5.A 6.D 7.C 8.B 9.A 10.B  Dạng ③. Sự tương giao của 2 đồ thị (liên quan đến tọa độ giao điểm)
 -Phương pháp: Cho 2 hàm số y f x , y g x có đồ thị lần lượt là (C) và (C’)
 . Lập phương trình hoành độ giao điểm của và : f x g x , (1)
 . Giải phương trình (1) tìm x từ đó suy ra y và tọa độ giao điểm.
 . Số nghiệm của (1) bằng số giao điểm của hai đồ thị 
 y f x , y g x . 
 - Casio: Solve, table, giải phương trình cơ bản
A - Bài tập minh họa: 
 3
Câu 1: Có bao nhiêu giao điểm của đồ thị hàm số y x 3x 3 với trục Ox ?
 Ⓐ. 2 . Ⓑ. 3. Ⓒ. 0 .Ⓓ. 1
 Lời giải
 Lời giải PP nhanh trắc nghiệm
 Chọn D  Casio
  Ta có y 3x2 3 0;x ¡ , hàm số y f x luôn đồng 
biến trên ¡
 Bảng biến thiên 
 x + 
 y' +
 +
 y 
 Vậy đồ thị hàm số y x3 3x 3 và trục Ox có 1 giao điểm.
Câu 2: Biết rằng đường thẳng y 2x 2 cắt đồ thị hàm số y x3 x 2 tại điểm duy nhất có tọa độ 
 x0 ; y0 . Tìm y0 .
 Ⓐ. y0 0 . Ⓑ. y0 4 . Ⓒ. y0 2 . Ⓓ. y0 1.
 Lời giải PP nhanh trắc nghiệm
 Chọn C  Casio
 Ta có phương trình hoành độ giao điểm 
 x3 x 2 2x 2 x3 3x 0 x x2 3 0 x 0
Suy ra tọa độ giao điểm là 0; 2 . 3 2
Câu 3: Cho hàm số y 2x 3x 1. có đồ thị C và đường thẳng d : y x 1. Tìm số giao điểm của 
 C và d .
 Ⓐ. 3. Ⓑ. 2. Ⓒ. 0. Ⓓ. 1.
 Lời giải PP nhanh trắc nghiệm
 Chọn A  Casio
  Xét phương trình hoành độ giao điểm của C và d :
 2x3 3x2 1 x 1 2x3 3x2 1 x 1 0
 x1 1
 1 17
 2x3 3x2 x 2 0 x .
 2 4
 1 17
 x 
 3 4
 Phương trình có 3 nghiệm phân biệt nên C và d có 3 
giao điểm.
B - Bài tập rèn luyện:
Câu 1: Đồ thị của hàm số y x3 2 và đồ thị của hàm số y x 2 có tất cả bao nhiêu điểm chung.
 Ⓐ. 1. Ⓑ. 0 . Ⓒ. 3 . Ⓓ. 2 .
Câu 2: Cho hàm số y 2x3 3x2 1 có đồ thị C và đường thẳng d : y x 1. Số giao điểm của C 
 và d là
 Ⓐ. 1 . Ⓑ. 3. Ⓒ. 0 . Ⓓ. 2 .
 3
Câu 3: Đường thẳng có phương trình y 2x 1 cắt đồ thị của hàm số y x x 3 tại hai điểm A 
 và B với tọa độ được kí hiệu lần lượt là A xA; yA và B xB; yB trong đó xB xA . Tìm xB yB .
 Ⓐ. xB yB 5 Ⓑ. xB yB 2 Ⓒ. xB yB 4 Ⓓ. xB yB 7
Câu 4: Số giao điểm của đồ thị hàm số y (x 3)(x2 3x 2) với trục Ox là:
 Ⓐ. 0 . Ⓑ. 3. Ⓒ. 1. Ⓓ. 2 .
Câu 5: Biết rằng đường thẳng y 2x 3 và đồ thị hàm số y x3 x2 2x 3 có hai điểm chung phân 
 biệt A và B , biết điểm B có hoành độ âm. Tìm xB .
 Ⓐ. xB 1. Ⓑ. xB 5 . Ⓒ. xB 2 . Ⓓ. xB 0 .
Câu 6: Tìm tất cả các giá trị của tham số m để đồ thị hàm số y x3 3x2 cắt đường thẳng y m tại 
 ba điểm phân biệt.
 Ⓐ. m ; 4 . Ⓑ. m 0; .