Chuyên đề Giải tích Lớp 11 - Phương trình lượng giác có cách giải đặc biệt (Có lời giải)

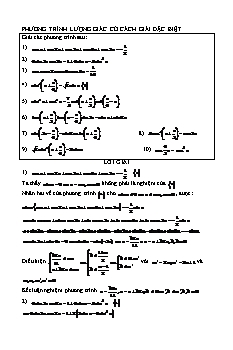
 PHƯƠNG TRÌNH LƯỢNG GIÁC CÓ CÁCH GIẢI ĐẶC BIỆT
Giải các phương trình sau:
 1
1). cos x cos 2x cos 3x cos 4x cos 5x 
 2
2). 4sin 3xcos 2x 1 6sin x 8sin3 x 
 1
3). cos xcos 2xcos 4xcos8x 
 16
 3 
4). sin x 2 sin x 1 
 4 
 4 4 7 
5). sin x cos x cot x cot x 
 8 3 6 
6). tan x tan x sin 3x sin x sin 2x 
 3 6 
 3 
7). sin 3x sin 2xsin x 8). 8cos x cos 3x 
 4 4 3 
 3 4 2
9). 2 sin x 2sin x 10). cos x cos x
 4 3
 LỜI GIẢI
 1
1). cos x cos 2x cos 3x cos 4x cos 5x 
 2
Ta thấy sin x 0 x m ,m ¢ không phải là nghiệm của 
Nhân hai vế của phương trình cho sin x 0 x m ,m ¢ , được:
 1
 sin x cos x cos 2x cos 3x cos 4x cos 5x sin x
 2
 1
 sin xcos x sin xcos 2x sin xcos 3x sin xcos 4x sin xcos 5x sin x
 2
 sin 2x sin x sin 3x sin 2x sin 4x sin 3x sin 5x sin 4x sin 6x sin x
 k2 
 sin 5x sin 6x 0 sin 6x sin( 5x) x  x h2 ,k,h ¢
 11
 11m
 k2 k 
 m 2 k 11m'
Điều kiện 11 với m' 2 m,n' 2 n 1 và 
 n 1 h n'
 h2 n h 
 2
 m,n,m',n' ¢ 
 k2 
Kết luận nghiệm phương trình x ,x h2 ; k 11m',h n',k,h ¢
 11
2). 4sin 3xcos 2x 1 6sin x 8sin3 x 
 4sin 3x.cos 2x 1 2 3sin x 4sin3 x 2sin x 2sin 5x 1 2sin 3x
Ta thấy cos x 0 x m ,m ¢ không phải là nghiệm của 
 2
Nhân hai vế của phương trình cho cos x 0 x m ,m ¢ , được:
 2
 2sin x 2sin 5x cos x 1 2sin 3x cos x
 sin 2 x sin 4 x sin 6 x cosx sin 2 x sin 4 x
 k2 h2 
 sin 6x cos x sin x x hoặc x ; k,h ¢
 2 14 7 10 5
 k2 3 7m
 m k 
 14 7 2 2
Điều kiện với m là số nguyên lẻ, và n là số 
 h2 2 5n
 n h 
 10 5 2 2
nguyên chẵn.
 1
3). cos xcos 2xcos 4xcos8x 
 16
Ta thấy sin x 0 x m ,m ¢ không phải là nghiệm của 
Nhân hai vế của phương trình cho sin x 0 x m ,m ¢ , được:
 16sinxcos xcos 2xcos 4xcos8x sin x
 8sin 2xcos 2xcos 4xcos8x sin x
 4sin 4xcos 4xcos8x sin x 2sin 8xcos8x sin x sin16x sin x
 k2 h2 
 x  x ; k,h ¢ 
 15 17 17
 k2 15m
 m k 
 15 2
Điều kiện với m là số nguyên chẵn và n là số 
 h2 17n 1
 n h 
 17 17 2
nguyên lẻ.
 3 
4). sin x 2 sin x 1 
 4 
Đặt t x x t 
 4 4
 3 3
 1 sin t 2 sin t sin t sin t cos t 
 4 
 sin3 t sin t cos t 0 sin t sin2 t 1 cos t 0
 cos2 t.sin t cos t 0 cos t 1 sin t.cos t 0 cos t 0  1 sin t.cos t 0 
Với: cos t 0 t k x k x k k ¢ 
 2 4 2 4
 1
Với 1 sin t.cos t 0 sin 2t 1 sin 2t 2 (vô nghiệm).
 2
Vậy nghiệm của phương trình: x k k ¢ 
 4
 4 4 7 
5). sin x cos x cot x cot x ( )
 8 3 6 
 sin x 0
 3 k 
ĐK: sin x sin x 0 cos 2x 0 x 
 3 6 6 3 2
 sin x 0
 6 
Có: cot x cot x cot x cot x cot x tan x 1.
 3 6 3 2 3 3 3 
 7 3 cos 4x 7 1 k 
 ( ) sin4 x cos4 x cos 4 x x : (thỏa đk).
 8 4 8 2 12 2
 k 
Kết luận: Tập nghiệm cần tìm của phương trình là x với k ¢ .
 12 2
6). tan x tan x sin 3x sin x sin 2x ( )
 3 6 
 k 
Điều kiện: cos x 0, cos x 0 x , với k ¢ . Ta có: 
 3 6 6 2
 tan x tan x tan x tan x cot x tan x 1. 
 3 6 2 6 6 6 6 
 ( ) sin 3x sin x sin 2x (sin 3x sin x) sin 2x 0
 2sin 2xcos x sin 2x 0 sin 2x(2cos x 1) 0 sin 2x 0  cos x 0,5
 k 2 
 x hoặc x k2 với k ¢ (thỏa mãn điều kiện).
 2 3
 k 2 
Kết luận: Các tập nghiệm cần tìm của phương trình là x , x k2 .
 2 3
7). sin 3x sin 2xsin x ( )
 4 4 
Nhận thấy: sin 3x sin 3x sin 3x sin 3 x 
 4 4 4 4 
Đặt t x , suy ra: x t nên phương trình đã cho:
 4 4
 3
 ( ) sin 3t sin 2t sin t 4sin t 3sin t cos 2t sin t 0
 2 4sin3 t 3sint (1 2sin2 t)sint 0 sint 0 hoặc sin2 t 1
 sin t 0 hoặc cos t 0 t k hoặc t k với k ¢ .
 2
 k 
Suy ra: x k hoặc x k x với k ¢ .
 4 4 4 2
 k 
Kết luận: Tập nghiệm cần tìm của phương trình là x , với k ¢ .
 4 2
 3 
8). 8cos x cos 3x ( )
 3 
Nhận thấy: cos 3x cos( 3x) cos 3 x  Đặt t x  
 3 3
 ( ) 8cos3 t cos3t 4cos3 t 3cost 12cos3 t 3cost 0
 1
 cos t 0 hoặc 4cos2 t 1 0 cos t 0 hoặc cos 2t 
 2
 t k hoặc t k . Suy ra: x k hoặc x k với k ¢ .
 2 3 2
Kết luận: Các tập nghiệm cần tìm của phương trình là x k , x k .
 2
 3 
9). 2 sin x 2sin x ( ) . Đặt t x x t 
 4 4 4
 3 3 2 2
 ( ) sin t 2 sin t sin t sin t cos t (sin t cos t)(sin t cos t)
 4 
 cost( sin2 t sintcost cos2 t) 0 cost(sin2t 2) cost 0  sin2t 2
 t k . Suy ra: x k với k ¢ .
 2 4
Kết luận: Tập nghiệm cần tìm của phương trình là x k với k ¢ .
 4
PHƯƠNG TRÌNH LƯỢNG GIÁC ĐẶC BIỆT
Giải các phương trình sau: 
1). 3tan2 x 4sin2 x 2 3 tan x 4sin x 2 0
2). sin 4x cos 4x 1 4 2 sin x 
 4 
3). sin 3x cos x 2sin 3x cos 3x 1 sin x 2cos 3x 0
4). cos 2x 3 sin 2x 3 sin x cos x 4 0 . 
5). cos 2x cos2 x 1 tan x . 
6). cos 3x 2 cos2 3x 2(1 sin2 2x)
7). sin1996 x cos1996 x 1
8). sin4 x cos15 x 1 2 2 
9). 2cos cos x 1 cos sin 2x 
 2 
 LỜI GIẢI
1). 3tan2 x 4sin2 x 2 3 tan x 4sin x 2 0
 3tan2 x 2 3 tan x 1 4sin2 x 4sin x 1 0
 2 2
 3 tan x 1 2sin x 1 0
 x k 
 3 6
 tan x 
 3 tan x 1 0 3 
 x k2 
 2sin x 1 0 1 6
 sin x 
 2 5 
 x k2 
 6
Biểu diễn nghiệm trên vòng tròn lượng giác:
 sin
 5π π
 6 6
 cos
 0
 7π
 6
 7 
Nghiệm của 3 tan x 1 0 được biểu diễn hai đầu mút là , .
 6 6
 5 
 Nghiệm của 2sin x 1 0 được biểu diễn hai đầu mút là , .
 6 6
Kết luận nghiệm của phương trình: x k2 
 6
2). sin 4x cos 4x 1 4 2 sin x sin 4x 1 cos 4x 4 sin x cos x 
 4 
 2sin 2xcos 2x 2cos2 2x 4 sin x cos x 
 cos x sin x cos x sin x sin 2x cos 2 x 2 sin x cos x 
 cos x sin x cos x sin x sin 2x cos 2 x 2 0
 cos x sin x 0 hoặc cos x sin x sin 2x cos 2 x 2 0 (2)
Giải (1) 2 cos x 0 x k ,k ¢
 4 4 
Giải 2 2cos x cos 2x 2 0 cos x sin 3x 2 
 4 4 
 x k2 
 cos x 1 
 m2 ; m,k ¢ . Hệ (1) có nghiệm khi và chỉ khi
 sin 3x 1 x 
 6 3
 m2 
k2 12k 4m 1 phương trình này vô nghiệm vì vế trái luôn là 
 6 3
một số nguyên chẵn, còn vế phải là số nguyên lẻ. Kết luận (2) vô nghiệm.
Nghiệm phương trình x k ,k ¢
 4
3). sin 3x cos x 2sin 3x cos 3x 1 sin x 2cos 3x 0
 sin 3xcos x cos 3xsin x 2 sin2 3x cos2 3x cos 3x 0
 sin 4x 2 cos 3x 0
 k 
 x 
 sin 4x 1 4x k2 8 2
 sin 4x cos 3x 2 2 , k,m ¢ 
 cos 3x 1 m2 
 3x m2 x 
 3
Nếu phương trình có nghiệm thì tồn tại các giá trị k, m sao cho : 
 k m2 k 2m 1 3k 4m 1
 12k 16m 3 
8 2 3 2 3 8 6 8
 2 6k 8m 3 (không thỏa). Phương trình vô nghiệm vì: Vế trái là một số 
chẵn, còn vế phải là một số lẻ .
Kết luận phương trình vô nghiệm.
4). cos 2x 3 sin 2x 3 sin x cos x 4 0 . Chia 2 vế cho 2 ta được :
 1 3 3 1 
 cos 2x sin 2x sin x cos x 2 0 sin 2x sin x 2
 2 2 2 2 3 6 
 sin 2x 1 2x k2 x k 
 3 3 2 12
 . Phương trình có 
 sin x 1 x l2 x l2 
 6 6 2 3
nghiệm khi : k l2 1 12k 4 24l 12k 24l 5 . Vô nghiệm 
 12 3
với mọi k, l ¢ vì VT là một số chẵn, còn VP là một số lẻ .
 cosx 0
5). cos 2x cos2 x 1 tan x . Điều kiện : * .
 tanx -1
Đặt t tan x , điều kiện t 0
 Khi đó phương trình trở thành : 1 t2 1
 1 t 1 t2 1 t , điều kiện 1 t2 0 0 t 1 .
 1 t2 1 t2
 2 2
 1 t2 1 t 1 t 1 t 1 t 1 0 .
 2 1 5 1 5
 1 t 1 t 1 0 t3 t2 t 0 t 0  t  t .
 2 2
So với điều kiện nhận t 0 tan x 0 x k , k ¢ 
6). cos 3x 2 cos2 3x 2(1 sin2 2x) Ta có nhận xét sau :
Bất đẳng thức Bunhiacopxki: 
 2
 2 2 2 2 2 
 cos 3x 2 cos 3x 1 1 cos 3x 2 cos 3x 
 cos 3x 2 cos2 3x 2
Suy ra vế trái đạt giá trị lớn nhất bằng 2 khi cos 3x 2 cos2 3x
 VP 2(1 sin2 2x) 2
Vậy chỉ xảy ra khi : 
 k 
 2 2 x 
 cos 3x 2 cos 3x cos 3x 1 cos6x 1 6 3
 .
 2 sin 2x 0 sin 2x 0 l 
 sin 2x 0 x 
 2
Nếu phương trình có nghiệm thì tồn tại k,l thuộc Z sao cho :
 k l 3l 1 l 1
 1 2k 3l k l . 
 6 3 2 2 2
Để k là nguyên thì ta chọn : l 1 2n l 2n 1 .
 2n 1 
Thay vào (2) nghiêm : x n n Z 
 2 2
7). sin1996 x cos1996 x 1
 sin1996 x cos1996 x sin2 x cos2 x sin1996 x sin2 x cos2 x cos1996 x
 sin2 x sin1994 1 cos2 x 1 cos1994 x 2 
 sin2 x 0
Ta thấy sin2 x sin1994 1 0,x 
 1994 
 sin 1 1
 cos2 x 0
Ngoài ra có cos2 x 1 cos1994 x 0,x .
 1994 
 1 cos x 0 x m 
 sin x 0 
 2 1994 x m 
 sin x sin 1 0 sin x 1 2
Do đó 2 , m,n ¢ 
 cos2 x 1 cos1994 x 0 cos x 0 
 x n 
 cos x 1 2
 x n 
 k 
Vậy nghiệm của phương trình là: x , k ¢ .
 2
8). sin4 x cos15 x 1
 sin4 x cos15 x sin2 x cos2 x sin4 x sin2 x cos2 x cos15 x
 sin2 x sin2 x 1 cos2 x 1 cos13 x 1 
 sin2 x 0
Vì sin2 x sin2 x 1 0,x , 
 2 
 sin x 1 0
 cos2 x 0
và cos2 x 1 cos13 x 0,x
 13 
 1 cos x 0
 2 2
 sin x sin x 1 0
Từ đó 1 
 2 13 
 cos x 1 cos x 0
 x m 
 sin2 x 0 sin x 0 
 2 x m 
 sin x 1 sin x 1 2
 , m,n ¢ .
 cos2 x 0 cos x 0 
 x n 
 13 cos x 1 2
 cos x 1 
 x n2 
Vậy nghiệm của phương trình là: x k ,x k2 , k ¢ .
 2
 2 2 
9). 2cos cos x 1 cos sin 2x 
 2 
 2 2 
 2cos cos x 1 cos sin 2x 
 2 
 cos2 x sin 2x k2 
 cos cos2 x cos sin 2x 
 2
 cos x sin 2x k2 
 cos2 x sin 2x k2
 2
 cos x sin 2x k2 1 cos 2x
 sin 2x k2
 2 cos 2x 2sin 2x 4k 1 (1)
 1 cos 2x cos 2x 2sin 2x 4k 1 (2)
 sin 2x k2 
 2
Điều kiện để phương trình (1) hoặc phương trình (2) có nghiệm là:
 2 1 5 1 5
 12 22 4k 1 16k2 8k 4 0 k , vì k ¢ nên chọn 
 4 4
 k 0
Thay k 0 vào (1) được 
 cos 2x 2sin 2x 1 1 cos 2x 2sin 2x 0 2cos2 x 4sin xcos x 0
 cos x 0 x k 
 cos x 0 2
 2cos x cos x 2sin x 0 1 
 cos x 2sin x tan x 1 
 2 x arctan k 
 2 
Thay k 0 vào (1) được 
 cos 2x 2sin 2x 1 1 cos 2x 2sin 2x 0 2cos2 x 4sin xcos x 0
 cos x 0 x k 
 cos x 0 2
 2cos x cos x 2sin x 0 1 
 cos x 2sin x tan x 1 
 2 x arctan k 
 2