Chuyên đề Giải tích Lớp 11 - Phương trình lượng giác cơ bản (Có lời giải)

 PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
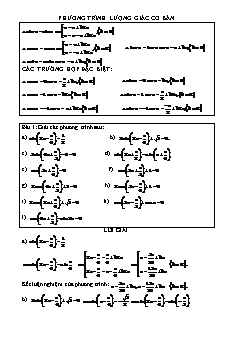
 u v k2 
 sin u sin v , k Z 
 u v k2 
 u v k2 
 cos u cos v , k Z tan u tan v u v k , k Z 
 u v k2 
 cot u cot v u v k , k Z 
CÁC TRƯỜNG HỢP ĐẶC BIỆT:
 cos u 0 u k , k Z sin u 0 u k , k Z 
 2
 cos u 1 u k2 k Z sin u 1 u k2 , k Z 
 2
 cos u 1 u k2 k Z sin u 1 u k2 , k Z 
 2
Bài 1: Giải các phương trình sau: 
 1 
a). sin 2x b). 2sin 2x 3 0.
 4 2 4 
c). 3sin 4x 4 0 d). sin 2x sin x 
 3 2 4 
e). cos 3x 0 f). cos 5x 1 0
 4 3 
g). 2cos 4x 5 0 h). 2cos 3x 1 0
 5 4 
i). 2cos 2x 3 0 k). cos 3x cos x 0
 6 3 
l). cos 4x sin 2x 0
 5 
 LỜI GIẢI
 1
a). sin 2x 
 4 2
 5 
 2x k2 x k 
 4 6 24
 sin 2x sin k Z . 
 4 6 13 
 2x k2 x k 
 4 6 24
 5 13 
Kết luận nghiệm của phương trình: x k ,x k k Z . 
 24 24
 3 
b). 2sin 2x 3 0 sin x sin 2x sin 
 4 4 2 4 3 
 2x k2 2x k2 x k 
 4 3 4 3 24 k Z . 
 19 
 2x k2 2x k2 x k 
 4 3 4 3 24
 19 
Kết luận nghiệm của phương trình: x k2 ,x k k Z . 
 24 24
 4
c). 3sin 4x 4 0 sin 4x 
 3 3 3
Vì 1 sin 4x 1 phương trình vô nghiệm.
 3 
d). sin 2x sin x 
 2 4 
 2x x k2 x k2 
 2 4 
 4 k Z .
 k2 
 2x x k2 x 
 2 4 12 3
 k2 
Kết luận nghiệm của phương trình: x k2 ,x k Z . 
 4 12 3
 k 
e). cos 3x 0 3x k x k Z . 
 4 4 2 12 3
 k 
Kết luận nghiệm của phương trình: x k Z . 
 12 3
f). cos 5x 1 0
 3 
 2 k2 
 cos 5x 1 5x k2 x k Z . 
 3 3 15 5
 2 k2 
Kết luận nghiệm của phương trình: x k Z . 
 15 5
g). 2cos 4x 5 0 
 5 
 5 
 cos 4x . Vì 1 cos 4x 1 phương trình vô nghiệm.
 5 2 5 
 1 2 
h). 2cos 3x 1 0 cos 3x cos 3x cos 
 4 4 2 4 3
 2 11 k2 
 3x k2 x 
 4 3 36 3 k Z . 
 2 5 k2 
 3x k2 x 
 4 3 36 3
 11 k2 5 k2 
Kết luận nghiệm của phương trình: x ,x k Z . 
 36 3 36 3 3 5 
i). 2cos 2x 3 0 cos 2x cos 2x cos 
 6 6 2 6 6
 5 
 2x k2 x k 
 6 6 3 
 5 
 2x k2 x k 
 6 6 2
Kết luận nghiệm của phương trình: x k ,x k k Z . 
 3 2
k). cos 3x cos x 0 cos 3x cos x cos 3x cos x 
 3 3 3 
 2 
 3x x k2 x k 
 3 3 k Z . 
 k 
 3x x k2 x 
 3 6 2
 2 
Kết luận nghiệm của phương trình: x k ,x k k Z . 
 3 6
l). cos 4x sin 2x 0 cos 4x sin 2x cos 4x cos 2x 
 5 5 5 2 
 k 
 4x 2x k2 x 
 5 2 20 3 k Z . 
 7 
 4x 2x k2 x k 
 5 2 20
 k 7 
Kết luận nghiệm của phương trình: x ,x k k Z .
 20 3 20
Bài 2: Giải các phương trình sau:
 2 9 2 7 
a) sin 3x cos x b) sin 3x sin x 0 
 3 4 3 5 
 2 1
c) sin 2x cos x 0 d) sin 2x 
 4 4 2
 2 2 2 7 2 2 
 e) sin 3x sin x f). sin 5x cos 3x 0 
 3 5 3 4 
 4 4 
 g). sin 3x sin 3x 3 h). sin x cos x 3
 5 5 9 18 
 LỜI GIẢI
 2 9 
a). sin 3x cos x 
 3 4 
 2 2 
 sin 3x cos x 2 sin 3x cos x 
 3 4 3 4 
 2 2 3 
 sin 3x sin x sin 3x sin x 
 3 2 4 3 4 2 3 k 
 3x x k2 x 
 3 4 
 48 2 k Z . 
 2 3 5 
 3x x k2 x k 
 3 4 24
 k 5 
Kết luận: x ,x k k Z . 
 48 2 24
 2 7 2 2 
b). sin 3x sin x 0 sin 3x sin x 0 
 3 5 3 5 
 2 2 2 2 
 sin 3x sin x 0 sin 3x sin x 
 3 5 3 5 
 2 2 8 
 3x x k2 x k 
 3 5 
 15 k Z . 
 2 2 11 k 
 3x x k2 x 
 3 5 60 2
 8 11 k 
Kết luận nghiệm của phương trình: x k ,x , k Z . 
 15 60 2
c). sin 2x cos x 0 sin 2x sin x 0 
 4 4 2 
 sin 2x sin x sin 2x sin x 
 4 2 4 2 
 3 
 2x x k2 x k2 
 4 2 
 4 k Z . 
 5 k2 
 2x x k2 x 
 4 2 12 3
 3 5 k2 
Kết luận nghiệm của phương trình: x k2 ,x k Z . 
 4 12 3
 1 cos 2 2x 
 2 1 4 1 
d). sin 2x cos 4x 0 
 4 2 2 2 2 
 k 
 4x k x k Z . 
 2 2 4 4
 k 
Kết luận nghiệm của phương trình: x .
 4 4
 4 14 
 1 cos 6x 1 cos 2x 
 2 2 2 7 3 5 
e). sin 3x sin x 
 3 5 2 2
 4 14 4 14 
 1 cos 6x 1 cos 2x cos 6x cos 2x 
 3 5 3 5 
 4 4 4 4 
 cos 6x cos 2 2x cos 6x cos 2x 
 3 5 3 5 4 4 k 
 6x 2x k2 x 
 3 5 15 4 k Z . 
 4 4 8 k 
 6x 2x k2 x 
 3 5 15 2
 k 8 k 
Kết luận nghiệm của phương trình: x ,x , k Z 
 15 4 15 2
 2 2 
f) sin 5x cos 3x 0 
 3 4 
 2 
 1 cos 10x 1 cos 6x 
 3 2 2 
 0 cos 10x cos 6x 0 
 2 2 3 2 
 2 2 
 cos 10x cos 6x cos 10x cos 6x 
 3 2 3 2 
 2 3 5 k 
 10x 6x k2 x 
 3 2 24 2 k Z . 
 2 3 13 k 
 10x 6x k2 x 
 3 2 96 8
 5 k 13 k 
Kết luận nghiệm của phương trình: x ,x + k Z . 
 24 2 96 8
 4 
g). sin 3x sin 3x 3 
 5 5 
 4 4 
Các bạn để ý: 3x 3x . Từ đó suy ra: sin 3x sin 3x 
 5 5 5 5 
 3 
 2sin 3x 3 sin 3x sin 3x sin 
 5 5 2 5 3
 2 k2 
 3x k2 x 
 5 3 45 3 , k Z . 
 7 k2 
 3x k2 x 
 5 3 45 3
 2 k2 7 k2 
Kết luận nghiệm của phương trình: x ,x k Z . 
 45 3 45 3
 4 
h). sin x cos x 3 
 9 18 
 4 4 
Các bạn để ý: x x cos x sin x 
 9 18 2 18 9 
 4 4 3 4 
 2sin x 3 sin x sin x sin 
 9 9 2 9 3
 4 
 x k2 x k2 
 9 3 9 k Z . 
 4 2 
 x k2 x k2 
 9 3 9 2 
Kết luận nghiệm của phương trình: x k2 ,x k2 k Z . 
 9 9
Bài 3: Giải các phương trình sau:
 2 2
a) cos 4x sin x 0 b) cos 3x cos x c)
 3 4 3 
 2 3 2 2 
 cos 2x d). cos 2x sin x e)
 4 4 4 3 
 5 
 cos 3x sin 3x 2 
 3 6 
 LỜI GIẢI
a). cos 4x sin x 0 
 3 4 
 cos 4x sin x cos 4x sin x 
 3 4 3 4 
 cos 4x cos x cos 4x cos x 
 3 2 4 3 4 
 k2 
 4x x k2 x 
 3 4 36 3 k Z . 
 7 k2 
 4x x k2 x 
 3 4 60 5
 k2 7 k2 
Kết luận nghiệm của phương trình: x ,x k Z . 
 36 3 60 3
 2 2
b). cos 3x cos x 
 3 
 2 
 1 cos 6x 
 3 1 cos 2x 2 
 1 cos 6x 1 cos 2x 
 2 2 3 
 2 k 
 6x 2x k2 x 
 2 3 6 2
 cos 6x cos 2x k Z . 
 3 2 k 
 6x 2x k2 x 
 3 12 4
 k k 
Vậy nghiệm của phương trình: x ,x k Z . 
 6 2 12 4
 1 cos 4x 
 2 3 2 3 3
c). cos 2x 1 cos 4x 
 4 4 2 4 2 2
 1 
 sin 4x sin 4x sin (vì sin cos( ) )
 2 6 2 k 
 4x k2 x 
 6 24 2 k Z . 
 5 k 
 4x k2 x 
 6 24 2
 5 k k 
Kết luận nghiệm của phương trình: x ,x k Z . 
 24 2 24 2
 2 2 
d). cos 2x sin x 
 4 3 
 2 
 1 cos 4x 1 cos 2x 
 2 3 2 
 1 cos 4x 1 cos 2x 
 2 2 2 3 
 2 2 
 cos 4x cos 2x cos 4x cos 2x 
 2 3 2 3 
 5 7 
 4x 2x k2 x k 
 2 3 12 k Z . 
 5 13 k 
 4x 2x k2 x 
 2 3 36 3
 7 13 k 
Kết luận nghiệm của phương trình: x k ,x k Z . 
 12 36 3
 5 
e). cos 3x sin 3x 2 
 3 6 
 5 5 
Ta có: 3x 3x sin 3x cos 3x 
 6 3 2 6 3 
 2cos 3x 2 cos 3x 1 3x k2 
 3 3 3
 k2 
 x , k Z . 
 9 3
 k2 
Kết luận nghiệm của phương trình: x k Z . 
 9 3
Bài 4: Giải các phương trình sau:
a). 3tan 2x 3 b) 3cot 2x 3 c). 
 6 4 
 tan 3x 1 0 d). cot 3x 1 0 e).
 4 6 
 tan 3x tan 2x 0 
 4 
f). tan 4x tan 2x 0 g). tan 3x cot x 
 3 6 5 
 LỜI GIẢI 3
a). 3tan 2x 3 tan 2x 
 6 6 3
 k 
 tan 2x tan 2x k x k Z . 
 6 6 6 6 2
 k 
Kết luận nghiệm của phương trình: x k Z . 
 2
 3 
b). 3cot 2x 3 cot 2x cot 2x cot 
 4 4 3 3 3 
 k 
 2x k x k Z . 
 3 3 3 2
 k 
Kết luận nghiệm của phương trình: x k Z . 
 3 2
c). tan 3x 1 0 tan 3x 1 
 4 4 
 k 
 tan 3x tan 3x k x k Z . 
 4 4 4 4 6 3
 k 
Kết luận nghiệm của phương trình: x k Z . 
 6 3
d). cot 3x 1 0 cot 3x 1 
 6 6 
 k 
 cot 3x cot 3x k x k Z . 
 6 4 6 4 36 3
 k 
Kết luận nghiệm của phương trình: x k Z . 
 36 3
e). tan 3x tan 2x 0 tan 3x tan 2x tan 3x tan 2x 
 4 4 4 
 k 
 3x 2x k x k Z . 
 4 20 5
 k 
Kết luận nghiệm của phương trình: x k Z . 
 20 5
f). tan 4x tan 2x 0 
 3 6 
 k 
 tan 4x tan 2x 4x 2x k x k Z . 
 3 6 3 6 36 6
 k 
Kết luận nghiệm của phương trình: x k Z . 
 36 6
g). tan 3x cot x 
 5 
 7 k 
 tan 3x tan x 3x x k x k Z . 
 5 2 5 2 40 4 7 k 
Vậy nghiệm của phương trình: x k Z . 
 40 4
Bài 5: Giải các phương trình sau:
 1 1
a). sin x 600 b). cos 2x 500 
 2 2
 0 3 x 0 3
c). tan 3x 30 d). cot 20 
 3 2 3
 LỜI GIẢI
 1
a). sin x 600 
 2
 x 600 300 k3600 x 900 k3600
 sin x 600 sin 300 
 0 0 0 0 0 0
 x 60 180 30 k360 x 210 k360
Kết luận nghiệm của phương trình x 900 k3600 , x 2100 k3600 k ¢ 
 1
b). cos 2x 500 
 2
 2x 500 600 k3600 x 50 k1800
 cos 2x 500 cos600 
 0 0 0 0 0
 2x 50 60 k360 x 55 k180
Kết luận nghiệm của phương trình x 50 k1800 ,x 550 k1800 , (k ¢ )
 3
c). tan 3x 300 
 3
 tan 3x 300 tan( 300 ) 3x 300 300 k1800 x k600
Kết luận nghiệm của phương trình x k600 , k ¢ .
 x 0 3
d). cot 20 
 2 3
 x 0 0 x 0 0 0 0 0
 cot 20 cot 60 20 60 k180 x 160 k360
 2 2
Kết luận nghiệm của phương trình x 1600 k3600 , k ¢ .
Bài 6: Giải các phương trình sau:
 x x 
a). 1 2cos x 3 cos x 0 b). cot 1 cot 1 0
 3 2 
c). tan x 300 cos 2x 1500 0 d). 3tan x 3 2sin x 1 0
 0 0
e). cos 2xcot x 0 f). tan 2x 60 cos x 75 0
 4 
h). cot x 1 sin 3x 0 k). tan x tan 2x 1
 LỜI GIẢI 1
 1 2cos x 0 cos x 
a). 1 2cos x 3 cos x 0 2 
 3 cos x 0 
 cos x 3
 1 2 2 
Với cos x cos x cos x k2 , k ¢ 
 2 3 3
Với cos x 3 phương trình vô nghiệm.
 2 
 Kết luận nghiệm của phương trình x k2 , k ¢ 
 3
 x x 
b). cot 1 cot 1 0 (1)
 3 2 
 x x
 sin 0 k 
 3 3 x k3 
Điều kiện: , k ¢ 
 x x x k2 
 sin 0 k 
 2 2
 x x x 3 
 cot 1 0 cot 1 k x k3 
 1 3 3 3 4 4 , k ¢ 
 x x x 
 cot 1 0 cot 1 k x k2 
 2 2 2 4 2
So với điều kiện các nghiệm này thỏa.
 3 
Vậy phương trình có nghiệm: x k3 ,x k2 , k ¢ .
 4 2
c). tan x 300 cos 2x 1500 0 (1)
Điều kiện: cos x 300 0 x 300 900 k1800 x 1200 k1800 , k ¢ .
 x 300 k1800 x 300 k1800
 tan x 300 0 
 1 2x 1500 900 k3600 x 1200 k1800 , k ¢ 
 0 
 cos 2x 150 0 0 0 0 0 0
 2x 150 90 k360 x 30 k180
So với điều kiện nghiệm x 1200 k1800 loại.
Vậy phương trình có nghiệm: x 300 k1800 , k ¢ 
d). 3tan x 3 2sin x 1 0 (1). Điều kiện cos x 0 x k , k ¢ .
 2
 5 
 x k 
 3 6
 tan x 
 3tan x 3 0 
 1 3 x k2 , k ¢ 
 2sin x 1 0 1 6
 sin x 5 
 2 x k2 
 6
 5 
So với điều kiện các nghiệm này thỏa. Vì tập các giá trị x k2 ,k ¢  
 6 
 5 
là tập con của tập các giá trị x k ,k ¢  .
 6 