Chuyên đề Giải tích Lớp 11 - Phần 2: Phương trình lượng giác tổng hợp (Có lời giải)

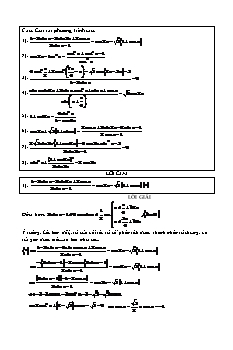
 Câu : Giải các phương trình sau:
 1 2sin x 2sin 2x 2cos x
1). cos 2x 3 1 cos x 
 2sin x 1
 cos2 x cos3 x 1
2). cos 2x tan2 x 
 cos2 x
 2 x 2 7 
 4cos 2cos x 3 cos 2x 3 3
 2 4 
3). 0 
 1 2sin x
 sin x.sin 2x 2sin x.cos2 x sin x cos x
4). 6 cos 2x 
 sin x 
 4 
 4sin2 x
5). 1 cot 2x 
 1 cos 4x
 2cos x 2sin 2x 2sin x 1
6). cos 2x 3 1 sin x 
 2cos x 1
 2 3 sin 2x 1 cos 2x 4cos 2x.sin2 x 3
7). 0 
 2sin 2x 1
 (1 cos 2x)2
8). sin2 x 2cos 2x 
 2sin 2x
 LỜI GIẢI
 1 2sin x 2sin 2x 2cos x
1). cos 2x 3 1 cos x 
 2sin x 1
 LỜI GIẢI
 x k2 
 1 6
Điều kiện: 2sin x 1 0 sin x , k ¢ 
 2 5 
 x k2 
 6
Ý tưởng: Các bạn để ý: tử của vế trái, tử số phân tích được thành nhân tử chung, và 
rút gọn được mẫu...ta làm như sau:
 1 2sin x 4sin xcos x 2cos x
 cos 2x 3 1 cos x 
 2sin x 1
 2sin x 1 2cos x 2sin x 1 
 cos 2x 3 1 cos x 
 2sin x 1
 2sin x 1 1 2cos x 
 cos 2x 3 1 cos x 
 2sin x 1
 1 2cos x 2cos2 x 1 3 3 cos x 
 3
 2cos2 x 2 3 cos x 3 0 cos x  cos x 1 
 2 3 
Với cos x cos x cos x k2 , k Z 
 2 6 6
Với cos x 1 x k2 k Z . 
Kết hợp với điều kiện nghiệm của phương trình: 
 x k2 ; x k2 , k Z . 
 6
 cos2 x cos3 x 1
2). cos 2x tan2 x 
 cos2 x
 LỜI GIẢI
Điều kiện: cos x 0. 
Ý tưởng: Biến đổi VP ta rút gọn được tan2 x ....
 cos2 x cos2 x 1 1
 cos 2x tan2 x cos 2x tan2 x 1 cos x 
 cos2 x cos2 x cos2 x cos2 x
 cos 2x tan2 x 1 cos x 1 tan2 x 
 1
 2cos2 x 1 cos x 0 2cos2 x cos x 1 0 cos x 1 hoặc cos x .
 2
So với điều kiện cos x 0 hai giá trị này đều nhận.
Với cos x 1 x k2 k Z . 
 1 2 2 
Với cos x cos x cos x k2 k Z . 
 2 3 3
 2 2 
Nghiệm của phương trình: x k2 ; x k2 ; x k2 , k Z . 
 3 3
 2 x 2 7 
 4cos 2cos x 3 cos 2x 3 3
 2 4 
3). 0 
 1 2sin x
 LỜI GIẢI
 x k2 
 1 6
Điều kiện: 1 2sin x 0 sin x sin x sin , k Z . 
 2 6 5 
 x k2 
 6
Ý tưởng: Hạ bậc, sau đó rút gọn...
 x 1 cos x
Ta có: g 4cos2 4. 2 1 cos x . 
 2 2
 2 7 7 
 g 2cos x 1 cos 2x 1 cos 3 2x 
 4 2 2 
 1 cos 2x 1 sin 2x. 
 2 
 2 1 cos x 1 sin 2x 3 cos 2x 3 0 3 cos 2x sin 2x 2cos x 0 3 cos 2x sin 2x 2cos x 
 3 1 
 cos 2x sin 2x cos x cos 2x.cos sin 2x.sin cos x 
 2 2 6 6
 5 k2 7 
 cos 2x cos x x hoặc x k2 , k Z 
 6 18 3 6
Biểu diễn nghiệm
 5π
 7π π
 - 5π 18
 6 6
 17π 6
 18
 29π
 18
 7 5 7 
Ta thấy hai đầu mút và trùng nhau, vậy nghiệm x k2 loại.
 6 6 6
 5 k2 5 17 29 
Còn nghiệm x được biểu diễn ba đầu mút , , đều khác 
 18 3 18 18 18
 5 5 k2 
hai đầu mút và . Vậy nghiệm x nhận.
 6 6 18 3
 5 k2 
Kết luận nghiệm phương trình x .
 18 3
 k2 
Để biết nghiệm x , k,n ¢ , có bao nhiêu đầu mút, ta lấy 
 n
 k2 
 k2 : n vậy nghiệm này có n đầu mút, sau đó chọn k = 0,1, 2, 3,..., n – 1.
 n 
 sin x.sin 2x 2sin x.cos2 x sin x cos x
4). 6 cos 2x 
 sin x 
 4 
 LỜI GIẢI
Điều kiện: sin x 0 x k x k ,k ¢ 
 4 4 4
 2sin2 x.cos x 2sin x.cos2 x sin x cos x
 6 cos 2x 
 sin x 
 4 
 2sin x.cos x sin x cos x sin x cos x 
 6 cos 2x 
 sin x 
 4 sin x cos x 1 2sin xcos x 3 cos 2x sin x cos x 
 1 2sin xcos x 3 cos2 x sin2 x 
 2
 sin x cos x 3 sin x cos x sin x cos x 
 sin x cos x 3 sin x cos x 
 1 3 sin x 3 1 cos x 
 3 1 5 5 
 tan x tan x tan x k , k Z .
 1 3 12 12
 5 
So với điều kiện nghiệm của phương trình x k , k Z 
 12
 4sin2 x
5). 1 cot 2x 
 1 cos 4x
 LỜI GIẢI
 sin 2x 0 sin 2x 0
Điều kiện: 
 1 cos 4x 0 cos 4x 1
 cos 2x 4sin2 x
 1 
 sin 2x 2sin2 2x
 sin 2x cos 2x 2sin2 x
 sin 2x sin2 2x
 sin 2x cos 2x sin 2x 1 cos 2x 
 sin2 2x 1 sin 2xcos 2x cos 2x 0 
 sin 2x 1 sin 2x 1 cos 2x sin 2x 1 0 
 sin 2x 1 sin 2x 1 cos 2x 0 
 sin 2x 1 0  sin 2x cos 2x 1 0 
Với sin 2x 1 0 sin 2x 1 (nhận) 2x k2 x k . 
 2 4
Với sin 2x cos 2x 1 cos 2x cos x k hoặc x k .
 4 4 4
Ta thấy x k thì sin 2x sin k2 1 0 và 
 4 2 
 cos 4x cos k4 1 0 . Vậy nghiệm x k nhận.
 4
Tương tự thay 2 nghiệm x k , x k thì nghiệm x k làm sin 2x = 0, 
 4
nên nghiệm này bị loại.
So với điều kiện nghiệm của phương trình: x k ; x k k Z 
 4 4 2cos x 2sin 2x 2sin x 1
6). cos 2x 3 1 sin x 
 2cos x 1
 LỜI GIẢI
 1 
Điều kiện: 2cos x 1 0 cos x x k2 , k Z . 
 2 3
Phân tích tử số của VP thành nhân tử, sau đó rút gọn...
 2cos x 1 2sin x 2cos x 1 
 cos 2x 3 1 sin x 
 2cos x 1
 2cos x 1 1 2sin x 
 cos 2x 3 1 sin x 
 2cos x 1
 1 2sin2 x 3 3 sin x 1 2sin x 
 3
 2sin2 x 2 3 sin x 3 0 sin x hoặc sin x 1 .
 2
 3 2 
Với sin x sin x sin x k2 hoặc x k2 , k Z 
 2 3 3 3
Với sin x 1 x k2 , k Z 
 2
 2 
So với điều kiện nghiệm của phương trình: x k2 ; x k2 , k Z . 
 3 2
 2 3 sin 2x 1 cos 2x 4cos 2x.sin2 x 3
7). 0 
 2sin 2x 1
 LỜI GIẢI
 2x k2 x k 
 1 6 12
Điều kiện: 2sin 2x 1 0 sin 2x , k Z . 
 2 5 5 
 2x k2 x k 
 6 12
 2 3 sin 2x 2 3 sin 2xcos 2x 2cos 2x 1 cos 2x 3 0 
 2 3 sin 2x 2cos 2x 3 sin 4x 2cos2 2x 3 0 
 2 3 sin 2x 2cos 2x 3 sin 4x 1 cos 4x 3 0 
 2 3 sin 2x cos 2x 3 sin 4x cos 4x 2 0 
 3 1 3 1
 2 sin 2x cos 2x sin 4x cos 4x 1 0 
 2 2 2 2
 2 sin 2x.cos cos 2x.sin sin 4x.sin cos 4x.cos 1 0 
 6 6 3 3 
 2sin 2x cos 4x 1 0 
 6 3 
 Ta có 4x 2 2x áp dụng công thức nhân đôi, ta được: 
 3 6 
 2 
 2sin 2x 1 2sin 2x 1 0 
 6 6 
 2sin 2x 1 sin 2x 0 sin 2x 0  sin 2x 1 
 6 6 6 6 
 7 
Với sin 2x 0 x k hoặc x k , k Z 
 6 12 12
 Với sin 2x 1 2x k2 x k k Z . 
 6 6 2 3
 7 
So với điều kiện nghiệm của phương trình: x k ; x k , k Z . 
 12 3
 (1 cos 2x)2
8). sin2 x 2cos 2x 
 2sin 2x
Điều kiện sin 2x 0 
 4cos4 x
 1 cos2 x 2(2cos2 x 1) cot x.cos2 x 5cos2 x 3 
 4sin x.cos x
Chia hai vế cho cos2 x ( dựa vào điều kiện cos x 0 )
 1 3 1
 5 5 3(1 tan2 x) 3tan3 x 2 tan x 1 0 
 tan x cos2 x tan x
 tan x 1 x k (k ¢ ) 
 4
So với điều kiện nghiệm của phương trình x k (k ¢ ) 
 4
Câu : Giải các phương trình sau:
 1 cos x 7 
1). sin x 2 sin 2x 
 tan x 4 
 (4sin2 x 1)cos x 2sin x(2cos x 3) 3
2). 2 3 sin2 x cos x 
 2sin x 1
 2sin x 7 
3). 2 sin x 1 
 x 4
 1 tan x.tan 
 2
 tan x.cos 3x 2cos 2x 1
4). 3(sin 2x cos x) 
 1 2sin x
 2(1 cot 2x.cot x) 1
5). 48 
 sin2 x cos4 x
 sin 3x cos x tan2 x 2 tan x 1 
6). 2 2 
 cos 2x 1 tan x sin 2x 3 cos 2x 3 sin x cos x 3
7). 1 
 2sin x 1
 sin x 1
8). cot x 2 
 1 cos x 1 cos x
 sin 2x cos 2x 4 2 sin x 3cos x
 4 
9). 1 
 cos x 1
 1 2sin x 1 sin x
10). 
 1 2sin x 3 cos x
 LỜI GIẢI
 1 cos x 7 
1). sin x 2 sin 2x (1)
 tan x 4 
 cos x 0 x k 
Điều kiện 2 
 tan x 0 
 x k 
 7 
Ta có : sin 2x sin 2x 2 sin 2x 
 4 4 4 
 (1 cos x).cos x 
 (1) sin x 2 sin 2x 
 sin x 4 
Có 2 sin 2x sin 2x cos 2x , và quy đồng mẫu được:
 4 
 (1 cos x).cos x sin2 x (sin 2x cos 2x).sin x 
 cos x cos2 x sin2 x sin 2x.sin x cos 2x.sin x 
Biến đổi cos2 x sin2 x cos 2x và sin 2x.sin x 2sin2 x.cos x được:
 cos x cos 2x 2sin2 x.cos x cos 2x.sin x 
 (cos x 2sin2 x.cos x) cos 2x cos 2x.sin x 0 
 cos x(1 2sin2 x) cos 2x cos 2x.sin x 0 
 cos x.cos 2x cos 2x cos 2x.sin x 0 
 cos 2x 0
 cos 2x(cos x sin x 1) 0 
 cos x sin x 1 0
 k 
 Với cos 2x 0 2x k x (k ¢ ) 
 2 4 2
 Với cos x sin x 1 x k2 hoặc x k2 ,(k ¢ )
 2
Biểu diễn nghiệm : π
 3π * 2
 π
 4
 4
 π 0
 5π 7π
 4
 3π 4
 2
 3 
Nghiệm x k được biểu diễn hai đầu mút là và .
 2 2 2
Nghiệm x k được biểu diễn hai đầu mút là 0 và .
 3 
Vậy ta phải bỏ 4 đầu mút 0, , , .
 2 2
Nghiệm x k2 được biểu diễn 1 đầu mút là .
 2 2
Nghiệm x k2 được biểu diễn 1 đầu mút là 0 .
 k 3 5 7 
Nghiệm x được biểu diễn 4 đầu mút là : , , , .
 4 2 4 4 4 4
So với điều kiện hai nghiệm x k2 và x k2 loại.
 2
 k 
Kết luận nghiệm của phương trình : x (k ¢ ) 
 4 2
 (4sin2 x 1)cos x 2sin x(2cos x 3) 3
2). 2 3 sin2 x cos x 
 2sin x 1
 4sin2 x.cos x cos x 4sin xcos x 2 3 sin x 3
 2 3 sin2 x cos x
 2sin x 1 
 cos x(4sin2 x 4sin x 1) 3(2sin x 1)
 2 3 sin2 x cos x
 2sin x 1 
 cos x(2sin x 1)2 3(2sin x 1)
 2 3 sin2 x cos x
 2sin x 1 
 cos x(2sin x 1) 3 2 3 sin2 x cos x
 2
 2sin xcos x cos x 3(1 2sin 2x) cos x 
 1 3
 sin 2x 3 cos 2x 0 sin 2x cos 2x 0
 2 2 
 k 
 sin 2x 0 x (k ¢ ) 
 3 6 2 
 x k2 
 1 6
Điều kiện : 2sin x 1 0 sin x (k ¢ ) 
 2 7 
 x k2 
 6
Biểu diễn nghiệm trên vòng tròn lượng lượng giác:
 π
 2
 2π π
 3 6
 π 0
 7π π 5π
 -
 6 6 3
 k 2 7 5 
Nghiệm x được biểu diễn 4 đầu mút , , , .
 6 2 6 3 6 3
 5 
Ta có đầu mút và trùng nhau.
 6 3
 2 
So với điều kiện ta chọn 2 đầu mút , .
 6 3
 2 
Vậy nghiệm của phương trình x k2 ,x k2 , k ¢ 
 6 3
 2sin x 7 
3). 2 sin x 1 (1)
 x 4
 1 tan x.tan 
 2
 cos x 0 
 x k 
Điều kiện x 2 , k ¢ .
 cos 0 
 2 x k2 
 7 
Ta có : 2 sin x 2 sin x 2 2 sin x sin x cos x . 
 4 4 4 
 x x x x 
 sin .sin x cos x.cos sin x.sin cos 
 x 2 1
Và 1 tan x.tan 1 2 2 2 
 2 x x x cos x
 cos .cos x cos x.cos cos x.cos
 2 2 2
 (1) 2sin x.cos x sin x cos x 1 (1') 
 t2 1
Đặt t sin x cos x sin x.cos x . Điều kiện t 2 
 2
 (1') t2 1 t 1 t2 t 2 0 t 1 t 2 (loại). 
 x k2 
 4 4 x k2 
 Với t 1 2 sin x 1 2
 4 
 x k2 x k2 
 4 4
So với điều kiện hai nghiệm này đều không thỏa.
Vậy phương trình vô nghiệm.
 tan x.cos 3x 2cos 2x 1
4). 3(sin 2x cos x) (1)
 1 2sin x
 x k2 
 1 6
Điều kiện : 1 2sin x 0 sin x 
 2 5 
 x k2 
 6
Ý tưởng quy đồng mẫu, sau đó đổi tanx bằng sinx chia cosx rồi quy đồng mẫu...
 tan x.cos 3x 2cos 2x 1 3(2sin x.cos x cos x)(1 2sin x)
 sin x.cos 3x 2cos 2x.cos x cos x 3 cos x(2sin x 1)(1 2sin x) 
 sin x.cos 3x 2cos 2x.cos x cos x 3 cos2 x(1 4sin2 x) 
 sin x.cos 3x 2cos 2x.cos x cos x 3 cos2 x(4cos2 x 3) 
 sin x.cos 3x 2cos 2x.cos x cos x 3 cos x(4cos3 x 3cos x) 
 sin x.cos 3x cos 3x cos x cos x 3 cos x.cos 3x 
 cos 3x(sin x 1 3 cos x) 0 
 cos 3x 0  sin x 3 cos x 1 
 k 
 Với cos 3x 0 3x k x (k ¢ ) 
 2 6 3
 1
 Với sin x 3 cos x 1 sin x 
 3 2
 3 
 sin x sin x k2 x k2 ,(k ¢ )
 3 6 6 2
Biểu diễn nghiệm trên vòng tròn lượng giác:
 π
 2
 5π π
 6 6
 7π
 11π
 6
 6
 3π
 2