Chuyên đề Giải tích Lớp 11 - Chương 4 - Bài 7: Giới hạn hàm số lượng giác (Có lời giải)

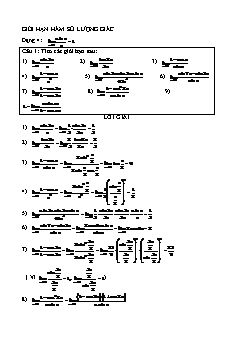
 GIỚI HẠN HÀM SỐ LƯỢNG GIÁC
 sin x
Dạng 4: lim 1
 x 0 x
Câu 1: Tìm các giới hạn sau: 
 sin 5x tan 2x 1 cos x
1). lim 2). lim 3). lim 
 x 0 x x 0 3x x 0 sin x
 1 cos x sin 5x.sin 3x.sin x sin7x sin 5x
4). lim 5). lim 6). lim
 x 0 x2 x 0 45x3 x 0 sin x
 1 cos 5x 1 cos2 2x
7). lim 8). lim 9). 
 x 0 1 cos 3x x 0 x.sin x
 x.sinax
L lim
 x 0 1 cosax
 LỜI GIẢI
 sin 5x 1 sin 5x 1
1). lim lim  
 x 0 x x 0 5 5x 5
 tan 2x 2 tan 2x 2
2). lim lim  
 x 0 3x x 0 3 2x 3
 x
 2sin2
 1 cos x x
3). lim lim 2 lim tan 0
 x 0 sin x x 0 x x x 0 2
 2sin cos
 2 2
 2
 x x 
 2sin2 sin
 1 cos x 1 1
4). lim lim 2 lim 2 
 x 0 x2 x 0 x2 x 0 2 x 2
 2 
 sin 5x.sin 3x.sin x 1 sin 5x sin 3x sin x 1
5). lim lim    
 x 0 45x3 x 0 3 5x 3x x 3
 sin7x sin 5x 2cos6xsin x
6). lim lim lim 2cos6x 2
 x 0 sin x x 0 sin x x 0
 2 2
 5x 5x 3x 
 2sin2 sin
 1 cos 5x 25 25
7). lim lim 2 lim  2  2 
 x 0 x 0 x 0
 1 cos 3x 2 3x 9 5x 3x 9
 2sin sin 
 2 2 2 
 5x 3x
 sin
 ( Vì lim 2 1, lim 2 1)
 x 0 5x x 0 3x
 sin
 2 2
 1 cos2 2x 1 cos 2x 1 cos 2x 
8). lim lim
 x 0 x.sin x x 0 x.sin x 2
 2sin x 1 cos 2x sin x
 lim lim 2 1 cos 2x 4
 x 0 x.sin x x 0 x
 ax ax ax ax
 x.2sin cos cos
 x.sinax x ax
9). L lim lim 2 2 lim cos lim 2  2
 x 0 x 0 x 0 x 0
 1 cosax 2 ax ax 2 ax a
 2sin sin sin
 2 2 2 2
 ax ax
 cos
 2 2
(Vì lim 2 1 và lim 2 ). Vậy L .
 x 0 ax x 0 a a a
 sin
 2 2
Câu 2: Tìm các giới hạn sau: 
 1 cosax sin x.sin 2x....sin nx 1 cosax
1). lim 2). lim 3). lim (a 0)
 x 0 1 cos bx x 0 n!xn x 0 x2
 sin x tan x tan x sin x sin x sina
4). lim 5). lim 6). lim
 x 0 x3 x 0 sin3 x x a x a
 cos x cos b 1 2x 1
7). lim 8). lim 9). 
 x b x b x 0 sin 2x
 cos(a x) cos(a x)
 lim
 x 0 x
 LỜI GIẢI
 ax ax bx 
 2sin2 sin
 1 cosax a 
1). L lim 2 lim  2  2 
 x 0 x 0
 1 cos bx 2 bx b ax bx
 2sin sin 
 2 2 2 
 ax bx
 sin
 a
Vì lim 2 1, lim 2 1. Vậy L 
 x 0 ax x 0 bx b
 sin
 2 2
2). 
 sin x.sin 2x....sin nx sin x.sin 2x....sin nx sin x sin 2x sin nx
 L lim lim lim  
 x 0 n!xn x 0 1.2.3....nxn x 0 x 2x nx
 sin x sin 2x sin nx
Vì lim 1, lim 1,, lim 1
 x 0 x x 0 2x x 0 nx
Vậy L 1.
 2
 2 ax ax ax
 2sin 2 sin sin
 1 cosax a 
3). L lim lim 2 lim 2 (vì lim 2 1 ).
 x 0 x2 x 0 x2 x 0 4 ax x 0 ax
 2 2
 a2
Vậy L .
 4 sin x
 sin x 
 sin x tan x sin x cos x 1 
4). L lim lim cos x 
 x 0 x3 x 0 x3 x3 cos x
 2
 x x 
 2sin2 sin x sin
 sin x 1
 lim 2 lim 2  
 x 0 x3 cos x x 0 x x 2cos x
 2 
 x
 sin
 sin x 1 1
Vì lim 2 1, lim 1, lim .
 x 0 x x 0 x x 0 2cos x 2
 2
 1
Vậy L 
 2
 sin x x
 sin x 2sin2
 tan x sin x 1 cos x
5). lim lim cos x lim lim 2 
 x 0 sin3 x x 0 sin3 x x 0 cos xsin2 x x 0 cos xsin2 x
 2
 x 
 sin
 1 
 . 2 
 2 x
 2 1
 lim 2
 x 0 sin x 2
 cos x. 
 x 
 x a x a x a
 2sin sin sin
 sin x sina x a
6). lim lim 2 2 lim sin  2 sina
 x a x a x a x a x a 2 x a
 2
 x b x b x b
 2sin sin sin
 cos x cos b 2 2 x b 2
7). lim lim lim sin . sin b
 x b x b x b x b x b 2 x b
 2
 1 2x 1 2x 1 1
8). lim lim  
 x 0 sin 2x x 0 sin 2x 1 2x 1 2
 cos(a x) cos(a x) 2sina sin x sin x
9). L lim lim lim .( 2sina)
 x 0 x x 0 x x 0 x
 sin x
 (Vì lim 1 ). Vậy L 2sina
 x 0 x
Câu 2: Tìm các giới hạn sau: 
 tan x tan c 1 cos3 x sin2 x sin2 a
1). lim 2). lim 3). lim
 x c x c x 0 xsin x x a x2 a2 cos x cosx sin 5x sin 3x x
4). lim 5). lim 6). lim 1 x tan 
 x 0 x2 x 0 sin x x 1 2
 x3 8 1 cos x.cos 2x.cos 3x
7). lim 8). lim
 x 2 tan(x 2) x 0 1 cos x
 sin a 2x 2sin a x sina tan a 2x 2 tan a x tana
9). lim 10) lim 
 x 0 x2 x 0 x2
 LỜI GIẢI
 tan x tan c sin(x c) 1 1 sin(x c)
1). lim lim  (vì lim 1 ).
 x c x c x c x c cos xcosc cos2 c x c x c
 2
 1 cos3 x 1 cos x 1 cos x cos x 
2). lim lim
 x 0 xsin x x 0 xsin x
 2 x x
 2sin sin 2
 1 cos x cos x 3
 lim 2 1 cos x cos2 x lim 2 . .
 x 0 x x x 0 x x 2
 x.2sin cos 2cos
 2 2 2 2
 sin2 x sin2 a sin x sina sin x sina 
3). lim lim
 x a x2 a2 x a x a x a 
 x a x a x a x a
 2cos sin sin cos sin x sina
 sin x sina 
 lim 2 2  lim 2  2
 x a x a x a x a x a x a
 2.
 2 2
 2cosa.sina sin 2a
 .
 2a 2a
 x( ) x( )
 2sin sin
 cos x cosx
4). lim lim 2 2 
 x 0 x2 x 0 x2
 x( ) x( )
 sin sin 2 2
 ( ) ( )  
 lim 2 lim 2 .lim ( 2) . 
 x 0 x( ) x 0 x( ) x 0 2 2 2
 2 2
 sin 5x sin 3x 2cos 4xsin x
5). lim lim lim(2cos 4x) 2
 x 0 sin x x 0 sin x x 0
 x
6). L lim 1 x tan . Đặt t x 1 , vì x 1 t 0
 x 1 2
 L lim( t)tan t 1 lim( t)tan t lim t cot t
 t 0 2 t 0 2 2 t 0 2 
 cos t t cos t
 2
 lim t. 2 lim 2  2 
 t 0 t 0 
 sin t sin t
 2 2 2
 2
 x3 8 x 2 x 2x 4 x 2
7). lim lim lim x2 2x 4 12
 x 2 tan(x 2) x 2 tan(x 2) x 2 tan(x 2)
 x 2
( Vì lim 1 ).
 x 2 tan(x 2)
 1 cos x.cos 2x.cos 3x
8). lim
 x 0 1 cos x
 1 cos x. cos 2x.cos 3x 1 cos 2x cos 3x 1 cos 3x 
 lim
 x 0 1 cos x
 1 cos x. cos 2x.cos 3x 1 cos 2x cos 3x 1 cos 3x
 lim lim lim 
 x 0 1 cos x x 0 1 cos x x 0 1 cos x
 2 3x
 2 2sin
 2sin xcos 3x
 lim cos 2x.cos 3x lim lim 2
 x 0 x 0 x x 0 x
 2sin2 2sin2
 2 2
 2
 3x 
 sin 
 2 
 x x 3x
 4sin2 cos2 cos 3x 
 1 lim 2 2 lim 9. 2 1 4 9 14
 x 0 x x 0 2
 sin2 x 
 2 sin 
 2 
 x 
 2 
 sin a 2x 2sin a x sina
9). lim
 x 0 x2
 sin a 2x sin a x sina sin a x 
 lim
 x 0 x2
 3x x x x
 2cos a sin 2cos a sin
 2 2 2 2
 lim
 x 0 x2
 x 3x x x x
 2sin cos a cos a 4sin sin a x sin
 2 2 2 
 lim lim 2 2
 x 0 x2 x 0 x2
 2
 x 
 sin 
 lim 1 2 sin a x sina
 x 0 x
 2 tan a 2x 2 tan a x tana
10). lim 
 x 0 x2
 tan a 2x tan a x tan a x tana 
 lim
 x 0 x2
 sin x sin x
 cos(a 2x)cos(a x) cos(a x)cosa
 lim
 x 0 x2
 sin x cosa cos(a 2x) sin x 2sin xsin(a x) 
 lim lim 
 x 0 x2 cos(a 2x)cos(a x)cosa x 0 x2 cos(a 2x)cos(a x)cosa 
 2
 sin x 2sin(a x) 2sina
 lim .
 x 0 x cos(a 2x)cos(a x)cosa cos3 a
Câu 3: Tìm các giới hạn sau: 
 sinax tan bx cos 3x cos 5x.cos7x
1). lim (a b 0) 2). lim
 x 0 (a b)x x 0 x2
 cosax cos bx.coscx sin a x sin a x 
3). lim 4). lim
 x 0 x2 x 0 tan a x tan a x 
 2x 1 3 x2 1 sin2 2x sin x.sin 4x
5). lim 6). lim
 x 0 sin x x 0 x4
 1 cos 5x.cos7x 1 1 
7). lim 8). lim 
 x 0 sin2 11x x 0 sin x tan x 
 sin x sin 2x 1 x2 cos x
9). lim 10). lim
 x 0 x 0 2
 2 x x
 x 1 2sin 
 2 
 LỜI GIẢI 
 sin bx
 sinax 
 sinax tan bx sinax sin bx
1). lim lim cos bx lim lim
 x 0 (a b)x x 0 (a b)x x 0 (a b)x x 0 (a b)x.cos bx
 a sinax b sin bx a b
 lim  lim  1
 x 0 a b ax x 0 (a b)cos bx bx a b a b
 cos 3x cos 5x.cos7x cos 3x 1 1 cos 5x cos7x 1 cos7x
2). lim lim
 x 0 x2 x 0 x2
 cos 3x 1 1 cos 5x cos7x 1 cos7x
 lim lim lim
 x 0 x2 x 0 x2 x 0 x2
 3x 5x 7x
 2sin2 2sin2 cos7x 2sin2
 lim 2 lim 2 lim 2
 x 0 x2 x 0 x2 x 0 x2 2 2 2
 3x 5x 7x 
 sin sin sin
 9 25cos7x 49 9 25 49 65
 lim . 2 lim 2 lim 2 
 x 0 2 3x x 0 2 5x x 0 2 7x 2 2 2 2
 2 2 2 
 cosax cos bx.coscx cosax 1 cos bx 1 coscx 1 coscx
3). lim lim
 x 0 x2 x 0 x2
 ax bx cx
 2sin2 2sin2 coscx 2sin2
 lim 2 lim 2 lim 2
 x 0 x2 x 0 x2 x 0 x2
 2 2 2
 ax bx cx 
 2 sin 2 sin 2 sin 2 2 2
 a b coscx c a b c
 lim 2 lim  2 lim  2 
 x 0 2 ax x 0 2 bx x 0 2 cx 2
 2 2 2 
 sin a x sin a x 2cosa sin x
4). lim lim
 x 0 tan a x tan a x x 0 sin 2x
 cos(a x)cos(a x)
 cosa cos(a x)cos(a x)
 lim cos3 a
 x 0 cos x
 2x 1 3 x2 1
5). lim 
 x 0 sin x
 2x 1 1 1 3 x2 1 2x 1 1 1 3 x2 1
 lim lim lim
 x 0 sin x x 0 sin x x 0 sin x
 2x x2
 lim lim
 x 0 x 0 2
 sin x 2x 1 1 3 2 3 2 
 sin x 1 x 1 x 1 
 x 2 x x 2
 lim  lim  0 1
 x 0 x 0 2
 sin x sin x 3 3 1 1
 2x 1 1 1 x2 1 x2 1 
 sin2 2x sin x.sin 4x sin2 2x 2sin xsin 2xcos 2x
6). lim lim
 x 0 x4 x 0 x4
 sin 2x 2sin xcos x 2sin xcos 2x 
 lim
 x 0 x4
 3x x
 2sin 2x.sin x cos x cos 2x 4sin 2x.sin x.sin .sin
 lim lim 2 2
 x 0 x4 x 0 x4
 3x x 
 sin sin 
 sin 2x sin x 2 2
 lim 6     6
 x 0 2x x 3x x
 2 2 1 cos 5x.cos7x
7). lim
 x 0 sin2 11x
 2 5x 2 7x
 1 cos 5x cos7x 1 cos7x 2sin cos7x 2sin
 lim lim 2 lim 2
 x 0 sin2 11x x 0 sin2 11x x 0 sin2 11x
 2 2
 5x 7x 
 sin sin 
 2 cos7x 2 
 5x 7x
 25 49 25 49 37
 2  2  
 lim 2 lim 2
 x 0 sin11x 484 x 0 sin11x 484 484 484 242
 11x 11x 
 x
 2sin2
 1 1 1 cos x 1 cos x 2
8). lim lim lim lim
 x 0 sin x tan x x 0 sin x sin x x 0 sin x x 0 x x
 2sin cos
 2 2
 x
 lim tan 0 .
 x 0 2
 3x x x 3x
 2cos sin sin cos
 sin x sin 2x
9). lim lim 2 2 lim 2  2 1
 x 0 x 0 x 0
 2 x xcos x x cos x
 x 1 2sin 
 2 2
 1 x2 cos x 1 x2 1 1 cos x 1 x2 1 1 cos x
10). lim lim lim lim
 x 0 x2 x 0 x2 x 0 x2 x 0 x2
 2
 2 x x 
 2 2sin sin
 x 1 1 1 1
 2  2 .
 lim lim 2 lim lim 1
 x 0 2 2 x 0 x x 0 2 x 0 2 x 2 2
 x 1 x 1 1 x 1 
 2 
Câu 3: Tìm các giới hạn sau: 
 1 tan x 1 sin x x 3 2
1). lim tan 2x.tan x 2). lim 3). lim
 x 0 3 x 1
 x 4 x tan(x 1)
 4
 cos x 1 cos x
4). lim 5). lim 6). 
 x 2
 x 
 2 x x 
 2
 sin(x 1)
 lim
 x 1 x2 4x 3 2sin x 1 2 sin x 1
7). lim 8). lim 9). 
 2 2
 x 4cos x 3 x 2cos x 1
 6 4
 sin x 
 6 
 lim
 x 1 2sin x
 6
 LỜI GIẢI
1). L lim tan 2x.tan x . Đặt t x , vì x t 0
 x 4 4 4
 4
 L lim tan 2t ( 1)tan t lim cot 2t.tan t 
 t 0 2 t 0
 cos 2t sin t cos 2t sin t cos 2t 1
 lim lim lim 
 t 0 sin 2t cos t t 0 2sin t cos t cos t t 0 2cos2 t 2
 1 tan x 1 sin x tan x sin x sin x x cos x 
2). lim lim lim
 x 0 x3 x 0 x 0 x3 .A.cos x
 3 
 x 1tanx1sinx 
 A 
 2
 2 x x 
 2sin xsin sin 
 2 sin x 2 1 1
 lim lim . . .
 x 0 x3 .A.cos x x 0 x x 2A.cos x 4
 2 
 x 3 2 x 3 4 x 1 1
3). lim lim lim
 x 1 tan(x 1) x 1 x 3 2 tan(x 1) x 1 tan(x 1) x 3 2
 x 1 1 1
(Vì lim 1, lim )
 x 1 tan(x 1) x 1 x 3 2 4
 1
Vậy L .
 4
 cos x 
4). L lim . Đặt t x , vì x t 0
 x 2 2
 2 x 
 2
 cos t 
 2 sin t
 L lim lim 1 .
 t 0 t t 0 t
 1 cos x
5). . Đặt , vì 
 L lim 2 t x x t 0
 x x 2
 t t 
 2sin2 sin
 1 cos(t ) 1 cos t 1 1
 L lim lim lim 2 lim 2 .
 t 0 t2 t 0 t2 t 0 t2 t 0 2 t 2
 2 
 sin(x 1) sin(x 1)
6). L lim lim . Đặt t x 1 , vì x 1 t 0
 x 1 x2 4x 3 x 1 x 1 x 3 
 sin t sin t 1 1
 L lim lim  .
 t 0 t.(t 2) t 0 t t 2 2
 2sin x 1 2sin x 1 2sin x 1
7). L lim lim lim
 2 2 2
 x 4cos x 3 x 4 1 sin x 3 x 1 4sin x
 6 6 6
 2sin x 1 1 1
 lim lim 
 x 1 2sin x 1 2sin x x 1 2sin x 2
 6 6
 2 sin x 1 2 sin x 1 2 sin x 1
8). L lim lim lim
 2 2 2
 x 2cos x 1 x 2 1 sin x 1 x 1 2sin x
 4 4 4
 2 sin x 1 1 1
 lim lim .
 x x 1 2 sin x 2
 4 1 2 sin x 1 2 sin x 4
 sin x sin x sin x 
 6 6 6 
9). lim lim lim
 x 1 2sin x x 1 x 
 6 6 2 sin x 6 2 sin x sin 
 2 6 
 x x x 
 2sin cos cos 
 2 12 2 12 1 2 12 3
 lim lim 
 x x x x 2 x 3
 6 4cos sin 6 cos 
 2 12 2 12 2 12 
Câu 4: Tìm các giới hạn sau: 
 sin x 
 1 2sin x 4 2 2cos x
1). lim 2). lim 3). lim
 x x 1 2 sin x x 
 6 x 4 4 sin x 
 6 4 
 x2 1 cos 2x 1 2x cos x x 3 2x 1 1 x
4). lim 5). lim 6). lim
 x 0 x2 x 0 x2 x 0 sin 2x
 sin x 3 cos x 1 cos x cos 2x 1 3 cos x
7). lim 8). lim 9). lim
 x 0 2 x 0 2
 x sin 3x x tan x
 3
 LỜI GIẢI