Chuyên đề Giải tích Lớp 11 - Chương 4 - Bài 3, Phần 2: Giới hạn hàm số lý thuyết và phương pháp giải toán (Có lời giải)

 DẠNG 4: Các giới hạn đặc biệt
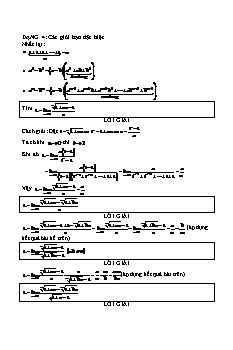
Nhắc lại:
 1 1 1  1 n 
 n
 a3 b3 a b a2 ab b3 
  
 3 so hang 
 an bn a b an 1 an 2b an 3b2  abn 2 bn 1 
  
 n so hang 
 n 1 ax 1
Tìm L lim
 x 0 x
 LỜI GIẢI
 tn 1
Cách giải: Đặt t n 1 ax tn 1 ax x 
 a
Ta có khi x 0 thì t 1 .
 a t 1 
Khi đó L lim
 x 1 tn 1
 a t 1 a a
 lim lim 
 x 1 t 1 tn 1 tn 2  t 1 x 1 tn 1 tn 2  t 1 n
 n 1 ax 1 a
Vậy L lim 
 x 0 x n
 n 1 ax m 1 bx
 L lim
 x 0 x
 LỜI GIẢI
 n 1 ax 1 1 m 1 bx n 1 ax 1 m 1 bx 1 a b
 L lim lim lim (áp dụng 
 x 0 x x 0 x x 0 x n m
kết quả bài kế trên).
 n 1 ax 1
 L lim ab 0 
 x 0 m 1 bx 1
 LỜI GIẢI
 n 1 ax 1 x a m am
 L lim   (áp dụng kết quả bài trên).
 x 0 x m 1 bx 1 n b bn
 n 1 ax m 1 bx
 L lim
 x 0 1 x 1
 LỜI GIẢI n 1 ax 1 1 m 1 bx x n 1 ax 1 m 1 bx 1 
 L lim  lim 1 x 1
 x 0 x 0 
 x 1 x 1 x x 
 a b 
 2 
 n m 
 m x 1
 L lim
 x 1 n x 1
 LỜI GIẢI
Đặt t mn x x tmn , vậy m x tn , n x tm
 n 1 n 2
 tn 1 t 1 t t  t 1 tn 1 tn 2  t 1 n
 L lim lim lim .
 t 1 tm 1 t 1 t 1 tm 1 tm 2  t 1 t 1 tm 1 tm 2  t 1 m
 x x2 x3  xn n
 L lim
 x 1 x x2 x3  xm m
 LỜI GIẢI
Ta có: x x2 x3  xn n x 1 x2 1 x3 1  xn 1 
 x 1 x 1 x 1 x 1 x2 x 1  x 1 xn 1 xn 1  1 
 2  n 1 n 1  
 x 1 1 x 1 x x 1 x x 1 
Tương tự: : x x2 x3  xm m x 1 x2 1 x3 1  xm 1 
 x 1 x 1 x 1 x 1 x2 x 1  x 1 xm 1 xm 1  1 
 2  m 1 m 1  
 x 1 1 x 1 x x 1 x x 1 
 2  n 1 n 1  
 x 1 1 x 1 x x 1 x x 1 
Vậy L lim
 x 1 2  m 1 m 1  
 x 1 1 x 1 x x 1 x x 1 
 1 x 1 x2 x 1  xn 1 xn 1  1 
 lim
 x 1 1 x 1 x2 x 1  xm 1 xm 1  1 
 n(n 1)
 1 2 3  n n(n 1)
 2 .
 1 2 3  m m(m 1) m(m 1)
 2
 x100 2x 1
 L lim
 x 1 x50 2x 1
 LỜI GIẢI
 100 99
 x100 x x 1 x x x 1 x x 1 x 1 
 L lim lim lim
 x 1 x50 x x 1 x 1 x50 x x 1 x 1 x x49 1 x 1 x x 1 x98 x97  x 1 x 1 x 1 x99 x98  x2 x 1 
 lim lim
 x 1 x x 1 x48 x47  x 1 x 1 x 1 x 1 x49 x48  x2 x 1 
 x99 x98  x2 x 1 98 49
 lim 
 x 1 x49 x48  x2 x 1 48 24
 xn 1 n 1 x n
 L lim 2
 x 1 x 1 
LỜI GIẢI
Ta có xn 1 n 1 x n xn 1 x nx n x xn 1 n x 1 
 x x 1 xn 1 xn 1  x 1 n x 1 x 1 xn xn 1  x2 x n 
 x 1 xn xn 1  x2 x 1 1 1  1 
   
 n so hang n so hang 
 n n 1 2 
 x 1 x 1 x 1 x 1 x 1 
 x 1 x 1 xn 1 xn 2  1 x 1 xn 2 xn 3  1  x 1 x 1 x 1 
   
  n   n 1  
 n 
 2 
 x 1 xn 1 xn 2  1 xn 2 xn 3  1  x 1 1 
   
 n   n 1   
 n 
 2 n 1 n 2 n 2 n 3 
 x 1 x x  1 x x  1  x 1 1 
 n n 1 
  
Do đó: n 
 L lim 2
 x 1 x 1 
 L lim xn 1 xn 2  1 xn 2 xn 3  1  x 1 1 
 x 1  
 n n 1 
  
 n 
 n n 1 
 n (n 1)  2 1 
 2
 m n 
 lim , m,n ¥ * 
 x 1 1 xm 1 xn 
 LỜI GIẢI m 1 n 1 m 1 n 1 
 lim m n lim m lim n 
 x 1 1 x 1 x 1 x 1 x x 1 1 x 1 x x 1 1 x 1 x 
 2 m 1
 m 1 m 1 x x  x 
 lim lim
 x 1 1 xm 1 x x 1 1 xm
 1 x 1 x2  1 xm 1 
 lim
 x 1 1 xm
  2  m 2 
 1 x 1 1 x 1 x x x 
 lim
 x 1 1 x 1 x x2  xm 1 
 2 m 2
 1 1 x  1 x x  x 1 2  m 1 m 1
 lim 
 x 1 1 x x2  xm 1 m 2
 n 1 n 1
Tương tự lim 
 x 1 1 xn 1 x 2
 m n m 1 n 1 m n
Vậy lim 
 x 1 1 xm 1 xn 2 2 2
Ví dụ: Tìm các giới hạn sau:
 3x 1 3 2 x 2 4 x 3 8 3x 4
a). lim b). lim 
 x 1 x 1 x 0 x2 x
 1.2x 1 3 2.3x 1 4 3.4x 1 1
c). lim
 x 0 x
LỜI GIẢI
 3 3
 3x 1 2 x 1 3x 1 2 3x 1 2 x 1 3x 1 2
a). lim lim lim
 x 1 x 1 x 1 x 1 x 1 x 1
 3
 3x 1 2 x 1 3x 1 2 x 1 
 Tính lim lim
 x 1 x 1 2
 x 1 3 3 
 x 1 2 x 2 x 1
 3x 1 2
 lim 
 x 1 2
 3 2 x 3 2 x 1 3
 3x 1 2 3x 1 4 3 3
 Tính lim lim lim .
 x 1 x 1 x 1 x 1 3x 1 2 x 1 3x 1 2 4
 3x 1 3 2 x 2 2 3 1
Vậy lim .
 x 1 x 1 3 4 12
b). 
 3 3 3
 8 3x 4 x 2 2 8 3x 4 8 3x 4 x 2 2 3 8 3x 4
 lim lim lim
 x 0 x2 x x 0 x2 x x 0 x2 x Tính 
 3
 8 3x 4 x 2 3 8 3x.x 3 8 3x 1
 lim 2 lim lim
 x 0 x x x 0 x x 1 4 x 2 x 0 x 1 4 x 2 2
 2 3 8 3x 4 8 3x 8
 Tính lim 2lim
 x 0 2 x 0 2
 x x 3 3 
 x x 1 8 3x 2 8 3x 4
 3 1
 2lim 
 x 0 2 2
 x 1 3 8 3x 2 3 8 3x 4
 4 x 3 8 3x 4 1 1
Vậy lim 1
 x 0 x2 x 2 2
 3 4
 1.2x 1 3 2.3x 1 4 3.4x 1 1 2x 1 1 2.3x 1 3.4x 1
c). L lim lim 
 x 0 x x 0 x
 3 4
 2.3x 1 1 3.4x 1 4 3.4x 1 1
 lim lim
 x 0 x x 0 x
 n ax 1 1 a
Ta chứng minh được lim a 0,n ¥ * 
 x 0 x n
GIỚI HẠN CỦA HÀM SỐ KHI x 
DẠNG 1: Tính giới hạn trực tiếp
Ví dụ: Tính giới các giới hạn sau:
a). lim(2x3 3x) b). lim x2 3x 4 c). lim 2x2 1 x
 x x x 
 LỜI GIẢI
 3 3 3 3
a). lim(2x 3x) lim x 2 lim 2x 
 x x x2 x 
 3 4 
 lim x 1 
 x 2 lim x 
 2 3 4 x x 
b). lim x 3x 4 lim x 1 x 
 2 
 x x x x lim x 
 3 4 x 
 lim x 1 
 x x x2
 2 2 1 1
c). lim 2x 1 x lim x 2 x lim x 2 x 
 x x 2 x 2 
 x x 
 1 
 lim x 2 x lim x 2 1 .
 x 2 x 
 x 
DẠNG 2: 
 PHƯƠNG PHÁP GIẢI TOÁN: Chia cả tử và mẫu cho xk là lũy thừa cao 
nhất của tử và mẩu (hoặc đặt xk làm nhân tử chung).
Ví dụ 1: Tìm giới hạn của các hàm số sau:
 2
 3x 2x 1 2x5 x3 1 x x 1
a). lim b). lim 3 c). lim 
 x 5x 1 x2 2x x 2x2 1 x3 x x x2 x 1
 2 x 3 2x3 x 2x4 x2 1
d). e). f). .
 L lim lim x. 5 2 lim
 x x2 x 5 x x x 3 x 1 2x
 LỜI GIẢI
 2 1 1 
 2 3x.x 2 3 2 
 3x 2x 1 x2 x2 3.2 6
a). lim lim lim .
 x 2 x x 
 5x 1 x 2x 1 2 2 1 2 5.1 5
 x 5 x 1 5 1 
 x x x x 
b). 
 5 1 1 1 1 
 x 2 2 
 2x5 x3 1 x2 x5 x2 x5 
 lim 3 lim 3 lim 3 1
 x 2 3 x x 
 2x 1 x x 2 1 3 1 1 1 
 x 2 x 1 2 1 
 x2 x2 x2 x2 
 1 1
 x x 1 
 x x 1 2 x2 0
c). lim lim x lim x 0 .
 x x2 x 1 x x2 x 1 x 1 1 1
 1 
 x2 x x2
 2 x 3
d). L lim
 x x2 x 5
 2x 3
vì x x 0 x x . Vậy L lim
 x x2 x 5
 3 3
 x 2 2 
 2x 3 2x 3 x 
 lim lim lim lim x 2
 x x 1 5 x 1 5 x 1 5
 2 1 5 
 x 1 x 1 2 x 1 2 1 2
 x x2 x x x x x x 3 1 1 
 x 2 2 
 2x3 x x2 x2 
e). lim x. lim x. lim x.
 x 5 2 x x 
 x x 3 5 1 3 2 1 3 
 x 1 x 1 
 x3 x5 x3 x5 
 1 1 
 2 2 
 x x2 x2 
 lim lim 2
 x x 1 3 x 1 3 
 1 1 
 x3 x5 x3 x5 
 4 1 1 
 x 2 
 2x4 x2 1 x2 x4 
f). lim lim
 x 1 2x x 1 2x
 1 1 1 1
 x2 2 x 2 
 2 4 2 4 2 
 lim x x lim x x lim x 
 x 1 2x x 1 x 2 
 2 
 x
Ví dụ 2: Tính các giới hạn sau:
 2
 x x x x x2 3x 2x
a). lim x 1 b). lim c). lim 
 x 2x4 x2 1 x x 10 x 3x 1
 x2 x 2 3x 1 x2 x 2 3x 1
d). lim e). lim 
 x 4x2 1 1 x x 4x2 1 1 x
 3 (x3 2x2 )2 x 3 x3 2x2 x2
f). lim
 x 3x2 2x
 LỜI GIẢI
 1 2 1
 2 
 x x x 1 2 3
a). lim x 1 lim lim x x x 0 . (Chú thích: 
 x 2x4 x2 1 x 2x4 x2 1 x 1 1
 2 
 x2 x4
Vì x nên x 0 (x 1) 0 do đó ta được được vào trong dấu căn.
 2 1 1 1
 2 x x 1 x x 1 x x 1 
 x x x x 
b). lim lim lim x lim x 
 x x 10 x x 10 x x 10 x x 10
 1
 1 1 
 lim x 2 . (Chú giải: Vì x nên x 0 do đó x x ).
 x 10
 1 
 x c). 
 2 3 3 3
 x 1 2x x 1 2x x 1 2x
 x2 3x 2x x 
 lim lim lim x lim x 
 x 3x 1 x 3x 1 x 3x 1 x 3x 1
 3
 1 2
 1 2 1
 lim x . (Chú giải: Vì x nên x 0 do đó x x ).
 x 1 3 3
 3 
 x
 x2 x 2 3x 1 x2 x 2 3x 1
 x2 x 2 3x 1
d). lim lim x lim x x x
 x 4x2 1 1 x x 4x2 1 1 x x 4x2 1 1 x
 x x x x
 x2 x 2 1 1 2 1
 3 1 3 
 2 x x 2 x 1 3
 lim x lim x 4 .
 x 4x2 1 1 x 1 1 2 1
 1 4 1
 x2 x x2 x
 x2 x 2 3x 1 x2 x 2 3x 1
 x2 x 2 3x 1
e). lim lim x lim x x x
 x 4x2 1 1 x x 4x2 1 1 x x 4x2 1 1 x
 x x x x
 x2 x 2 1 1 2 1
 3 1 3 
 2 x x 2 x 1 3 2
 lim x lim x 
 x 4x2 1 1 x 1 1 2 1 3
 1 4 1
 x2 x x2 x
 2
 3 2 3 2 2
 3 x 1 3 x 1 x
 3 (x3 2x2 )2 x 3 x3 2x2 x2 x x 
f). lim lim
 x 3x2 2x x 3x2 2x
 2 2
 3
 2 2 3 2 2 2 2 2 2 2
 3 x 1 3 x 1 x x .3 1 x .3 1 x
 x x x x
 lim lim
 x 3x2 2x x 3x2 2x
 2 
 2 2 2
 2 3 3 2 2
 x 1 1 1 3 3
 x x 1 1 1
 x x 1 1 1
 lim lim 1 .
 x x 
 2 2 2 3
 x 3 3 
 x x
Ví dụ 3: Tìm các giới hạn sau: 4 2 
 x 2 x 3 4x 1 2x 4
a). lim x2 3 b). lim 
 x x x x 4 x 
 x 2x 
 LỜI GIẢI
 1
a). Đặt x khi x thì y 0
 y
 1 2y 3 1 3y 1 2y (1 y) 3 1 3y (1 y) 
 I lim lim 
 y 0 2 y 0 2 2
 y y y 
 y2 y2 (y 3)
 lim 
 2
 y 0 y 1 2y (1 y) 2 3 2 3 2 
 y ( (1 3y) (1 y) 1 3y (1 y) ) 
 1 y 3
 lim 
 y 0 1 y 1 2y 2 3 3 2 
 (1 y) (1 y) 1 3y (1 3y) 
 1 1 1
 1 . Vậy I 
 2 2 2
 2 
 4 2x 4 
 4x 1 x2 
 4 2 2 
 4x 1 2x 4 4 x 
b). lim lim x 
 x x 2x4 x x x 2x4 x 
 x4
 1 4 1 4 1 
 4 x 2 4 x 2 4 
 4 x2 4 x2 4 4
 lim x lim x lim x 2 
 x 1 x x 1 x x 1 2 
 2 2 2 x
 3 3 3 
 x x x 
 2 2 2 2 .
DẠNG 3: 
PHƯƠNG PHÁP GIẢI TOÁN: Nhân lượng liên hợp sau đó làm như dạng 
1.
Ví dụ: Tìm các giới hạn sau:
a). lim ( x2 x x) b). lim( x2 3x 2 x) c). lim ( x2 x x) 
 x x x 
d). lim( x2 3x 2 x) e). lim( x 2 x 2) 
 x x f). lim x2 4x 3 x2 3x 2 g). lim x2 4x 3 x2 3x 2
 x x 
 LỜI GIẢI
 2 2 1 1
a). lim ( x x x) lim x 1 x lim x 1 x 
 x x x 
 x x 
 1 1 
 lim x 1 x lim x 1 1 . Chú giải: Vì x nên x 0 
 x x 
 x x 
do đó x x . 
 x2 3x 2 x2 3x 2
b). lim( x2 3x 2 x) lim lim
 x x 2 x 
 x 3x 2 x 2 3 2 
 x 1 x
 x x2 
 2
 3 
 3x 2 3x 2 3
 lim lim lim x .
 x 3 2 x 3 2 x 3 2 2
 x 1 x x 1 x 1 1
 x x2 x x2 x x2
Chú thích: Do x nên x 0 do đó x x
c). lim x2 x x 
 x 
 2
 2 2 2 2
 x x x x x x x x x x
 lim lim lim
 x x2 x x x x2 x x 1
 2 x 1 x
 x 2 x
 x x
 x x 1 1
 lim lim lim .
 x 1 x 1 x 1 2
 x 1 x 1 1
 x 1 1 
 x x x
Chú giải: Vì x nên x 0 do đó x x . 
 x2 3x 2 3 2 
d). L lim x2 3x 2 x lim x2 x lim x 1 x 
 x x 2 x x 2 
 x x 
 3 2 3 2 
 lim x 1 x lim x 1 1 .
 x 2 x 2 
 x x x x 
 3 2
Do x nên x 0 do đó x x . Có lim lim 0 nên 
 x x x x2
 3 2 
 lim 1 1 2 và lim x . Từ đó suy ra L . 
 x 2 
 x x x