Chuyên đề Giải tích Lớp 11 - Chương 4 - Bài 2: Bài tập giới hạn dãy số tổng hợp (Có lời giải)

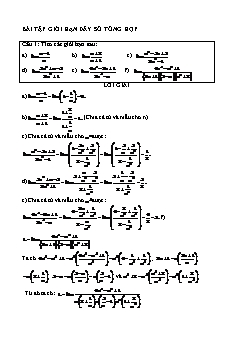
 BÀI TẬP GIỚI HẠN DÃY SỐ TỔNG HỢP 
Câu 1: Tìm các giới hạn sau:
 n 1 n 2 n2 3n 5
a). lim b). lim c). lim 
 n n 1 2n2 1
 3n2 n 5 6n3 2n 1 4n4 n2 1
d). lim e). lim f). lim .
 2n2 1 2n3 n 2n 1 3 n n2 2 
 LỜI GIẢI
 n 1 1 
a) lim lim 1 0. 
 n n 
 2
 1 
 n 2
b) lim lim n 1. (Chia cả tử và mẫu cho n)
 n 1 1
 1 
 n
c) Chia cả tử và mẫu cho n2 được: 
 3n 5 3 5 
 1 1 
 n2 3n 5 2 2 2 1
 lim lim n n lim n n .
 2n2 1 1 1 2
 2 2 
 n2 n2 
 n 5 1 5
 3 3 
 3n2 n 5 2 2 2 3
d) lim lim n n lim n n . 
 2n2 1 1 1 2
 2 2 
 n2 n2
e) Chia cả tử và mẫu cho n3 được: 
 2n 1 2 1 
 6 6 
 6n3 2n 1 3 3 2 3 6
 lim lim n n lim n n 3. f)
 2n3 n n 1 2
 2 2 
 n3 n2 
 4n4 n2 1
 L lim 
 2n 1 3 n n2 2 
 4n4 n2 1 1 1 2n 1 
Ta có 4n4 n2 1 n4 n4 4 ; 2n 1 n 
 4 2 4 
 n n n n 
 1 3 n 3 n2 2 2 
 n 2 ; 3 n n n 1 và n2 2 n2 n2 1 
 2 2 
 n n n n n 
 4n4 n2 1
 Từ đó ta có: L lim
 1 3 2 2 
 n 2 n 1 n 1 
 n n n2 4 1 1 1 1
 n 4 4 
 n2 n4 2 4 4
 lim lim n n 2. 
 4 1 3 1 1 3 1 2.1
 n 2 1 1 2 1 1 
 n n n2 n n n2 
Câu 2: Tìm các giới hạn sau:
 2 2
 n 2 n 1 2 
a). b). n 2 n 3 
 lim 2 lim
 n 1 2n 3 2n2 n n
 2n3 11n 1 2n n 1 n 3 
c). lim d). lim
 n2 2 n 1 n 2 
 LỜI GIẢI
 2 2
 2 2 2 1 2 1 
 2 2 n 1 n 1 1 1 
 n 2 n 1 n2 n n2 n 1
a). lim lim lim . 
 2 2 2 2
 n 1 2n 3 1 2 3 1 3 
 n 1 n 2 1 2 
 n n n n 
 2 n 3 2 3
 1 1 
 2 2 n2 1
b). lim n n lim n n . 
 n n 1 1 2
 2 2 
 n2 n2 n n n
 2n3 11n 1 11 1
 2 2 2 2n 2
c). lim n n n lim n n lim 2n . 
 n2 2 2
 1 
 n2 n2 n2
 2n n 1 n 3 
 n n n 
 2n n 1 n 3 n n n 
d). lim lim 
 n 1 n 2 n 1 n 2 
 n n 
 n n 
 1 3 1 3 
 n n 2 n 1 2 1 
 n n n n n n 2.1
 lim lim 2. 
 1 2 1 2 1.1
 n 1 n 1 1 1 
 n n n n 
Câu 3: Tìm các giới hạn sau:
 9n2 n 1 2n4 3n 2
a). lim b). lim 
 4n 2 2n2 n 3
 2n 2 n 3n2 1 n2 1
c). lim d). lim
 n n
 LỜI GIẢI 1 1 
 2 1 1 1 1
 n 9 2 n 9 9 
 9n2 n 1 n n n 2 n 2 3
a) lim lim lim n lim n . 
 4n 2 2 2 2 2
 n 4 n 4 4 
 n n n
 4 3 2 
 n 2 
 2n4 3n 2 n3 n4 
b). 
 lim 2 lim
 2n n 3 2 1 3 
 n 2 
 n n2 
 3 2 3 2
 n2 2 2 
 3 4 3 4 2
 lim n n lim n n . 
 1 3
 2 1 3 2
 n 2 2 2
 n n2 n n
 2 2
 n 2 n n 2 n
 2n 2 n n 
c). lim lim lim n 
 n n n
 2 
 n 2 1 
 n 2 
 lim lim 2 1 2 1.
 n n 
 2 1 2 1 
 n 3 n 1 
 3n2 1 n2 1 n2 n2 
d). lim lim 
 n n
 1 1 
 1 1 n 3 1 
 n 3 n 1 2 2 
 2 2 n n 
 lim n n lim 
 n n
 1 1 
 lim 3 1 3 1. 
 2 2 
 n n 
Câu 4: Tìm các giới hạn sau:
 3n 5.4n 3n 2.5n 2n 3n 5n 2 4.3n 5n 1
a). lim b). lim c). lim d). lim
 4n 2n 7 3.5n 2n 1 3n 2 5n 1 3.2n 5n
 LỜI GIẢI
 n
 3n 5.4n 3 
 5
 3n 5.4n n n 4 5
a). lim lim 4 4 lim 5. 
 4n 2n 4n 2n n 1
 2 
 n n 1 
 4 4 4 n
 3n 2.5n 3 
 2
 3n 2.5n n n 5 2
b). lim lim 5 5 lim . 
 7 3.5n 7 3.5n 7 3
 3
 5n 5n 5n
 2n 3n 5n 2 2n 3n 52.5n
c). lim lim 
 2n 1 3n 2 5n 1 2.2n 32.3n 5.5n
 n n
 2n 3n 52.5n 2 3 
 25
 n n n 5 5 
 lim 5 5 5 lim 5. 
 2.2n 32.3n 5.5n n n
 2 3 
 n n n 2. 9. 5
 5 5 5 5 5 
 n
 4.3n 5.5n 3 
 4. 5
 4.3n 5n 1 4.3n 5.5n n n 5 
d). lim lim lim 5 5 lim 5. 
 3.2n 5n 3.2n 5n 3.2n 5n n
 2 
 n n 3. 1
 5 5 5 
Câu 5: Tìm các giới hạn sau:
 n n 
 2n 5 n 1 .25n 1 2 
a). b). 9 1 c). d). n n 1
 lim n lim n lim 5n 2 lim n
 2.3n 3. 5 3 1 3 n.3
 LỜI GIẢI
 n
 2n 5 n
 2 
 n n n n 1
 2 5 5 5 5 1
a). lim lim lim . 
 n n n n
 2.3 3. 5 2.3n 3. 5 3 3
 2. 3
 n n 
 5 5 5 
 9n 1 1
 1 
 9n 1 n n
b). lim lim 3 lim 9 1. 
 3n 1 3n 1 1
 1 
 3n 3n
 n 5n 1 n 5n 5n
 1 .2 1 .2.2 1 .2 2 
c). lim lim lim . 0. 
 35n 2 32.35n 9 3 
 2 1
 n n 1 1 1 
 n n2 1 2 1 1 
d). L lim lim n lim n lim 1 1 . Có 
 n n n n 2 
 n.3 n.3 3 3 n 
 n
 1 1 1
 lim 0 nên lim 1 1 2 và lim 0. Do đó L 0 . 
 2 n n
 n n 3 Câu 6: Tìm các giới hạn sau:
 n2 4n 5 2n2 n 2 2n2 n sin 3n 
a). lim b). lim c). lim d). lim 1 
 3n3 n2 7 3n4 5 1 3n2 4n 
 LỜI GIẢI
 4 5
 1 
 n2 4n 5 2 1
a). lim lim n n lim 0. 
 3n3 n2 7 7 3n 1
 3n 1 
 n
 1 2
 2 
 2n2 n 2 2 2
b). n n 
 lim 4 lim lim 2 0.
 3n 5 2 5 3n
 3n 
 n2
 2n2 n 1
 2 
 2n2 n 2
c). lim lim n lim n lim 0. 
 1 3n2 1 1 3n
 3n 3n
 n n
 sin 3n sin 3n
d). lim 1 lim 1 
 4n 4n
 1 sin 3n 1
Ta có: 1 sin 3n 1 
 4n 4n 4n
 1 1 sin 3n sin 3n 
Mà: lim lim 0 lim 0. Vậy lim 1 1. 
 4n 4n 4n 4n 
 Câu 7: Tìm các giới hạn sau:
 n
 n n 5 4n
a). 1 b). 5 c). 3 5.4 d). 
 lim lim n n lim n n lim n 1
 3n 2 2n 1 4 2 7 2 7 4n 1
 LỜI GIẢI
 1 1
a). lim lim 
 3n 2 2n 1 2 1 
 n 3 n 2 
 n n 
 1 1
 lim lim 0. 
 2 1 n 3 2
 n 3 2 
 n n 
 1
 5. n n
 5 n 1 1 1 
b). lim lim 4 0. Do lim lim 0 và lim 0 . 
 n n n n 
 4 2 1 4 4 2 
 1 
 2 n
 3n 
 n 3 
 4 n 5 n 5 n
 3n 5.4n 4 4 4 3 
c). lim lim lim 0.Do lim 0 , 
 n n n n 
 7 2 n 2 7 2 4 
 7 1 
 n 1 
 7 7 
 n 
 3 
 n 5 n
 2 4 4 
 lim 0 nên lim 5 và lim 0 . Nên lim u 0 .
 n n
 7 2 7 
 1 
 7 
 n 
 n 4 n
 4 
 5 1 n
 n n n 1 
 5 4 5 5 5 
d). lim lim lim  . Do 
 n 1 n 
 n 1 n 7 
 7 4 n 4.4 4 
 7 7 7 4. 
 n 7 
 7 
 n 
 4 
 n n 1 n
 4 4 5 1 5 
 lim lim 0 nên lim và lim 0 .
 n 
 5 7 4 7 7 
 7 4. 
 7 
Từ đó suy ra lim un 0 . 
Câu 8: Tìm các giới hạn sau:
a). lim n2 n n b). lim n2 n 1 n 
c). lim 4n2 n 4n2 2 d). lim n n2 1 n2 2 
 LỜI GIẢI
 n2 n n2
a). lim n2 n n lim 
 n2 n n
 n n 1 1
 lim lim lim . 
 1 1 1 2
 2 1 1
 n 1 n n 1 1 
 n n n
 n2 n 1 n2
b). lim n2 n 1 n lim 
 n2 n 1 n
 1 1
 n 1 1 
 n 1 n 1
 lim lim lim n . 
 1 1 1 1 1 1 2
 n2 1 n n 1 1 1 1
 2 2 2
 n n n n n n 4n2 4n2 2 
c). lim 4n2 n 4n2 2 lim 
 4n2 n 4n2 2
 n 2 n 2
 lim lim 
 1 2
 2 1 2 2 
 n 4 n 4 n 4 n 4 2
 n n2 n n
 2 2
 n 1 1 
 n 1
 lim lim n . 
 1 2 1 2 4
 n 4 4 4 4 
 2 2
 n n n n
 n n2 1 n 2 
 2 2 
d). lim n n 1 n 2 lim 
 2 2
 n 1 n 2
 n n
 lim lim 
 1 2 1 2 
 n2 1 n2 1 n 1 1 
 2 2 2 2 
 n n n n 
 1 1 1
 lim lim . 
 1 2 1 1 2
 1 1 
 n2 n2
Câu 9: Tìm các giới hạn sau:
a). lim n2 2n n 3 b). lim 4n2 3n 1 2n 1 
c). lim 1 n2 n4 3n 1 d). lim n n 1 n .
 LỜI GIẢI
a). lim n2 2n n 3 lim n2 2n n 3 
 n2 2n n2 2n
 lim 3 lim 3 
 2
 n 2n n 2 2 
 n 1 n
 n 
 2n 2 2
 lim 3 lim 3 3 4. 
 2 2 1 1
 1 1
 n 1 1 
 n n
b). lim 4n2 3n 1 2n 1 lim 4n2 3n 1 2n 1 
 4n2 3n 1 4n2 3n 1 3 7
 lim 1 lim 1 1 . 
 2 2 2 4
 4n 3n 1 2n 2 3 1 
 n 4 2n
 n n2 c). lim 1 n2 n4 3n 1 1 lim n2 n4 3n 1 
 4 4
 n n 3n 1 3n 1
 1 lim 1 lim 
 2 4
 n n 3n 1 2 4 3 1 
 n n 1 
 n3 n4 
 1 
 n 3 
 n 3
 1 lim 1 lim 1 0 1. 
 3 1 n
 n2 1 1 
 2 4 
 n n 
 n n 1 n 
d). lim n n 1 n lim 
 n 1 n
 n n n
 lim lim lim . 
 1 1 2
 n 1 n n 1 1 
 n n 
Câu 10: Tìm các giới hạn sau:
a). lim 3 n 2 3 n b). lim 3 n n3 n 2 
c). lim 3 2n n3 n 1 d). lim 3 n3 2n2 n 1 
 LỜI GIẢI
 n 2 n
a). lim 3 n 2 3 n lim 
 2 2
 3 n 2 3 n 2.3 n 3 n 
 2
 lim 2
 2
 2 2 3 3
 3 n 1 3 n 1 . n n
 n n 
 2 2
 lim lim 0. 
 2 2
 3
 2 2 2 3 n
 3 n 3 1 3 1 1 
 n n 
b). lim 3 n n3 n 2 lim 3 n n3 n 2 
 n n3 n3 n
 lim 2 2 lim 2 2
 3 3 3 3 2 
 n n n n .n n 3 1 3 1 2
 3 n 1 3 n 1 .n n
 2 2 
 n n n 1
 lim 2 lim 2 0 2 2. 
 2 3n
 2 1
 n2 3 1 3 1 1 
 n2 n2 
c). lim 3 2n n3 n 1 lim 3 2n n3 n 1 
 2n n3 n3
 lim 2 1
 3 2n n3 3 2n n3 .n n2
 2n
 lim 3 1
 3 2 3 2 2
 3 n 1 3 n 1 .n n
 2 2 
 n n 
 2n 2
 lim 1 lim 1 0 1 1. 
 2 3n
 2 2
 n2 3 1 3 1 1 
 n2 n2 
d) lim 3 n3 2n2 n 1 lim 3 n3 2n2 n 1 
 n3 2n2 n3
 lim 2 1
 3 n3 2n 3 n3 2n.n n2
 2n2
 lim 2 1
 3 2 3 2 2
 3 n 1 n 1 .n n
 2 2 
 n n 
 2n2
 lim 1 
 2 
 2 2
 n2 3 1 3 1 1 
 n2 n2 
 2 2 1
 lim 2 1 1 .
 2 2 3 3
 3 1 3 1 13
 2 2
 n n
Câu 11: Tìm các giới hạn sau:
a). lim 3 8n3 3n2 2 5 2n b) lim 3 8n3 3n2 2 3 5n2 8n3 c)
 3 3 3 3 2 
 lim n. n n n d). lim 8n 2n 1 3 2n 
 LỜI GIẢI
a). lim 3 8n3 3n2 2 5 2n lim 3 8n3 3n2 2 2n 5 8n3 3n2 2 8n3
 lim 2 5
 3 8n3 3n2 2 3 8n3 3n2 2.2n 4n2
 3n2 2
 lim 2 5
 3 3 2 3 3 2 2
 3 n 8 n 8 .2n 4n
 3 3 
 n n n n 
 2 2 
 n 3 
 n2 
 lim 5 
 2 
 3 2 3 2
 n2 3 8 3 8 .2 4 
 n n3 n n3 
 2
 3 
 2 3 1 21
 lim n 5 5 5 . 
 3 2 3 2 4 4 4 4 4
 3 8 3 8 .2 4
 2 3
 n n n n
b). lim 3 8n3 3n2 2 3 5n2 8n3 
 8n3 3n2 2 5n2 8n3
 lim 2 2
 3 8n3 3n2 2 3 8n3 3n2 2.3 5n2 8n3 3 5n2 8n3 
 2
= 8n 2 
 lim 2 2
 3 3 2 3 3 2 3 5 3 5 
 3 n 8 3 n 8 5 n 8 3 n 8 
 3 3 
 n n n n n n 
 2 2 
 n 8 
 n2 
 lim 
 2 3 
 3 2 3 2 5 5 
 n2 3 8 3 8 .3 8 3 8 
 n n2 n n3 n n 
 2
 8 
 2 8 2
 lim n . 
 2 3 
 3 2 3 2 5 5 4 4 4 3
 3 8 3 8 .3 8 3 8 
 2 3 
 n n n n n n 
 n n3 n n3 
c) lim n. 3 n3 n n lim 
 2
 3 n3 n 3 n3 n.n n2
 n2
 lim 2
 3 2 3 1 2
 3 n 1 3 n 1 .n n
 2 2 
 n n